Вопросы к государственному экзамену
«Дискретная математика»
1. Основные комбинаторные конфигурации: размещения, сочетания, перестановки. Соединения с повторениями. Основные правила комбинаторики. 2
2. Деревья. Задачи о кратчайших расстояниях на графах. Основные алгоритмы для решения задач о кратчайших расстояниях. 4
3. Сеть. Поток в сети. Задача о максимальном потоке в сети. Алгоритм нахождения максимального потока. 6
4. Основные понятия теории графов: граф, способы задания, маршруты, связность, расстояния в графах, степени вершины. 8
Основные комбинаторные конфигурации: размещения, сочетания, перестановки. Соединения с повторениями. Основные правила комбинаторики.
В простейших комбинаторных задачах требуется подсчитать число способов выбрать k элементов из n –элементного множества. То, что получается в результате выбора, называется выборкой из n по k или (n, k)–выборкой.
Понятие выборки отличается от понятия подмножества:
1. в выборках может допускаться повторение элементов.
2. выборки могут быть упорядоченными или неупорядоченными. Упорядоченность означает, что выборки, состоящие из одних и тех же элементов, но расположенных в разном порядке, считаются различными.
Пусть - какое-либо конечное множество. Соединением элементов из множества М называется любой набор, составленный из элементов множества М.
Если в этом наборе какой-либо элемент встречается больше, чем один раз то говорят о соединениис повторениями; если же в наборе каждый элемент появляется лишь один раз, то говорят о соединении без повторений.
· 
Перестановкой элементов множества М называется всякое соединение элементов множества М, в котором обязательно присутствуют все элементы из М и в котором учитывается порядок следования элементов друг за другом. При произвольном n количество Pn всевозможных перестановок множества
равно
· Всякое соединение из k элементов множества, в котором учитывается порядок следования элементов друг за другом, называется размещением из n элементов по k.
При n=k – это перестановка.
При n>k количество размещений из n по k равно:
Очевидно, что
· 
Всякое соединение из k элементов множества, где в котором порядок следования элементов друг за другом не учитывается, называется сочетанием из n по k. Количество сочетаний из n по k определяется следующей формулой:
· 
Размещение с повторениями из n элементов множества M по k - всякая конечная последовательность, состоящая из k членов данного множества M (при этом элементы в последовательности могут повторяться). Два размещения с повторениями считаются различными, если хотя бы на одном месте они имеют различные элементы множества М. Число k-размещений с повторениями равно
· Общая формулировка задач на сочетания с повторениями: имеются предметы n различных типов. Сколько k-комбинаций можно сделать из них, если не принимать во внимание порядок элементов в комбинации? Общее количество выборок в схеме выбора k элементов из n с возвращением и без учета порядка определяется формулой
 |
· 
Задачи на перестановки с повторениями: Имеются предметы k различных типов. Сколько перестановок можно сделать из n1 элементов первого типа, n2 элементов второго типа,…, nk элементов k-го типа?
Очень многие комбинаторные задачи решаются применением трех простых правил: равенства, суммы и произведения.
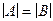
Правило равенства. Если между конечными множествами A и B есть взаимно однозначное соответствие, то
Правило суммы. Если A и B – конечные множества и то
Правило произведения. Для любых конечных множеств A и B имеет место равенство:
Первые два правила очевидны, третье следует из того, что при каждый элемент множества A образует b пар с различными элементами множества B, поэтому,
если, то всего будет пар.
Правила суммы и произведения обобщаются на случай любого числа слагаемых или сомножителей.
Для правила суммы обобщение очевидно: мощность объединения любого числа попарно непересекающихся множеств равна сумме их мощностей.
Иногда множество, из которого выбирается xi, зависит от того, какие элементы были выбраны в качестве, но число элементов в этом множестве, т.е. число вариантов для выбора остается постоянным. В этом случае правило произведения также применимо, но в более общей формулировке.
Общее правило произведения. Пусть упорядоченный набор формируется в результате последовательного выбора элементов, причем для любого и любых элемент можно выбрать способами.
Тогда весь набор может быть выбран способами.
