Задание 1: Максимально упростить выражения, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравнить ваше упрощённое выражение с исходным.

Решение:

Чтобы проверить правильность упрощения составим таблицы истинности для исходного и конечного выражений:

| a | b | c | d | 
| 
| 
| 
| 
| 
| 
| 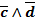
| 
|

Задание 2: Аналитическим способом, т. е. на основе формул взаимосвязи между логическими операциями, докажите справедливость ниже приведенных тождеств, представьте одно из выражений, предварительно его упростив, в базисе элементарных функций. В наборе должны фигурировать цифры вашего варианта. Недостающие функции отбираются на основе теории классов.

Решение:






Диаграммы Эйлера-Венна.
Левая часть Правая часть

Из диаграммы Эйлера-Венна видим, что тождество

справедливо.
Представим выражение  в базисе
в базисе  :
:
 .
.
Задание 3: Воспользовавшись таблицами истинности, представьте логические выражения вашего варианта двух последних заданий в СПНФ. Затем произведите минимизацию методом карт Карно (результаты расчета проверьте с помощью таблиц истинности). Наконец, определите, к каким классам (P0, P1, S, M, L) относятся ваши логические выражения.
Решение:
Рассмотрим первую формулу: F= 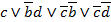
Построим по ней карту Карно:
| I SFwmlq6Vpqk0nRDQGxcGiKvXmLaicbom2wq/fp52gJNlv6fn7xXryfXqQGPoPBtYzBNQxLW3HTcG 3t+quxWoEJEt9p7JwA8FWJfXVwXm1h/5lQ6b2CgJ4ZCjgTbGIdc61C05DHM/EIv25UeHUdax0XbE o4S7XqdJstQOO5YPLQ702FL9vdk7A6H6oF31O6tnyWfWeEp3Ty/PaMztzfRwDyrSFP/McMYXdCiF aev3bIPqDWTpUpwyFxmos56spMr2ctBlof8XKE8AAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+ AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAA ACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAA ACEAh4wE0IsCAABjBQAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYA CAAAACEAzv0LONwAAAAIAQAADwAAAAAAAAAAAAAAAADlBAAAZHJzL2Rvd25yZXYueG1sUEsFBgAA AAAEAAQA8wAAAO4FAAAAAA== "/> | d | c | ||
| b | ||||
| a |
Произведя склеивание получим следующий результат в ДНФ:

Проверим получившийся результат с помощью таблицы истинности:
| a | b | c | d | F | 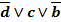
|
Представим данное выражение в СПНФ:
F= 
1. Установим, относится ли функция к классу Р0:
F(0,0,0,0)=1, таким образом функция не относится к классу Р0.
2. Установим, относится ли функция к классу Р1:
F(1,1,1,1)=1, таким образом функция относится к классу Р1.
3. Установим, относится ли функция к классу S, проверим это с помощью таблицы истинности:
| a | b | c | d | 
| 
| 
| 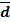
| 
| 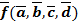
| 
|
Т. о. функция не относится к классу S, т. к. 
4. Установим, относится ли функция к классу M:

Как видно из приведенной выше таблицы данное условие не выполняется, то есть данная функция не относится к классу М.
5.Установим, относится ли функция к классу L, для этого определим все коэффициенты с0, сi  {0,1},
{0,1}, 
С0=f(0,0,0,0)=1
C1=f(1,0,0,0)=1
C2=f(0,1,0,0)=1
C3=f(0,0,1,0)=1
C4=f(0,0,0,1)=1
 =
= 
Построим таблицу истинности:
| a | b | c | d | 
| 
|
Таким образом, данная функция не относится к классу L, т. к.  и
и  не совпадают.
не совпадают.
В итоге получаем, что данная функция относится к классу функций, сохраняющих константу единица (Р1).
Рассмотрим вторую формулу: f= 
Составим таблицу истинности для данной функции:
| a | b | c | d | 
|
Построим для нее карту Карно:
| d | c | |||
| b | ||||
| a |
Произведем склейку функции. Получим следующий результат в ДНФ:
 . В результате получили функцию, совпадающую с исходной.
. В результате получили функцию, совпадающую с исходной.
Представим данное выражение в СПНФ:
F=  =
= 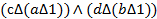
1. Установим, относится ли функция к классу Р0:
F(0,0,0,0)=1, таким образом функция не относится к классу Р0.
2. Установим, относится ли функция к классу Р1:
f(1,1,1,1)=1, таким образом функция не относится к классу Р1.
3.Установим, относится ли функция к классу S, проверим это с помощью таблицы истинности:
| a | b | c | d | 
| 
| 
| 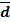
| 
| 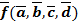
| 
|
Т. о. функция не относится к классу S, т. к. 
4. Установим, относится ли функция к классу M:

Как видно из приведенной выше таблицы данное условие не выполняется, то есть данная функция не относится к классу М.
5.Установим, относится ли функция к классу L, для этого определим все коэффициенты с0, сi  {0,1},
{0,1}, 
С0=f(0,0,0,0)=1
C1=f(1,0,0,0)=0
C2=f(0,1,0,0)=0
C3=f(0,0,1,0)=1
C4=f(0,0,0,1)=1
 =
= 
Построим таблицу истинности:
| a | b | c | d | 
| 
|
Таким образом, данная функция не относится к классу L, т. к.  и
и  не совпадают.
не совпадают.
В итоге получаем, что данная функция относится к классам функций, сохраняющих константу 1(Р1).
Задание 4:Докажите аналитическим путем справедливость трех предложенных выражений в каждом варианте.

Решение:
1) 

Левая и правая части тождества равны, значит тождество верно.
2) 

Левая и правая части тождества равны, значит тождество верно.
3) 
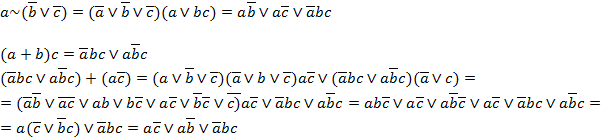
Левая и правая части тождества не равны, значит тождество неверно.
Задание 5:Ниже приведена диаграмма Эйлера- Венна. Представить заштрихованные и отдельно не заштрихованные области максимально компактными аналитическими выражениями, в которых бы использовалось минимальное количество логических операций и букв. С этой целью сначала выразить все заштрихованные области через конституенты - конъюнкты, а не заштрихованные через конституенты – дизъюнкты, и после этого приступить к упрощению совершенных форм (результаты проверить на таблицах истинности).

Выразим все заштрихованные области:

Перейдем к конъюнкторам и дизъюнкторам:

Для минимизации заштрихованной части строим карту Карно:
| A | B | C | D | 
|
| d | c | |||
| b | ||||
| a |
В итоге получаем минимальное представление: 
Окончательное решение: 
Выразим все не заштрихованные области:

| A | B | C | D | 
| 
| 
| 
| 
|
| d | c | |||
| b | ||||
| a |
В итоге получаем минимальное представление: 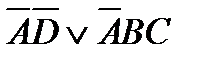
Окончательное решение:  .
.






