Курсовая работа Задание №3 Вариант №2
МЕХАНИЗМ КАЧАЮЩЕГОСЯ ПИТАНИЯ
Механизм качающегося питателя – кривошипно-ползуный механизм- состоит из кривошипа 2, шатуна 3 и ползуна (каретки) 4. Кривошип 2 (коленчатый вал, эксцентрированый вал) получает вращение от электродвигателя 2 через плоскоременную передачу 6, двухступенчатый редуктор 5 и компенсирующую муфту 7. Кривошип через шатун 3 приводит в возвратно- поступательное движения ползун 4. Ползун представляет собой каретку, перекрывающею выпускное отверстие бункера угла. Каретка (ползун) перемещается по направляющей на катках. При возвратно-поступательном движении каретка часть угла, лежащая на каретки, сталкивается давлением угля в бункере на конвейер. Качающейся питатель обеспечивает перекрытие выпускного отверстия бункера и равномерно подачу угля на конвейер.
Включение питателя сблокировано с конвейером. Для предотвращения завала конвейера включение питателя производится после включения конвейера. При перемещении пот направляющим каретка преодолевает сопротивление смещение слоев угля в горловине бункера. Диаграмма сил сопротивления при движении каретки «вперед» и «назад» представлена на рисунке в задании.
| Параметры | Обозначение | Ед. измерения | Вариант 2 |
| Частота вращения | Об/мин | ||
| Длина кривошипа | мм | ||
| Длина шатуна | мм | ||
| Положение ЦМ шатуна | мм | ||
| Положение ЦМ ползуна | мм | ||
| Масса шатуна | кг | ||
| Масса ползуна | кг | ||
| Момент инерции шатуна | кгм | ||
| Момент инерции ползуна | кгм | ||
| Максимальное сопротивление | н | ||
| Срок службы | час |
2.1 Кинематический расчет механизма.
2.1.1 Структурный анализ механизма.
Механизм (рис. 2.1) состоит из кривошипа 2, шатуна 3, ползуна 4 и стойки 1.
Рис 2.1.
Заданный механизм- центральный кривошипно- ползунный.
Звенья механизма образуют кинематические пары 5- го класса:
вращательные 1-2; 2-3; 3-4.
поступательную 4-1.
Степень подвижности механизма определим по формуле Чебышева W= 3п-2Р3-Р4 = 3*3-2*4-0=1,
где: п=3- число подвижных звеньев
Р3=4 и Р4=0- число кинематических пар 5- го и 4-го классов.
Выделим из механизма группу звеньев 3-4- это группа Ассура II класса, II порядка, II вида (рис. 2.2).
Рис. 2.2
Оставшиеся звенья 1 и 2 образуют механизм I класса (рис. 2.3).
Рис. 2.3
По классификации Ассура- Артоболевского механизм относится ко II классу.
Структурная формула механизма:
I (1,2) → II (3,4)
2.1.2 Построим в масштабе μс= 0,002 м/мм план положения механизма. Разбиваем траекторию т. А на 12 равных частей. При помощи засечек находим 12 положений точки В. Положение 2 выдилим жирными линиями. Покажем на пол. 2 центры масс (ЦМ) звеньев 3 и 4. 2.1.2. Построим в масштабе  м/мм график перемещения т. В координаты графика замеряем (с учетом масштаба) с плана положения механизма.
м/мм график перемещения т. В координаты графика замеряем (с учетом масштаба) с плана положения механизма.
Определим масштаб оси абсцисс.
Период движения механизма.

Принимаем, что период Т соответствует отрезок оси абсцисс длиной L=180 мм.
Масштаб оси абсцисс:
по времени 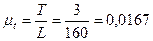 с/мм
с/мм
по углам поворота кривошипа 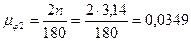 рад/мм.
рад/мм.
Обводим координаты точек главной кривой перемещения определим скорость т.В в различных положениях. Используем метод хорд. Из точки Р, находящейся на расстоянии Н=50мм от начала координат проводим лучи параллельно хордам каждого участка кривой  .
.
Точки пересечения лучей с осью ординат переносим на середины соответствующих участков и обводим плавной кривой скорости т.В  .
.
Масштаб скорости

Заменим ординаты скоростей для каждого положения и с учетом масштаба составим табл.2.1.
Табл.2.1
| Пол. | |||||||||||||
| Vв м/с | 0,044 | 0,087 | 0,11 | 0,103 | 0,06 | -0,06 | -0,103 | -0,11 | -0,087 | -0,044 |
2.1.5. Построим для полож.2 план скоростей по векторному уравнению

Модуль скорости т.А
 м/с
м/с
Где  -угловая скорость кривошипа
-угловая скорость кривошипа
 мм.
мм.
Из т.А проводим ┴ АВ линию до пересечения из полюса Р горизонтально (направление движение т.В). Точку пересечения В соединяем с полюсом.
Для определения скорости точки S3 используем геометрическое подобие.
Так как отношение  то на плане скоростей делим отрезок АВ точкою S3 в такой же пропорции.
то на плане скоростей делим отрезок АВ точкою S3 в такой же пропорции.
Значит,
 мм.
мм.
Точку S3 соединим с полюсом.
Из плана скоростей находим для пол.2
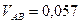 м/с;
м/с;  м/с;
м/с; 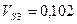 м/с;
м/с;
Сравним для положения 2 величину полученную при помощи графика и плана скоростей.
Разница составляет

Что допустимо, так как меньше 5%.
Определим для пол.2 угловую скорость звена 3.
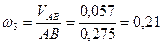 рад/с.
рад/с.
Для определения направления  поместим вектор
поместим вектор 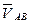 в точку В плана положения и наблюдаем, в какую сторону вращается т.В вокруг т.А.
в точку В плана положения и наблюдаем, в какую сторону вращается т.В вокруг т.А.
2.1.6. Построим ля положения 2 план ускорений в масштабе 
Ускорение т.А вследствие того, что 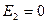

Модуль ускарения
 м/c
м/c
Ускорение т. В находим из уровнения
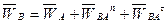
Модуль нормального ускорения
 м/с2
м/с2
Из полюса Ри проводим //ОА в направлении от А к О вектор  , изображающий в масштабе
, изображающий в масштабе  . Длина вектора
. Длина вектора
 мм.
мм.
Из точки А проводим параллельно АВ в направлении от В к А вектор аn, изображающий в масштабе ускорение  . Из точки n проводим перпендикулярно АВ направление ускорение
. Из точки n проводим перпендикулярно АВ направление ускорение  до пересечения с точкой В с горизонтальной линией, проведенной из полюса.
до пересечения с точкой В с горизонтальной линией, проведенной из полюса.
Вектор  изображает ускорение
изображает ускорение  .
.
Ускорение т. S3 находим из геометрического подобия. Значит на плане ускорений  мм.
мм.
Из плана ускорений находим:  м/с2;
м/с2;  м/с2;
м/с2;  м/с2.
м/с2.
Угловое ускорение шатуна 3, совершающего плоское движение
 рад/с2.
рад/с2.
Для определения направления  поместим вектор
поместим вектор  в т.В плана положения и наблюдаем, в какую сторону вращается т.В вокруг т.Аю
в т.В плана положения и наблюдаем, в какую сторону вращается т.В вокруг т.Аю
СИЛОВОЙ РАСЧЕТ МЕХАНИЗМА.
2.2.1. Построим в масштабе µр=50 н/мм график сил полезного сопротивления.
По данным графика составим табл.2.2.
Табл. 2.2.
| Пол. | |||||||||||||
| Р, Н |
2.2.2. Силы, действующие на звенья механизма в пол.2.
Сила полезного сопротивления Рnc=5200 Нм
Определим силы тяжести звеньев G=m.g
где: g=10 м/с- ускорение силы тяжести
G3=m3.g=17.10=170 Н;
G4=m4.g=20.10=200 Н;
Силы инерции звеньев 
Знак «минус» показывает, что сила инерции направления противоположно ускорению.
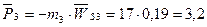 н
н
 н
н
Момент силы инерции звена 3 
Знак «минус» показывает, что 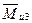 противоположно ускорению
противоположно ускорению  .
.
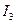 - момент инерции звена 3 относительно оси проходящей через точку S3.
- момент инерции звена 3 относительно оси проходящей через точку S3.
 кг/м, тогда
кг/м, тогда  Нм.
Нм.
2.2.3. Выделим из механизма группу Ассура (звенья 2и3), приложим к точкам звеньев силы тяжести, инерции, полезного сопротивления и реакции отброшенных звеньев. Реакция 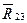 разложим на 2 взаимно-перпендикулярные составляющие
разложим на 2 взаимно-перпендикулярные составляющие  и
и  .
.
Рассмотрим группу в равновесии, что мы имеем право делать по принципу Даламбера: если к движущейся системе кроме внешних сил приложить силы инерции, то систему можно рассматривать в равновесии.
 ;
; 
Построим в масштабе µр=20 Н/мм план сил группы звеньев 3 и 4. При построении плана сил из-за небольшой величины силы  и
и 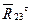 не учитываем. План сил- замкнутый многоугольник, у которого начало последующего вектора находится в конце предидущего.
не учитываем. План сил- замкнутый многоугольник, у которого начало последующего вектора находится в конце предидущего.
План сил строим по векторному уравнению

Из плана сил находим
 Н;
Н;  Н.
Н.
Определим место положения реакции  .
.
Для этого рассмотрим в равновесии звено 4
 ;
; 
 мм.
мм.
2.2.4. Определим уравновешивающую силу
 ;
; 
 Н.
Н.
2.2.5. определим реакцию в шарнире В из векторного уравнения

На плане сил группы Асоура (покажем пунктиром) находим
 к
к
2.2.6. Определим реакцию в масштабе µр=50 Н/мм план сил кривошипа по уравнению 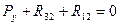
Из плана сил находим  н.
н.






