Определители
1.1 Свойства определителей
Определителем или детерминантом n-го порядка называется число, записываемое в виде
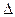 [1]
[1] 
и вычисляемое по данным числам 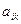 (действительным или комплексным) – элементам определителя – по следующему закону:
(действительным или комплексным) – элементам определителя – по следующему закону:
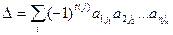 ,
,
распространенная на всевозможные различные перестановки 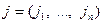 из чисел
из чисел 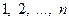 . Число
. Число 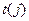 равно числу транспозиций, которые нужно сделать, чтобы перейти от основной перестановки
равно числу транспозиций, которые нужно сделать, чтобы перейти от основной перестановки 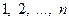 к перестановке n -го порядка
к перестановке n -го порядка 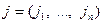 . Произведение
. Произведение  называется членом определителя.
называется членом определителя.
Определители n-го порядка удовлетворяют свойствам:
а) Величина определителя не меняется, если у него заменить строки соответствующими столбцами;
б) Величина определителя меняет знак, если у него переменить местами строки (столбцы);
в) Величина определителя умножается на число k (действительное или комплексное), если элементы какого-либо его столбца или строки умножить на k (т.е. множитель, присутствующий с строке или столбце, можно выносить за знак определителя);
г) Величина определителя равна 0, если элементы какого-либо его столбца или строки равны нулю;
д) Величина определителя равна 0, если элементы двух строк или столбцов соответственно равны;
е) Сумма произведений элементов 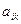 некоторой строки (столбца) определителя на алгебраические дополнения этих элементов равна величине определителя (см. п.1.2 Разложение определителя по строке и столбцу);
некоторой строки (столбца) определителя на алгебраические дополнения этих элементов равна величине определителя (см. п.1.2 Разложение определителя по строке и столбцу);
ж) Сумма произведений элементов 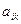 некоторой строки (столбца) определителя на соответствующие адъюнкты (алгебраические дополнения) элементов другой строки (столбца) равна нулю:
некоторой строки (столбца) определителя на соответствующие адъюнкты (алгебраические дополнения) элементов другой строки (столбца) равна нулю:
 ,
,  ;
;
з) Пусть даны два определителя n -го порядка  и
и  , у которых все строки (столбцы) одинаковы, кроме определенной одной (одного). Сумма таких определителей равна определителю
, у которых все строки (столбцы) одинаковы, кроме определенной одной (одного). Сумма таких определителей равна определителю 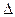 n -го порядка, у которого указанная строка (столбец) состоит из суммы соответствующих элементов этой строки (столбца) определителей
n -го порядка, у которого указанная строка (столбец) состоит из суммы соответствующих элементов этой строки (столбца) определителей  и
и  ;
;
и) Величина определителя не изменится, если к элементам какой-либо его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на число k;
к) Пусть  ,
,  . Произведение двух определителей n -го порядка с элементами
. Произведение двух определителей n -го порядка с элементами 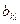 и
и 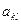 есть в свою очередь определитель n -го порядка с элементами
есть в свою очередь определитель n -го порядка с элементами 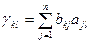 , т.е.
, т.е.

1.2 Разложение определителя по строке и столбцу
Возьмем определитель n -го порядка:
 .
.
Вычеркнем из этого определителя i -ую строку и k -ый столбец. Оставшееся выражение порождает определитель (n-1)-го порядка 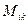 , называемый минором элемента
, называемый минором элемента 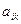 . Величина же
. Величина же 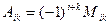 называется алгебраическим дополнением или адъюнктом элемента
называется алгебраическим дополнением или адъюнктом элемента 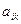 .
.
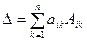
 - разложение определителя по элементам i -ой строки,
- разложение определителя по элементам i -ой строки,
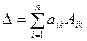
 - разложение определителя по элементам k -го столбца;
- разложение определителя по элементам k -го столбца;
Определитель
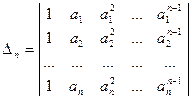 ,
,
порожденный числами  называется степенным или определителем Вандермонда [2]. Определитель Вандермонда будет равен нулю, если среди чисел
называется степенным или определителем Вандермонда [2]. Определитель Вандермонда будет равен нулю, если среди чисел  есть одинаковые.
есть одинаковые.
Правило Крамера [3]. Зададим систему или n линейных уравнений с n неизвестными
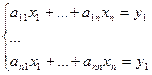 .
.
Числа 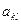 (действительные или комплексные), называемые коэффициентами системы, заданы. Можно говорить, что система определяется матрицей
(действительные или комплексные), называемые коэффициентами системы, заданы. Можно говорить, что система определяется матрицей
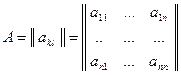
ее коэффициентов.
Если определитель данной системы не равен 0, т.е. 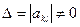 , то система имеет единственное решение для любого вектора y, вычисляемое по формуле Крамера
, то система имеет единственное решение для любого вектора y, вычисляемое по формуле Крамера 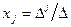
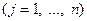 , где
, где  - определитель, получаемый из определителя
- определитель, получаемый из определителя 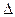 , если в нем заменить числа j -го столба соответственно на числа
, если в нем заменить числа j -го столба соответственно на числа 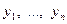 :
:
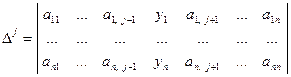 .
.
Таким образом 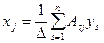
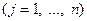 , где
, где 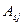 - адъюнкт элемента
- адъюнкт элемента 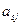 в определителе
в определителе 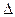 .
.
2. Комплексные числа
2.1 Понятие комплексного числа
Комплексными числами называются упорядоченные пары 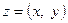 действительных чисел. Выражения
действительных чисел. Выражения  – алгебраическая форма к.ч., где
– алгебраическая форма к.ч., где 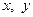 - действительные числа, а
- действительные числа, а 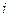 - специальный символ; при этом для комплексных чисел
- специальный символ; при этом для комплексных чисел  ,
, 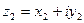 введены понятия равенства и арифметические операции по следующим правилам:
введены понятия равенства и арифметические операции по следующим правилам:
1) 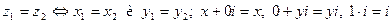 ;
;
2) 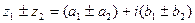 ;
;
3) 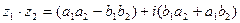 ;
;
4) 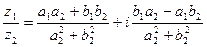
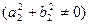 .
.
Из 1) и 3) следует, что 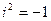 .
.
Таким образом, введенные операции сложения и умножения обладают свойствами:
1) коммутативности 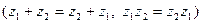 ;
;
2) ассоциативности 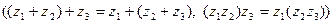 ;
;
3) дистрибутивности 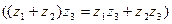 ;
;
4)  ;
;
5) 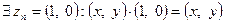 ;
;
6)  ;
;
7) 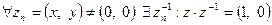 .
.
Если на плоскость введена декартовая прямоугольная система координат 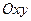 , то всякому комплексному числу
, то всякому комплексному числу 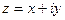 может быть поставлена в соответствие некоторая точка
может быть поставлена в соответствие некоторая точка  с абсциссой x и ординатой y. При этом говорят, что точка
с абсциссой x и ординатой y. При этом говорят, что точка  изображает к.ч.
изображает к.ч. 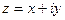 . Плоскость, на которой изображаются к.ч., называется комплексной плоскостью. Ось
. Плоскость, на которой изображаются к.ч., называется комплексной плоскостью. Ось 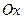 – действительной осью, а ось
– действительной осью, а ось  – мнимой осью.
– мнимой осью.
Число  называется модулем к.ч.
называется модулем к.ч. 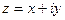 и обозначается символом
и обозначается символом  . Модуль числа z равен расстоянию от начала координат до точки M, изображающей это число.
. Модуль числа z равен расстоянию от начала координат до точки M, изображающей это число.
Всякое решение 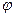 системы уравнений
системы уравнений
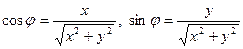 (*)
(*)
называется аргументом к.ч. 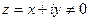 . Все аргументы числа z различаются на целые кратные
. Все аргументы числа z различаются на целые кратные  и обозначаются единым символом
и обозначаются единым символом  .Каждое значение аргумента совпадает с величиной
.Каждое значение аргумента совпадает с величиной 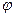 некоторого угла, на который следует повернуть ось
некоторого угла, на который следует повернуть ось 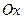 до совпадения с радиус-вектором
до совпадения с радиус-вектором 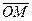 точки M (при этом
точки M (при этом 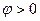 , если поворот совершается против часовой стрелки, и
, если поворот совершается против часовой стрелки, и 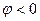 в противном случае). Значение
в противном случае). Значение  , удовлетворяющее условию
, удовлетворяющее условию 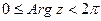 , называется главным значением аргумента и обозначается символом
, называется главным значением аргумента и обозначается символом 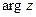 . В некоторых случаях главным значением аргумента называется значение
. В некоторых случаях главным значением аргумента называется значение  , удовлетворяющее условию
, удовлетворяющее условию  .
.
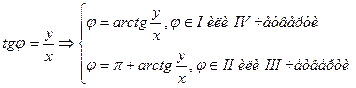 .
.
Из соотношений (*) следует, что для всякого к.ч. z справедливо равенство
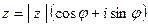 ,
,
называемое тригонометрической формой числа z.
Для к.ч. 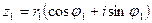 и
и  в тригонометрической форме, где
в тригонометрической форме, где 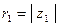 и
и 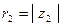 , справедливы равенства:
, справедливы равенства:
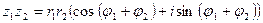 ,
,
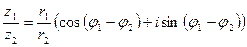 .
.
2.2 Комплексные числа в показательной форме
Пусть 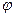 - произвольное действительное число. Символом
- произвольное действительное число. Символом 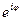 обозначается комплексное число
обозначается комплексное число 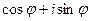 . С помощью этого обозначения всякое к.ч.
. С помощью этого обозначения всякое к.ч. 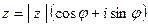 может быть записано в показательной форме
может быть записано в показательной форме
 .
.
Формулы Эйлера:

Для к.ч. 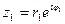 и
и 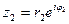 в показательной форме, где
в показательной форме, где 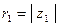 и
и 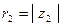 , справедливы равенства:
, справедливы равенства:
 ,
,
 ,
,
 ,
,

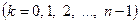 .
.
Число 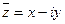 называется сопряженным к комплексному числу
называется сопряженным к комплексному числу 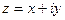 . Очевидно, что
. Очевидно, что 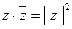 .
.
Операция построения сопряженного к.ч. обладает следующими простыми свойствами:
 ,
,  ,
, 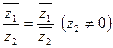 .
.
Формула Муавра:
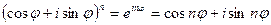 .
.
2.3 Разложение многочленов на множители
Многочленом n -ой степени называется функция вида
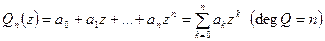 ,
,
где 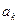 – постоянные коэффициенты (действительные или комплексные), а
– постоянные коэффициенты (действительные или комплексные), а 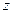 – комплексная переменная, которая может принимать любые комплексные значения
– комплексная переменная, которая может принимать любые комплексные значения 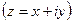 или, выражаясь геометрическим языком,
или, выражаясь геометрическим языком, 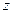 может быть любой точкой комплексной плоскости.
может быть любой точкой комплексной плоскости.
Если 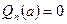 при
при  , то число
, то число 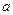 называется корнем или нулем многочлена
называется корнем или нулем многочлена 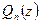 .
.
Для многочленов определены следующие арифметические операции:
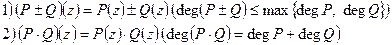
В результате операций 1) и 2) снова получится многочлен. Частное двух многочленов может не быть многочленом.
Деление многочленов с остатком.
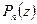 ,
, 
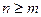
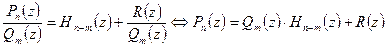 ,
,
где 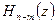 – частное, а
– частное, а  – остаток.
– остаток.
Теорема Безу.
Для того, чтобы многочлен 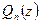 имел (комплексный) корень
имел (комплексный) корень 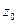 , необходимо и достаточно, чтобы он делился на
, необходимо и достаточно, чтобы он делился на 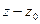 , т.е. чтобы его можно было представить в виде произведения
, т.е. чтобы его можно было представить в виде произведения 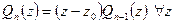 , где
, где  – некоторый многочлен степени n-1.
– некоторый многочлен степени n-1.
Если при разложении 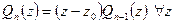
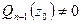 , то на основании теоремы Безу применимой к
, то на основании теоремы Безу применимой к 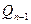 , многочлен
, многочлен  не делится на
не делится на 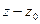 , а
, а 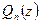 хотя и делится на
хотя и делится на 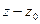 , но не делится на
, но не делится на  . В этом случае говорят, что
. В этом случае говорят, что 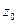 – простой корень (нуль) многочлена
– простой корень (нуль) многочлена 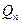 .
.
Пусть теперь  . Тогда по теореме Безу, применимой к
. Тогда по теореме Безу, применимой к 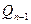 , многочлен
, многочлен  делится на
делится на 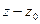 , и мы получим
, и мы получим  , где
, где 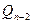 – некоторый многочлен степени n-2. Если
– некоторый многочлен степени n-2. Если 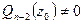 , то
, то 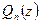 делится на
делится на  , но не делится на
, но не делится на 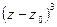 , и тогда число
, и тогда число 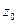 называется корнем (нулем) кратности 2.
называется корнем (нулем) кратности 2.
В общем случае для некоторого натурального 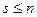 имеет место
имеет место
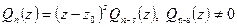 ,
,
где 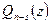 – многочлен степени n-s, и тогда говорят, что
– многочлен степени n-s, и тогда говорят, что 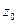 – корень (нуль) многочлена
– корень (нуль) многочлена 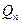 кратности s.
кратности s.
Теорема Гаусса (основная теорема алгебры).
Всякий многочлен n -ой степени (ненулевой, т.е. 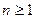 ) имеет по крайней мере один комплексный корень (нуль).
) имеет по крайней мере один комплексный корень (нуль).
Следствие из теоремы Гаусса.
Многочлен n -ой степени 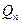 со старшим не равным нулю коэффициентом
со старшим не равным нулю коэффициентом  имеет n комплексных корней с учетом кратности, иначе говоря
имеет n комплексных корней с учетом кратности, иначе говоря 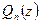 представляется в виде произведения
представляется в виде произведения
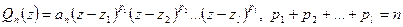 ,
,
где  – различные корни
– различные корни 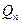 кратностей, соответственно
кратностей, соответственно 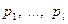 .
.
Если у многочлена с вещественными коэффициентами есть комплексные корни, то они входят сопряженными парами, т.е. если 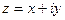 – корень многочлена
– корень многочлена 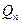 , то и корень
, то и корень 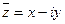 будет являться корнем многочлена
будет являться корнем многочлена 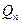 .
.
Раскладывая в разложении на квадратичные множители многочлена 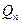 комплексные корни
комплексные корни  на сопряженные, т.е.
на сопряженные, т.е. 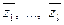 получим разложение многочлена
получим разложение многочлена 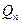 на линейные множители.
на линейные множители.
В результате получим разложение вида
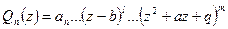 ,
,
где 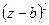 отвечает вещественному корню b кратности l, а
отвечает вещественному корню b кратности l, а 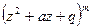 – комплексным корням
– комплексным корням 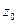 и
и 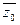 кратности m.
кратности m.
3. Алгебра матриц
3.1 Умножение матриц
Матрицей размера 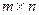 или (
или (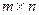 )- матрицей называется прямоугольная таблица из чисел
)- матрицей называется прямоугольная таблица из чисел 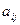 ,
,  ,
,  ,
,
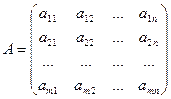 ,
,
состоящая из 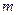 строк и
строк и 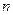 столбцов. При
столбцов. При 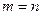 матрица называется квадратной матрицей n-ого порядка.
матрица называется квадратной матрицей n-ого порядка.
Суммой  (
(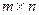 )- матриц
)- матриц 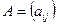 и
и 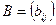 называется матрица
называется матрица 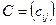 того же порядка, каждый элемент которой равен сумме соответственных элементов матриц
того же порядка, каждый элемент которой равен сумме соответственных элементов матриц 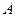 и
и 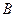 :
:
 ,
, 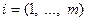 ,
,  .
.
Легко видеть, что
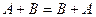 ,
,
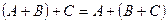 .
.
Замечание: складывать можно только матрицы одного размера.
Произведением 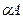 матрицы
матрицы 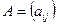 на число
на число 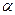 (действительное или комплексное) называется матрица
(действительное или комплексное) называется матрица 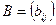 , получающаяся из матрицы
, получающаяся из матрицы 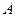 умножением всех ее элементов на
умножением всех ее элементов на 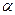 :
:
 ,
, 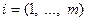 ,
,  .
.
Причем 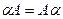 .
.
Произведением 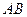
 - матрицы
- матрицы 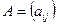 на
на  - матрицу
- матрицу 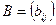 называется
называется 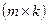 -матрица
-матрица 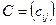 , элемент которой
, элемент которой 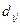 , стоящий в i -ой строке и в j -ом столбце, равен сумме произведений соответствующих элементов i -ой строки матрицы
, стоящий в i -ой строке и в j -ом столбце, равен сумме произведений соответствующих элементов i -ой строки матрицы 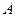 и j -ого столбца матрицы
и j -ого столбца матрицы 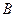 :
:
 ,
, 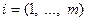 ,
, 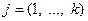 .
.
Легко видеть, что
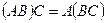 .
.
Матрицы 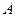 и
и 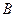 называются перестановочными (коммутирующими), если
называются перестановочными (коммутирующими), если  .
.
Свойства умножения квадратных матриц.
1) При перемножении квадратных матриц, допустим 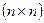 -матрицы
-матрицы 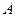 на
на 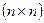 -матрицу
-матрицу 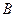 , получим
, получим 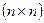 -матрицу
-матрицу 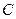 . Причем
. Причем 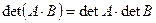 .
.
2) 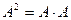 ,
, 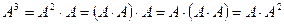 , т.е. матрица
, т.е. матрица 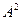 коммутирует с
коммутирует с 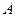 . Вообще
. Вообще  .
.
Матрица 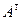 называется транспонированной к матрице
называется транспонированной к матрице 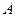 , если выполняется условие
, если выполняется условие
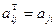
для всех  , где
, где 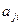 и
и  – элементы матриц
– элементы матриц 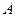 и
и 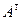 соответственно. При транспонировании квадратной матрицы ее определитель не меняется.
соответственно. При транспонировании квадратной матрицы ее определитель не меняется.
Матрица транспонированного произведения есть произведение транспонированных матриц в обратном порядке, т.е.
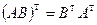 .
.
3.2 Обратная матрица
Квадратная матрица 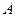 называется вырожденной (особенной), если ее определитель равен 0, и невырожденной (неособенной) в противном случае. Если
называется вырожденной (особенной), если ее определитель равен 0, и невырожденной (неособенной) в противном случае. Если 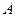 – невырожденная матрица, то существует и притом единственная матрица
– невырожденная матрица, то существует и притом единственная матрица  такая, что
такая, что
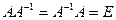 ,
,
где E – единичная матрица (т.е. такая, на главной диагонали которой стоят единицы, а все остальные элементы равны 0). Матрица  называется обратной к матрице
называется обратной к матрице 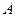 и ищется следующим образом:
и ищется следующим образом:
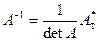 ,
,
где  – транспонированная к матрице, составленной из алгебраических дополнений соответствующих элементов матрицы
– транспонированная к матрице, составленной из алгебраических дополнений соответствующих элементов матрицы 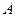 .
.
Решение матричных уравнений.
1) 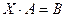
Домножив справа на  , получим
, получим
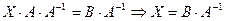 .
.
2) 
Домножив слева на  , получим
, получим
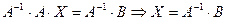 .
.
3) 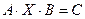
Домножив слева на  и справа на
и справа на 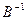 , получим
, получим
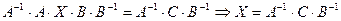 .
.
Решение систем линейных уравнений.
Дана система:
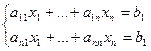 .
.
Решение:
Данная система является частным случаем матричного уравнения 2), где
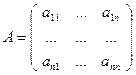 ,
, 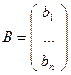 ,
, 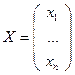 .
.
При условии, что 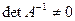 система имеет единственное решение, а именно
система имеет единственное решение, а именно
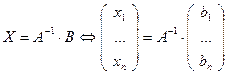 , где
, где 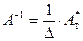 .
.
Рассмотрим теперь на примере системы:
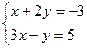 .
.
Решение:
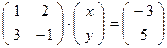 (*)
(*)
Полученное матричное уравнение имеет вид 2), т.е.  . Находим матрицу
. Находим матрицу  , обратную к матрице
, обратную к матрице 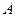 :
:
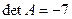 ;
; 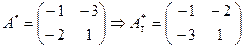

Преобразовав наше матричное уравнение (*) как описано выше в пункте 2), получим
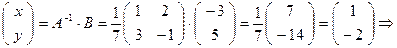
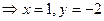
4. Линейные пространства
4.1 Понятие линейного пространства
Множество L называется линейным (векторным) пространством, если выполнены следующие условия:
1) В L введена операция сложения элементов, т.е.  определено отображение
определено отображение  (обозначение:
(обозначение:  ), обладающее следующими свойствами:
), обладающее следующими свойствами:
-  ;
;
- 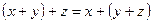 ;
;
-  (элемент 0 называется нулевым);
(элемент 0 называется нулевым);
- 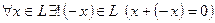 (элемент – x называется противоположным элементу x);
(элемент – x называется противоположным элементу x);
2) В L введена операция умножения элементов на действительные (комплексные) числа, т.е. 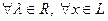 определено отображение
определено отображение 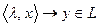 (обозначение:
(обозначение: 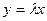 ), обладающее следующими свойствами:
), обладающее следующими свойствами:
- 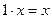 ;
;
- 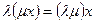 ;
;
3) Операция сложения элементов и умножения их на числа удовлетворяют законам дистрибутивности:
- 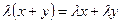 ;
;
- 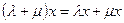 ;
;
Элементы линейного пространства называются векторами. Пространство L называется действительным, если в L операция умножения векторов на число определена только для действительных чисел, и комплексным, если эта операция определена для комплексных чисел.
Примеры линейных пространств:
1)  – пространство геометрических векторов
– пространство геометрических векторов  .
.  :
:
- если 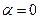 , то
, то  ;
;
- если 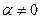 , то
, то 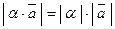 .
.
2) 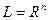 – арифметическое пространство.
– арифметическое пространство.
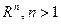 – множество упорядоченных наборов из n вещественных чисел со следующими правилами:
– множество упорядоченных наборов из n вещественных чисел со следующими правилами:
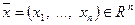 ,
, 

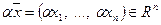 ,
, 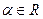
3)  – пространство многочленов.
– пространство многочленов.
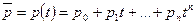 ,
, 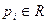
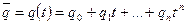 ,
, 
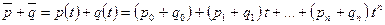
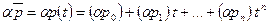
4) 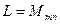 – пространство (
– пространство (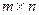 )-матриц.
)-матриц.
 (
(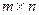 ),
),  (
(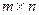 )
)
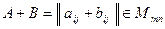

5) 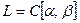 – пространство функций, непрерывных на
– пространство функций, непрерывных на  .
.
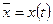 ,
, 

 ,
, 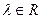
 ,
, 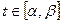
Подпространством линейного пространства L называется такое подмножество 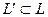 , которое обладает свойствами:
, которое обладает свойствами:
1)  ;
;
2)  .
.
Выводы:
1) всякое подпространство содержит 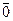 ;
;
2) каждый вектор в подпространство входит с противоположным.
Теорема 1.
Подпространство линейного пространства само является линейным пространством относительно операций сложения и умножения векторов на число.
 является линейной комбинацией векторов системы S, если
является линейной комбинацией векторов системы S, если 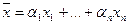 , где
, где 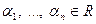 .
.
Совокупность линейных комбинаций векторов системы S из линейного пространства L называется линейной оболочкой, т.е.

Теорема 2.
Линейная оболочка 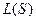 системы S в линейном пространстве L образует подпространство в L.
системы S в линейном пространстве L образует подпространство в L.
Линейная оболочка системы – наименьшее подпространство, содержащее все векторы системы.
4.2 Линейная зависимость и независимость системы векторов
Система векторов 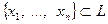 называется линейно зависимой, если найдутся числа
называется линейно зависимой, если найдутся числа 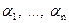 , не равные одновременно нулю и такие, что
, не равные одновременно нулю и такие, что 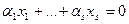 ; в противном случае эта система называется линейно независимой.
; в противном случае эта система называется линейно независимой.
Свойства:
1)  – линейно зависима, если
– линейно зависима, если 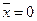 ;
;
2) 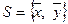 – линейно зависима, если
– линейно зависима, если 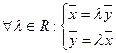 ;
;
3) Если система содержит зависимую подсистему, то вся система зависима.
Следствия:
1) Всякая часть линейно независимой системы линейно независима;
2) Система, содержащая 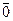 – линейно зависима;
– линейно зависима;
3) Система, содержащая два равных или пропорциональных вектора, линейно зависима.
Критерий линейной зависимости.
Для того, чтобы система векторов была линейно зависима необходимо и достаточно, чтобы хотя бы один из ее векторов линейно выражался через другие.
Геометрический смысл линейной зависимости.
1) Система из 2-х векторов линейно зависима тогда и только тогда, когда они коллинеарны, т.е.
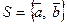 – линейно зависима, когда
– линейно зависима, когда 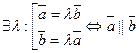 .
.
Замечание: 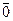 коллинеарен любому (каждому) вектору.
коллинеарен любому (каждому) вектору.
2) Система из 3-х векторов линейно зависима тогда и только тогда, когда они компланарны.
3) Любая система из 4-х и более векторов – линейно зависима.
4.3 Ранг системы векторов
Рангом системы векторов называется размерность ее линейной оболочки, т.е.
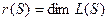 .
.
Подсистема  системы
системы 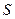 называется базой в
называется базой в 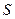 , если
, если
1)  – линейно независима;
– линейно независима;
2) Любой вектор из 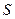 линейно выражается через векторы
линейно выражается через векторы  .
.
4.4 Сохранение ранга системы векторов при элементарных преобразованиях.
Пусть 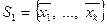 , а
, а 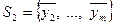 . Если все векторы
. Если все векторы 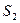 линейно выражаются через векторы
линейно выражаются через векторы  , то
, то
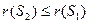
Доказательство:
Т.к. 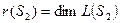 и
и 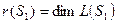 , то вышесказанное будет доказано, если докажем, что
, то вышесказанное будет доказано, если докажем, что 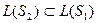 . Для любого
. Для любого 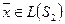 имеет разложение
имеет разложение 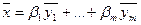 , но каждый вектор
, но каждый вектор  линейно выражается через
линейно выражается через 
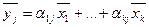 ,
, 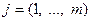
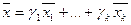 , (*)
, (*)
где  и т.д.
и т.д.
Из (*) 
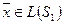 ,
, 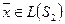 , т.е. есть включение
, т.е. есть включение 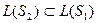 .
.
Элементарные преобразования системы векторов:
1) перестановка 2-х векторов;
2) умножение вектора на число, не равное 0;
3) добавление к одному вектору другого, умноженного на коэффициент.
Теорема.
При элементарных преобразованиях ранг сохраняется:
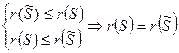 .
.
4.5 Базис и размерность линейного пространства.
Число n называется размерностью линейного пространства L, если:
1) в L существует система из n линейных векторов;
2) любая система из n+1 векторов в L – линейно зависима.
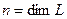
Замечание: В n -мерном пространстве L линейно зависима любая система из  вектора.
вектора.
Базисом n -мерного линейного пространства L называется всякая линейно независимая система в L, состоящая из n -векторов.
Базисы в линейных пространствах.
1)  ,
,  .
.
Базис в L – любая тройка некомпланарных векторов. Канонический базис:
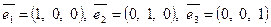 .
.
2) 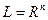 ,
, 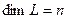 .
.
Базис в L образует, например, 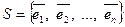 . Канонический базис:
. Канонический базис:
 .
.
3)  ,
, 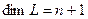 .
.
4) 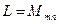 ,
, 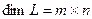 .
.
Канонический базис:
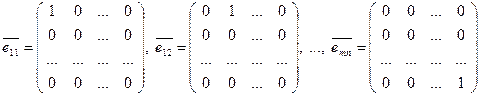 .
.
Библиографический список:
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1984.
2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1984.
3. Под редакцией Ефимова А.В., Демидовича Б.П. Сборник задач по математике для втузов. Ч.1. Линейная алгебра и математический анализ. – М.: Наука, 1986.
Последняя редакция:
12.2002 г.
[1] Существует также и другое обозначение определителя, которое может встретится далее:.
[2] А.Т. Вандермонд (1735 – 1796 гг.) – французский математик.
[3] Г. Крамер (1704 – 1752 гг.) – швейцарский математик.






