Расчет основных параметров для каждой

СТУПЕНИ РЕДУКТОРА

6.1 Предварительное значение межосевого расстояния

Для прямозубой передачи

Для косозубой передачи

В этих формулах:

коэффициенты 10 000 и 8 500, вычислены для стальных зубчатых колес при средних параметрах передач;

Т₂ – номинальный вращающий момент на валу колеса, Нм;

и – передаточное число;

К_н = 1,1…1,2 – коэффициент нагрузки при расчете на контактную выносливость.

К_На = 1,0…1,12 – коэффициент, учитывающий распределение нагрузки между зубьями в косозубых передачах;

коэффициент ширины зубчатых колес передачи, который при несимметричном расположении колес относительно опор рекомендуется выбирать в пределах 0,25…0,4. Если полученное значение то следует принять

[ ]_Н – допускаемое напряжение на контактную выносливость, которое выбирается в зависимости от выбранного материала зубчатых колес и способа термообработки, Мпа.

Полученные при расчете значения межосевых расстояний в мм следует округлять до ближайшего большего значения из ряда Ra40 по ГОСТ 6636-69. Для стандартных редукторов значения межосевых расстояний округляют до ближайших значений по табл. 6.1,

Таблица 6.1

Значения a_w, мм
1-й ряд	40 50 63 80 100 125 160 200 250 315 400 500 63 80 100 125 160 200 250 315 400 500
2-й ряд	71 90 112 140 180 224 280 335 450 450
1-й ряд	630 800 1000 800 1000
2-й ряд	560 710 900 1120 900 1120

Межосевое расстояние соосного редуктора определяется из расчета на контактную выносливость тихоходной ступени.

6.2 Рабочая ширина колеса b ₂ = a_w ;

ширина шестерни b ₁ = b ₂ +(2...4) мм

Полученные значения b ₁и b ₂в мм округляют до ближайших значений по ГОСТ 6636-69 (Приложение Г).

6.3 Ориентировочное значение модуля m, мм вычисляют по формуле

m = (0,01...0,02) a_w.

Полученное значение модуля округляют до ближайшего большего по табл. 6.2.

Таблица 6.2

Значения модуля т или т _n, мм

1-й ряд 1 1,5 2 2,5 3 4 5 6 7 8

2-й ряд 1,25 1,375 1,75 2,25 2,75 3,5 4,5 5,5 7 9 4,5 5.S 7 9

1-й ряд 10 12 16

2-й ряд 11 14 18

Применять модули меньше 1,5 мм для силовых передач не рекомендуется.

6.4 Суммарное число зубьев в угол наклона зуба

Для прямозубых зубчатых колес = 0;

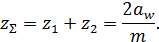
Значение z должно быть целым числом. При необходимости, для обеспечения этого условия, изменяют значения а и т.

Для косозубых зубчатых колес угол наклона зубьев рекомендуется принимать в пределах

β = (8…15)°

При предварительном расчете рекомендуется принять , для

шевронных зубчатых колес

Должно быть выдержано условие:

Если при выбранном угле значение получается дробным, его округляют до целого числа _z и определяют действительный угол .

Следует помнить, что в косозубых передачах при больших углах ( >20°) сильно возрастает осевая нагрузка на подшипники.

6.5 Число зубьев ведущего н ведомого колес

где 17 для прямозубых и = 1 7 cos³ длякосозубых и шевронных колес.

Значение также следует округлить до целого числа

6.6 Фактическое значение передаточного числа

Фактическое значение суммарного передаточного числа редуктора не должно отличаться от заданного более чем на 4%.

6.7 Определение основных параметров зубчатого зацепления

6.7.1 Диаметры делительных окружностей:

для прямозубых колес

для косозубых и шевронных колес

Точность определения значений диаметров делительных окружностей должна быть не менее 0,001 мм. После определения d ₁и d ₂проверяется равенство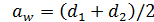

6.7.2 Диаметры окружностей вершин:

для прямозубых колес

для косозубых и шевронных колес

6.7.3 Диаметры окружностей впадин:

для прямозубых колес

для косозубых и шевронных колес

6.8 Силы, действующие в зацеплении

Для прямозубых колес (рис. 6.1) определяются окружная сила

и радиальная сила

Рисунок 6.1 – Силы, действующие в прямозубом зацеплении

Для косозубых и шевронных колес (рис. 6.2)определяется также осевая сила.

Окружная сила

Радиальная сила , где угол зацепления

Осевая сила

Рисунок 6.2 – Силы, действующие в непрямозубом зацеплении

ПРИМЕР РАСЧЕТА КОСОЗУВОЙ

ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ РЕДУКТОРА,