Используется для передачи вращения между перекрещивающимися осями.
Обычно угол скрещивания осей равен 90 ◦ (рис.11.5).
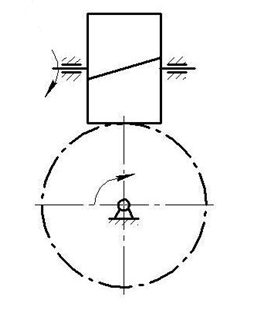
Рис.11.5
Рис.11.6
Состоит такая передача из двух винтовых (косозубых) эвольвентных колёс, которые обычно используются в косозубой передаче (лекция №10). Там же дана методика геометрического расчёта этих колёс.
Угол скрещивания осей в винтовой передаче (рис.11.6) равен:
+ 
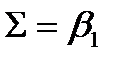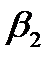. (если принять 
=- 
, то получаем вариант косозубой передачи с параллельными осями).
К достоинствам винтовой зубчатой передачи следует отнести:
а) простота и технологичность изготовления по методу огибания;
б) нечувствительность к погрешностям изготовления и монтажа:
в) плавность, бесшумность хода, используется как быстроходная.
Однако, передача имеет ограниченное применение ввиду малой нагрузочной способности. Причиной этого являются большие скорости скольжения в зацеплении и ярко выраженный точечный контакт зубьев.
Кинематический расчёт многоступенчатых передач.
Многоступенчатая передача с неподвижными осями зубчатых колёс состоит из ряда зубчатых пар, связанных в единую кинематическую цепь. Каждую зубчатую пару называют ступенью передачи. Задача кинематического расчёта многоступенчатой передачи состоит в том, чтобы определить передаточное отношение от ведущего вала к ведомому и направление вращения ведомого вала по заданному направлению вращения ведущего.
Пусть требуется выполнить кинематический расчёт четырёхступенчатой передачи (рис. 11.7). Ведущим валом, получающим движение от двигателя, служит вал с зубчатым колесом Z1. Зубчатое колесо Z7, связанное с последним ведомым валом, имеет в нашем примере внутренний зубчатый венец и образуется с колесом Z6 зубчатую пару внутреннего зацепления. Зубчатое колесо Z6 участвует в двух зубчатых парах. Известны числа зубьев зубчатых колёс.
Определяем передаточное отношение i17 = ω1/ω7 (где ω1 и ω7 - угловая скорость ведущего и ведомого валов), а также знак передаточного отношения.
Для того чтобы вывести формулу для определения передаточного отношения многоступенчатой передачи, его разбивают на сомножители по числу ступеней и заменяют отношения угловых скоростей зубчатых колёс на каждой ступени соответствующими обратными отношениями чисел зубьев. Для плоских передач можно учитывать знак передаточного отношения на каждой ступени.
Рис.11.7
Передаточному отношению тех ступеней, где применяется внешнее зацепление, приписывается знак “минус” (так как при этом изменяется направление вращения ведомого вала), в случае внутреннего зацепления – знак “плюс”.
Для схемы, предоставленной на рис.11.7, передаточное отношение разбивается на четыре сомножителя:
Отношения угловых скоростей заменяются обратными отношениями чисел зубьев с учётом знаков передаточного отношения:
Здесь Z1 - Z7 - числа зубьев зубчатых колёс. После подстановок получаем:
ֹ
Передаточное отношение рассматриваемой четырёхступенчатой передачи имеет знак «минус», следовательно, ведущий и ведомый валы вращаются в разные стороны. Зубчатое колесо Z6 не повлияло на числовое значение передаточное отношение, но изменило его знак. Такие зубчатые колёса называют паразитными колёсами. Их применяют для изменения направления вращения и для передачи движения между далеко отстоящими валами.
Лекция №12.
Планетарные механизмы.
Планетарные зубчатые механизмы отличаются от других зубчатых механизмов тем, что имеют зубчатые колёса с подвижными осями вращения. Планетарный механизм с одной степенью свободы называются планетарной передачей. Планетарный механизм с двумя степенями свободы называется дифференциальным механизмом.
При кинематическом расчёте планетарных механизмов применяется уравнение связи угловых скоростей (формула Виллиса), составленное для механизмов с двумя степенями свободы, частными случаями которых являются механизмы с одной степенью свободы (планетарные передачи). Вследствие этого кинематические схемы тех и других планетарных механизмов требуется рассматривать параллельно.
На рис. 12.1 и 12.2 представлены кинематические схемы двух планетарных механизмов, различающихся числом степеней свободы.
Зубчатые колёса а и в, имеющие общую неподвижную ось вращения, называются центральными зубчатыми колёсами, а зубчатое колесо S с подвижной осью вращения – сателлитом. Звено h, на котором размещены подшипники сателлита, именуется водилом. Ось вращения водила совпадает с общей осью центральных зубчатых колёс. Водило и центральные зубчатые колёса являются основными звеньями планетарного механизма.
Механизм, кинематическая схема которого представлена на рис.12.1, имеет две степени свободы. Два любых центральных звена этого механизма можно рассматривать как ведущие звенья. Например, ведущими звеньями могут быть колесо а и водило h, при этом колесо в становится ведомым звеном.
Рис.12.1 Рис.12.2
На рис.12.2 приведена кинематическая схема планетарной передачи. Она отличается от предыдущей схемы тем, что одно из центральных зубчатых колёс (колесо в) остановлено и закреплено на стойке, вследствие чего степеней свободы механизма уменьшилось на единицу. Этот механизм можно применять в качестве понижающей передачи (если передавать движение от колеса а к водилу h) или в качестве повышающей передачи (при передачи движения от водила на колесо а).
Из механизма с двумя степенями свободы можно получить вторую планетарную передачу, если остановить и закрепить на стойке зубчатое колесо а. При этом подвижными звеньями останутся колёсо в и водило h, каждое из которых можно рассматривать как ведущее звено.
Из любого пятизвенного планетарного механизма с двумя степенями свободы образуется две планетарные передачи путём поочередной остановки одного из центральных зубчатых колёс.
На рис. 12.3 представлены кинематические схемы пятизвенных планетарных механизмов с двумя степенями свободы, сателлиты которых имеют два зубчатых венца. Они отличаются друг от друга различными комбинациями способов зацепления центральных зубчатых колёс и зубчатых колёс сателлита (внешнее зацепление, внутреннее зацепление).
a – с двумя внешними зацеплениями;
б – с одним внешним и одним внутренним зацеплением;
в – с двумя внутренними зацеплениями.
Рис.12.3
На рис. 12.4 изображены кинематические схемы четырёхзвенных планетарных передач, полученных посредством остановки и закрепления центрального колеса в. Путём закрепления колеса а также можно образовать три планетарных передачи.
Рис. 12.4
На практике часто применяют планетарные механизмы, в которых зубчатые венцы S и t совмещены. В этом случае упрощается изготовление и сборка механизма. При совмещении зубчатых венцов сателлитов в планетарной передаче с одним внешним и одним внутренним зацеплением (рис. 12.4, б) получаем планетарную передачу, схему которой представлена на рис. 12.2.
В связи с выбором ведущего звена в планетарной передачи необходимо коснуться вопроса о потерях на трение в планетарных механизмах, которых выходит за рамки структурного и кинематического анализа, но имеет важное практическое значение.
При назначении ведущего звена для планетарной передачи с двумя внешними или двумя внутренними зацеплениями (рис.12.4, а, в) необходимо учитывать, что здесь в случае передачи движения от центрального колеса к водилу возможно резкое падение коэффициента полезного действие. При малой разности чисел зубьев зубчатых колёс S и t сателлита и в случае их совмещения происходит самоторможение, механизм не проворачивается. Ввиду этого ведущим звеном в упомянутых передачах служит, как правило, водило.
