Алгебра высказываний
Высказывание – это утверждение о котором можно сказать истинно оно или ложно. Высказывания будем обозначать малыми и большими буквами лат. алфавита. Предполагается, что имеется некоторый начальный набор высказываний, которые будем называть простейшими и обозн. малыми буквами. Если высказывание а истинно, то пишем а=1, а если ложно а=0. Из простейших выск. строятся сложные с помощью союзов: и, или, не, связки: если – то. Сложны выск. обозн. большими буквами(A,B,C…). Если сложное выск. А построенное из простых выск. а1,а2…аn то пишем А(а1,а2…аn) Опр.1 Отрицанием выск. а наз. выск. обозн. а‾, которое истинно если а ложно и ложно если а истинно. Опр2. Конъюнкцией 2 выск. а и b наз. выск. аb которое истинно когда оба. выск. истинны и ложно во всех остальных случаях. Опр3. Дизъюнкция двух 2 выск. а и b наз. выск. аVb которое истинно тогда и т.т., когдахотя бы одно из выск. истинно. Опр4. Импликацией 2 выск. а и b наз. выск a  b которое ложно тогда и т.т., когда а - истинно, а b – ложно. Т.е a
b которое ложно тогда и т.т., когда а - истинно, а b – ложно. Т.е a  b=0 только при а=1, b=0. Опр5. Эквивалентностьюдвух 2 выск. а и b наз. выск. а~b которое истинно тогда и т.т., когда а и b одновременно истинны или ложны. Опр6. А(а1,а2…аn) и B(а1,а2…аn), эти выск. наз. Равносильными если они принимают одинаковые истинные значения при соотв. Наборах истиностных значений входящих в них переменных, обозн. А≡B.
b=0 только при а=1, b=0. Опр5. Эквивалентностьюдвух 2 выск. а и b наз. выск. а~b которое истинно тогда и т.т., когда а и b одновременно истинны или ложны. Опр6. А(а1,а2…аn) и B(а1,а2…аn), эти выск. наз. Равносильными если они принимают одинаковые истинные значения при соотв. Наборах истиностных значений входящих в них переменных, обозн. А≡B.
Булевы функции
Пусть E={(0,1}. Опр. Пусть A и B - 2 непустых множества, декартовым произведением множеств A и B наз. новое мн-во A×B, которое состоит из всевозможных упорядоченных пар вида: A×B={(a,b) | a  A, b
A, b  B}. Из определения декартового произв. следует, что упор. Пара (а,b)=(c,d) тогда и только тогда, когда a=c, b=d, т.е соответствующие компоненты пар равны. Пусть А1,А2,….Аn не пустые множества, А1×А2...×Аn={(а1,а2…аn) | ai
B}. Из определения декартового произв. следует, что упор. Пара (а,b)=(c,d) тогда и только тогда, когда a=c, b=d, т.е соответствующие компоненты пар равны. Пусть А1,А2,….Аn не пустые множества, А1×А2...×Аn={(а1,а2…аn) | ai 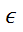 Ai, i=1..n}, которое по опр. состоит из всевозможных наборов длины n. Из опр. декартового произв. мн-в А1,А2,….Аn следует, что упорядоченный набор а1,а2…аn равен упор. набору b1,b2…bn т.и.т.т., когда аi=bi, т.е равны соотв. компоненты этих двух упорядоченных наборов. Если Ai =A, то А×А...×А= An и называют n-й декартовой степенью мн-ва A. Пусть n – нат. число, рассм. En={(а1,а2…аn) | ai
Ai, i=1..n}, которое по опр. состоит из всевозможных наборов длины n. Из опр. декартового произв. мн-в А1,А2,….Аn следует, что упорядоченный набор а1,а2…аn равен упор. набору b1,b2…bn т.и.т.т., когда аi=bi, т.е равны соотв. компоненты этих двух упорядоченных наборов. Если Ai =A, то А×А...×А= An и называют n-й декартовой степенью мн-ва A. Пусть n – нат. число, рассм. En={(а1,а2…аn) | ai 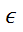 {0;1}, i=1..n} Опр. Отображение f мн-ва En в мн-во E наз. булевой функцией, а точнее булевой функцией от n переменных; Утв1. Число булевых ф-ций от n переменных равно 2 в степени 2n.
{0;1}, i=1..n} Опр. Отображение f мн-ва En в мн-во E наз. булевой функцией, а точнее булевой функцией от n переменных; Утв1. Число булевых ф-ций от n переменных равно 2 в степени 2n.
Элементарные булевы функции и их свойства
Основные булевы функции: 1)f1(x)=0,  x
x 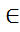 E – “константа 0” 2)f2(x)=1,
E – “константа 0” 2)f2(x)=1,  x
x 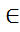 E – “константа 1” 3)f3(x)=x,
E – “константа 1” 3)f3(x)=x,  x
x 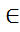 E – ”тождественная функция“ 4)f4(x)=x‾,
E – ”тождественная функция“ 4)f4(x)=x‾,  x
x 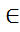 E – ”отрицание x“ 5)f5(x1,x2)=x1x2– ”конъюнкция x1 и x2“ 6)f6(x1,x2)=x1V x2– ”дизъюнкция x1 и x2“ 7)f7(x1,x2)=x1 → x2– ”x1 импликация x2“ 8)f8(x1,x2)=x1 ~ x2– ”x1 эквивалентность x2“ 9)f9(x1,x2)=x1 + x2– ”сложение по модулю 2 “ 10)f10(x1,x2)=x1 | x2– ”штрих Шефера (антиконъюнкция) “ 11)f11(x1,x2)=x1
E – ”отрицание x“ 5)f5(x1,x2)=x1x2– ”конъюнкция x1 и x2“ 6)f6(x1,x2)=x1V x2– ”дизъюнкция x1 и x2“ 7)f7(x1,x2)=x1 → x2– ”x1 импликация x2“ 8)f8(x1,x2)=x1 ~ x2– ”x1 эквивалентность x2“ 9)f9(x1,x2)=x1 + x2– ”сложение по модулю 2 “ 10)f10(x1,x2)=x1 | x2– ”штрих Шефера (антиконъюнкция) “ 11)f11(x1,x2)=x1 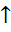 x2– ”стрелка Пирса (антидизъюнкция) “ Основные эквивалентности формул: Пусть
x2– ”стрелка Пирса (антидизъюнкция) “ Основные эквивалентности формул: Пусть 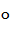 означает
означает  ,V,+ 1) (x1
,V,+ 1) (x1 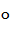 x2 )
x2 ) 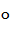 x3=x1
x3=x1 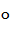 (x2
(x2 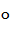 x3) – ассоциативность операции
x3) – ассоциативность операции 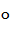 2) x1
2) x1 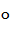 x2= x2
x2= x2 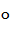 x1 – коммутативность операции
x1 – коммутативность операции 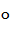 3)
3) 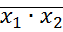 =
= 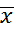 1
1 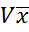 2 ;
2 ; 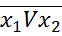 =
= 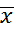 1
1  2 – законы де Моргана. 4)
2 – законы де Моргана. 4) 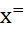 =х – двойное отрицание, x1 →x2=
=х – двойное отрицание, x1 →x2= 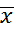 1 V x2 5) (x1V x2)
1 V x2 5) (x1V x2)  x3=x1
x3=x1  x3V x2
x3V x2  x3 ; (x1
x3 ; (x1  x2)
x2) 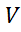 x3=(x1
x3=(x1 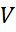 x3)
x3)  (x2 V x3) – дистрибутивности связывающие конъюнкцию и дизъюнкци 6)x1V(x1
(x2 V x3) – дистрибутивности связывающие конъюнкцию и дизъюнкци 6)x1V(x1  x2)=x1; x1
x2)=x1; x1  (x1
(x1 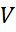 x2)=x1 – законы поглощения. 7) xVx=x; x
x2)=x1 – законы поглощения. 7) xVx=x; x  x=x – законы идемпатентности 8) x
x=x – законы идемпатентности 8) x  =0 – закон противоречия; 9) x V
=0 – закон противоречия; 9) x V 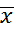 =1 – закон исключения третьего.
=1 – закон исключения третьего.






