Список использованных источников. Исследование полноты системы булевых функций.

ЛАБОРАТОРНАЯ РАБОТА 2.

 

Исследование полноты системы булевых функций.

 

Цель работы: Изучить методику исследования полноты системы булевых функций по теореме Поста.

 

Порядок выполнения работы.

1. Изучить теоретические сведения.
2. Получить задание у преподавателя.
3. Исследовать полноту системы булевых функций по теореме Поста.
4. Сделать выводы по результатам исследований.
5. Оформить отчет.

Требования к отчету.

1. Цель работы.
2. Постановка задачи.
3. Результаты исследования по пяти классам булевых функций.
4. Таблица Поста.
5. Выводы.

 

Теоретические сведения.

Основные понятия

Пусть K — некоторое множество функций алгебры логики. Замыканием [ K ] множества K называется совокупность всех функций из Р₂, являющихся суперпозициями функций из множества K. Множество K называется замкнутым классом, если [ K ]= K. Пусть K – замкнутый класс в Р ₂. Подмножество P из K называется функционально полной системой в K, если [P] = K.

Множество K’, содержащееся в замкнутом классе K (в т.ч. K=P ₂), называется предполным классом в K, если оно не является полной системой в K, но для всякой функции выполняется равенство

Самодвойственные функции

Функция 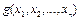называется двойственной к , если = . Двойственная функция обозначается .

Функция называется самодвойственной, если = 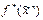. Класс самодвойственных функций обозначается S.

Линейные функции

Функция называется линейной, если она представима в виде

Множество всех линейных функций обозначается L.

Функции, сохраняющие константу

Говорят, что функция сохраняет константу 0 (константу 1), если f (0,0,...,0)=0 (cоответственно, f (1,1,...,1)=1). Множества функций, сохраняющих константу 0 или 1, обозначаются соответственно T ₀ и T ₁.

Монотонные функции

Булева функция называется монотонной, если для любых двух наборов из , таких, что имеет место неравенство

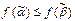. В противном случае функция называется немонотонной.

Вершина куба называется нижней единицей (верхним нулем) монотонной функции , если =1 ( =0) и для всякой вершины из вытекает, что =0 (соответственно из вытекает =1). Множество монотонных функций обозначается M.

Каждое из множеств T ₀, T ₁, S, L, M является замкнутым и предполным классом в P ₂.

Теорема. Система K полна в Р ₂ тогда и только тогда, когда она целиком не содержится ни в одном из классов T ₀, T ₁, S, L, M.

ЗАДАНИЕ 1.

1. Является ли множество K замкнутым классом:

1) K ={0,1}; 2) K = { }; 3) K = { 1, };

4) K = {0, }.

2. Сведением к заведомо полным системам в P₂ , доказать полноту системы K:

1) K = { }; 2) K = { };

3) K = { }; 4) K = { }.

3. Доказать, что всякий предполный класс в Р ₂ является замкнутым классом.

4. Является ли функция g двойственной к f, если

1) f = x y, g = x ~ y; 2) f = x y, g = y x.

5. Является ли функция самодвойственной:

6. Подсчитать число самодвойственных функций, существенно зависящих от переменных

7. Доказать, что если 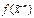— самодвойственная функция, то .

8. Разлагая функцию f в полином Жегалкина, выяснить, является ли она линейной:

9. Доказать, что для любой ф.а.л. существует единственное разложение в полином Жегалкина.

10. Доказать, что если f — линейная функция и f  const, то

11. Найти число линейных самодвойственных функций.

12. Доказать, что .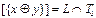

13. Доказать, что если на любых двух соседних наборах принимает противоположные значения,

то она линейная.

14. Показать, что всякая монотонная функция содержится не менее, чем в двух классах из { }.

15. Функция f не принадлежит множеству { } и принимает в точности одно значение, равное нулю.

Доказать, что она либо является шефферовской, либо существенно зависит лишь от одной переменной.

16. Какие из перечисленных ниже функций являются монотонными:

17. Подсчитать число функций в каждом из следующих множеств:

18. Показать, что если 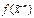немонотонна, то существуют такие два вектора и из , различающиеся

ровно в одной координате, что , но .

19. Показать, что в Р ₂ не существует предполных классов, отличных от классов T ₀, T ₁, S, L, M.

20. Используя критерий полноты, выяснить, полна ли система Р:

1) P = { 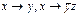}; 2) P = { };

3) P = {0, 1, }.

21. Доказать, что любую функцию из Р ₂ можно представить через логические связки: конъюнкцию,

дизъюнкцию и отрицание.

22. Пусть и 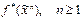удовлетворяет условию = 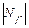. Доказать, что если , то .

23. Из самодвойственной функции f с помощью подстановки на места переменных получить константу

24. Можно ли из функции f =(10110010) с помощью операции суперпозиции получить функцию g =(1000)?

25. Показать, что , где – совокупность всех функций, двойственных к линейным функциям.

 

ЗАДАНИЕ 2.

Список использованных источников

1 Показеев, В.В. Элементы дискретной математики: Курс лекций / В.В. Показеев, В.И. Матяш, Г.В. Черкесова. – М.: МГТУ МАМИ, 2003. – 239 с.

2. Кирсанов, М.М. Дискретная математика: Основные тезисы / М.М. Кирсанов, В.В. Показеев. – М.: МГТУ МАМИ, 2003. – 26 с.

3. Москинова, Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях: Учебное пособие / Г.И. Москинова. – М.: Логос, 2003. – 240 с.