Т. к. f (0,0,1) < f (0,1,0) и f (0,1,0) > f (0,1,1), значит, данная функция не относится к классу монотонных функций.
Т. к., например f (0,0,0) = f(1,1,1), то данная функция не относится к классу самодвойственных функций.
Т. к. не выполняется условие f (0,1,1) = f (1,0,1) = f (1,1,0) / значения соответственно равны 0,1,1/, то данная функция не относится к классу симметрических функций.
Проверим принадлежность функции к классу линейных функций.
Для этого запишем ее в таком виде:
f1(x1,x2,x3) = C0 Å C1&X1 Å C2&X2 Å C3&X3.
Найдем коэффициенты Ci:
f (0,0,0) = 1 / из таблицы истинности /
С0 Å С1&0 Å C2&0 ÅC3&0 = 1, т.о., С0 = 1.
f (1,0,0)=0 / из таблицы истинности /
0 Å C1 &1 Å C 2&0 Å C 3&0 = 0, т.о., С 1 = 1.
f (0,1,0) = 1/ из таблицы истинности /
0 Å C1 &0 Å C 2&1 Å C 3&0 = 1, т.о., С 2 = 0.
f (0,0,1) = 0 / из таблицы истинности /
0 Å C 1&0 Å C 2&0 Å C 3&1 = 0,т.о., С 3 = 0.
Тогда f1(x1,x2,x3) = 1.
Сравним значения функций f и f 1 по таблице истинности:
| № х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1 | f(x1,x2,x3) 1 | f1(x1,x2,x3) |
Т. к. значения функций различны для одинаковых наборов, то данная
функция не относится к классу линейных функций.
Ответ: данная функция относится к классу констант «1»
Задание 5. Необходимо для данной функции найти её ДСНФ, КСНФ, ЭСНФ, ИСНФ, принимающей значения 1 на следующих наборах: 0, 1, 2, 3,6,12
Решение:
Составим таблицу истинности
| № | x1 x2 x3 x4 | f(x1 x2 x3 x4) |
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
Для получения ДСНФ, ПСНФ используем термы для 1 значений функции:
ДСНФ: f(x1,x2,x3,х4 ) =
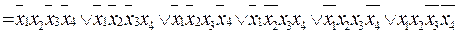
ПСНФ: f(x1,x2,x3,х4)=
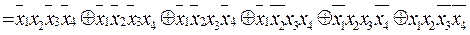
Для получения КСНФ, ЭСНФ используем термы для 0 значений функции:
КСНФ:
f(x1,x2,x3,х4)= 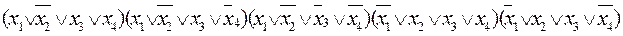
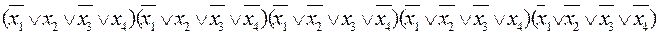
ЭСНФ:
f(x1,x2,x3,х4)=
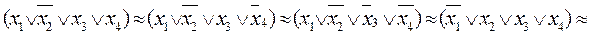
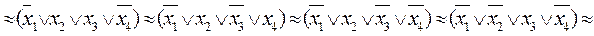
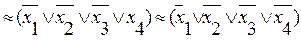
ИСНФ:
1) Для получения первой формы ИСНФ 1 используем термы для 1 значений функции:
f(x1,x2,x3,х4) =
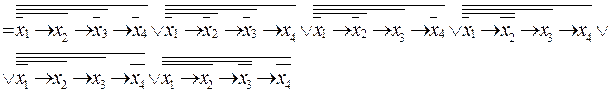
2) Для получения второй формы ИСНФ 0 используем термы для 0 значений функций:
f(x1,x2,x3,х4)=
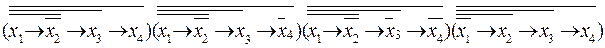
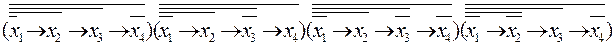
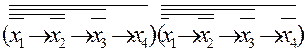
Задание 6. Используя метод Квайна, необходимо найти МДНФ функции, принимающей значения 1 на наборах: 2, 3, 6, 7, 11.
Решение:
Составим таблицу истинности
| № | x1 x2 x3 x4 | f(x1 x2 x3 x4) |
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
Выпишем термы для 1 значений функции и склеим все возможные:
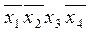 (1) (1)
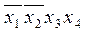 (1) (1)
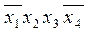 (2) (2)
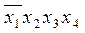 (2) (2)
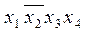
| 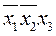
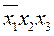
| 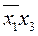
|
Составим таблицу и найдем минимальное покрытие:
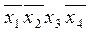
| 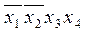
| 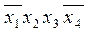
| 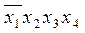
| 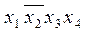
| |
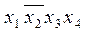
| + | ||||
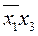
| + | + | + | + |
В данном случае
f1(x1,x2,x3,x4) = 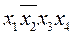 ˅
˅ 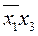
Задание 7. Используя метод Квайна – Мак-Класки, необходимо найти МНДФ функции, принимающей значения 1 на наборах: 6, 7, 8, 10, 11, 13.
Решение:
Составим таблицу истинности
| № | x1 x2 x3 x4 | f(x1 x2 x3 x4) |
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
Составим группы по количеству 1 и выполним необходимые преобразования:
1)
0 группа -
I группа - 1000
II группа – 0110, 1010
III группа - 0111, 1011, 1101
IV группа -
2)
0 группа -
I группа - 10_0
II группа – 011_, 101_
III группа -
Составим таблицу и найдем минимальное покрытие:
| 10_0 | 011_ | 101_ | ||
| + | ||||
| + | ||||
| + | ||||
| + | ||||
| + | ||||
| + |
f1(x1,x2,x3,x4) = 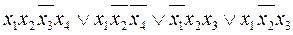
Задача 8. Используя метод диаграмм Вейча, необходимо найти МДНФ функции, принимающей значение 1 на наборах: 2, 3, 4, 5, 10, 12, 13, 15.
Решение:
Составим таблицу истинности
| № | x1 x2 x3 x4 | f(x1 x2 x3 x4) |
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
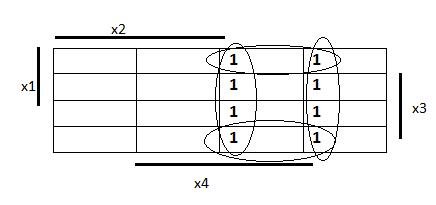
f1(x1,x2,x3,x4) = 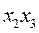 ˅
˅ 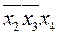 ˅
˅ 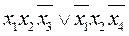
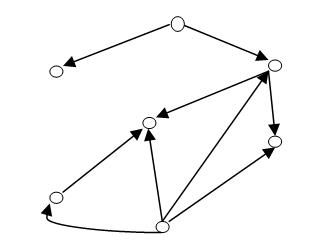
Задание 9. Задать граф следующим образом: перечислением, матрицами смежности и инцидентности.
Введем обозначения вершин и дуг у графа
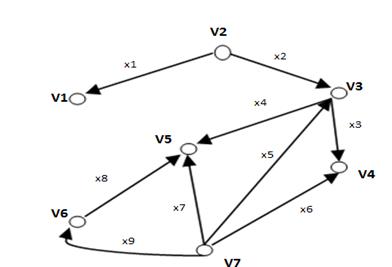
Способ перечисления:
Множество вершин: V = {v1, v2, v3, v4, v5, v6,v7}
Множество дуг: Х = { x1, x2, x3, x4, x5, x6,x7, x8, x9}
Матрица смежности графа 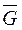
A(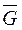 )7×7 = aij =
)7×7 = aij = 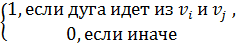

Матрица инцидентности графа 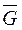 :
:
B(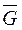 )6×95 = bij =
)6×95 = bij = 
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | |
| v1 | |||||||||
| v2 | -1 | -1 | |||||||
| v3 | -1 | -1 | |||||||
| v4 | |||||||||
| v5 | |||||||||
| v6 | -1 | ||||||||
| v7 | -1 | -1 | -1 | -1 |
Задание 10. Определить следующие основные характеристики графа:
– Число рёбер и дуг;
– Число вершин;
– Коэффициент связности графа;
– Степень всех вершин;
– Цикломатическое число графа.
Решение:
Число ребер – 0
Число дуг – 9
Число вершин – 7
Коэффициент связности графа – 1
Степень всех вершин
| v1 | v2 | v3 | v4 | v5 | v6 | v7 | |
| Полустепень исхода | |||||||
| Полустепень захода | |||||||
| Степень |
Цикломатическое число μ(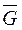 ) ориентированного графа определяется по формуле:
) ориентированного графа определяется по формуле:
μ(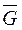 ) = |E(
) = |E(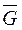 )| - |V(
)| - |V(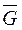 )| + k, где
)| + k, где
|E(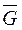 )| - число ребер графа.
)| - число ребер графа.
|V(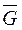 )| - число вершин графа.
)| - число вершин графа.
k – число компонент связности.
То есть, μ(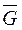 ) = |E(
) = |E(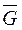 )| - |V(
)| - |V(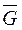 )| + k = 9 – 7 + 1 = 3
)| + k = 9 – 7 + 1 = 3
Задание 11. Определить, является ли данный граф:
– Планарным или плоским (обосновать ответ и выполнить обратное преобразование);
– Двудольным графом (обосновать ответ и если необходимо, то достроить до двудольного);
– Деревом (обосновать ответ, в случае циклического графа, привести один из вариантов основного дерева);
– Псевдографом или мультиграфом, или простым графом (обосновать ответ и выполнить необходимые преобразования).
Решение:
Данный граф является плоским, поскольку все его связи пересекаются только в вершинах.
Преобразуем данный граф в планарный.
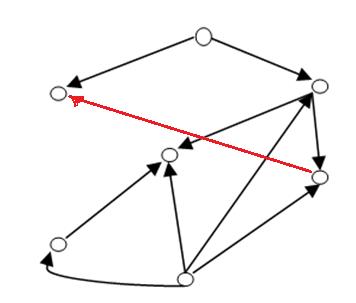
Двудольный граф – граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.
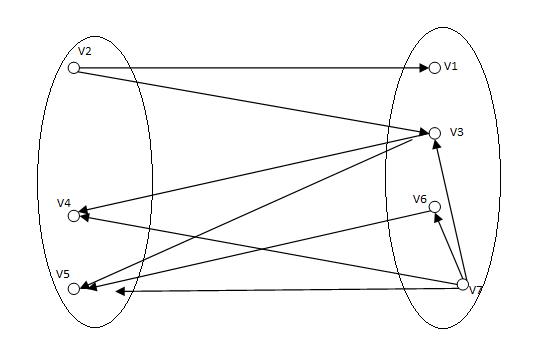
У данного графа такое не выполняется, следовательно достроим до двудольного
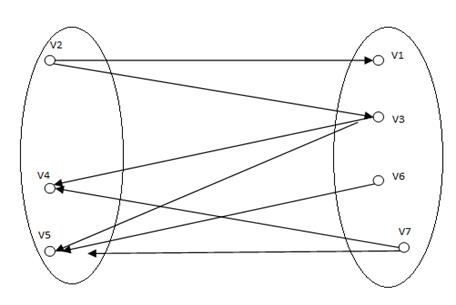
Данный граф не является деревом, поскольку он содержит циклы. Приведем пример остова данного графа.
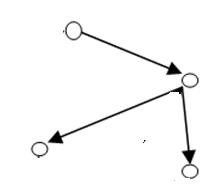
Данный граф является простым.
Граф, в котором могут быть и кратные ребра и петли называется псевдографом. Достроим граф до псевдографа.
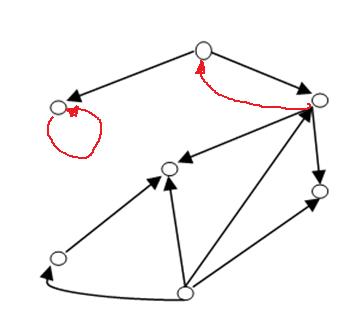
Псевдограф без петель является мультиграфом. Достроим граф до мультиграфа.
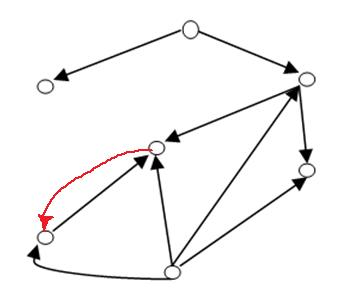
Задание 12. Определить метрические характеристики графа: диаметр, радиус, эксцентриситет каждой вершины, центральные вершины.
Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами dij которой будут расстояния между вершинами vi и vj. Для этого воспользуемся графическим представлением графа.
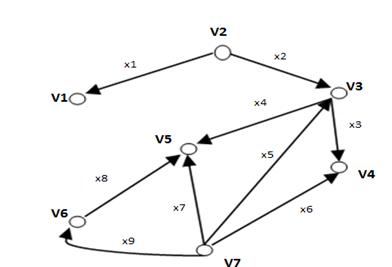
D(G) = 
С помощью полученной матрицы для каждой вершины графа G определим наибольшее расстояние из выражения: r(vj) = max d(vi,vj) для i, j = 1, 2, …,5. В результате получаем эксцентриситеты вершин: r(v1) = 0, r(v2) =2, r(v3) =1, r(v4) = 0, r(v5) =0, r(v6) = 1, r(v7) = 1.
Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 0 и D(G) = 2, центром являются вершины v1, v4, v5.
Задание 13. Написать программу, которая находит элементы множества
D = АU(A∩B)
Решение:
Program d;
uses crt;
const a=[1,2,3,5,7,8,10]
b=[1,2,3,5];
var r:set of byte;
i: byte;
begin
clrscr;
writeln;
r:=a-b;
for i:=1 to 255 do
var r:set of byte;
i: byte;
begin
clrscr;
writeln;
d:=a+r;
for i:=1 to 255 do
if i in r then write(i,’ ‘);
readln;
end.
Задание 14. Задать бинарное отношение, которое удовлетворяет следующим свойствам: P Í А и Р = {(x, y): x + y = 0, где x, y Î А – множество, вводимое пользователем}. В множестве А не должно быть повторяющихся элементов, оно должно быть упорядоченно по возрастанию и содержать не менее 10 элементов.
Написать программу, проверяющую какими свойствами обладает данное бинарное отношение.
Решение:
A = { -3; -2; -1; 1; 2; 3; 4; 5; 6; 7}
P = (-3;3), (-2;2), (-1;1),(1;-1),(2;-2),(3;-3)
Проверим все свойства отношения:
1) Рефлексивность 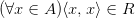 - это ложное высказывание
- это ложное высказывание
2) Антирефлексивность
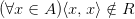 - это истинное высказывание
- это истинное высказывание
При х = 1 пара (-1;1) принадлежит Р.
3) Корефлексивность
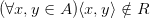 - это ложное высказывание
- это ложное высказывание
При х = -1 y = 1 пара (-1;1) принадлежит Р
4)Симметричность
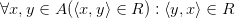 - это ложное высказывание
- это ложное высказывание
5) Антисимметричность
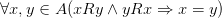 - это ложное высказывание
- это ложное высказывание
6) Асимметричность
Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения и отношение не является антирефлексивным, отношение не является асимметричным.
7) Транзитивность
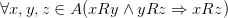 - это ложное высказывание
- это ложное высказывание
При х = -1 y = 1 z = 7 пара (-1;1) принадлежит Р, а пара (1;7) не принадлежит Р
8) Связность
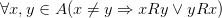 - это ложное высказывание
- это ложное высказывание
При х = 1 y = 3 1≠3 пара (1;3) не принадлежит Р и пара (3;1) не принадлежит Р
Заданное бинарное отношение обладает свойством антирефлексивности
Программа С++
| #include <iostream> #include <conio.h> #include <stdio.h> #include <fstream> #include <locale.h> #include <math.h> using namespace std; //перегрузка функции void Display(int A[],int k, int m[4][4]); void Display(int A[],int k, int** m); // сортировка void SortMas(int a[], long N){ long i = 0, k = N; int temp; bool flag = 0; while (flag!= true){ flag = true; for (i=0; i < k-1; i++){ if (a[i] > a[i+1]){ temp = a[i]; a[i] = a[i+1]; a[i+1] = temp; flag = false; } } } } // cоздание множества void MakeSet(int m[], int k, int n){ int i, j; srand(time(0)); for (i = 0; i < k; i++){ m[i] = rand()%n+1; int j = 0; while (j < i){ if (m[i] == m[j]){ m[i] = rand()%n+1; j=-1; } j++; } } } //Вывoд на экран void Display(int A[],int k, int** m){ //output of set cout<<"\n\n"; cout<<" |"; for (int i = 0; i < k; i++){ cout.width(3); cout<<A[i]<<" |"; } //print line cout<<"\n"; cout<<" "; for(int i = 0; i < k+1; i++){ cout<<"-----"; } cout<<"\n"; //print array for (int i = 0; i < k; i++){ cout<<" "; cout.width(4); cout<<A[i]<<" |"; for (int j = 0; j < k; j++){ cout.width(3); cout<<m[i][j]<<" |";; } if(i < k-1){ cout<<"\n"; cout<<" "; for(int i = 0; i < k+1; i++) { cout<<"-----"; } } cout<<"\n"; } //print line cout<<" "; for(int i = 0; i < k+1; i++){ cout<<"-----"; } } void Display(int A[],int k, int m[4][4]){ //output of set cout<<"\n\n"; cout<<" |"; for (int i = 0; i < k; i++){ cout.width(3); cout<<A[i]<<" |"; } //print line cout<<"\n"; cout<<" "; for(int i = 0; i < k+1; i++){ cout<<"-----"; } cout<<"\n"; //print array for (int i = 0; i < k; i++){ cout<<" "; cout.width(4); cout<<A[i]<<" |"; for (int j = 0; j < k; j++){ cout.width(3); cout<<m[i][j]<<" |";; } if(i < k-1){ cout<<"\n"; cout<<" "; for(int i = 0; i < k+1; i++) { cout<<"-----"; } } cout<<"\n"; } //print line cout<<" "; for(int i = 0; i < k+1; i++){ cout<<"-----"; } } // проверка на рефлексивность int ref (int m[4][4], int k){ int q; for (int i = 0; i<k; i++){ if (m[i][i]==0){ //если на диагонали есть 0 - нет q=0; break; } else q=1; //иначе - рефлексивно } return q; } //проверка на антирефлексивность int antiref (int m[4][4], int k){ int q; for (int i = 0; i<k; i++){ if (m[i][i]==1){ //если на диагонали есть 0 - нет q=0; break; } else q=1; // иначе антирефлексивно } return q; } //проверка на симметричность int sym (int m[4][4], int k){ int q=0; for (int i = 0; i<k; i++){ for (int j = 0; j<k; j++){ if (m[i][j]==m[j][i] && m[i][j]==1 && m[j][i]==1 && i!= j) q++; } } if (q>0) return 1; //возвращает 1 если есть симметрия и else return 0; } //проверка антисимметричности int antisym (int m[4][4], int k){ int q; for (int i = 0; i<k; i++){ for (int j = 0; j<k; j++){ if ((m[i][j]==m[j][i]==1 && i==j) || (m[i][j]==0 && i!=j) || (m[i][j]!=m[j][i])) q=1; //если отношение выполняется как для а и в так и обратно то только на диагонали, антитогда симметрично //иначе нет else { q=0; break; } } if (q==0) break; } return q; } //проверка ТРАНЗИТИВНОСТИ //РЕАЛИЗОВАНО С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМА УОРШЕЛЛА - ФЛОЙДА int trans (int a[4][4], int k){ int mat[4][4]; int q=0; //копируем матрицу истинности в mat[4][4] for (int i = 0; i<4; i++) for (int j = 0; j<4; j++) mat[i][j]=a[i][j]; //алгоритм Уоршелла - Флойда. Выполняет транзитивное замыкание // отношения заданного матрицей истинности mat[4][4] for (int l = 0; l<k; l++) for (int i = 0; i<k; i++) for (int j = 0; j<k; j++) mat[i][j] = (mat[i][j] || (mat[i][l] && mat[l][j])); //Выполним сравнение mat[4][4] и а[4][4] //если они равны, отношение а[4][4] транзитивно, иначе - нет. for (int i = 0; i<4; i++) for (int j = 0; j<4; j++){ if (mat[i][j] == a[i][j]) q=1; else { q=0; return q;} } return 1; } int main (){ srand(time(0)); int key; int i; int Na; do{ system("cls"); cout<<"\n"; cout<<" Please, input size set A --> "; cin>>Na; }while (Na<1 || Na>10); int *A = new int[Na];//выделение памяти для множества А int **M = new int *[Na]; //выделение памяти для матрицы истинности for (int i = 0; i<Na; i++){ M[i] = new int [Na]; } int M2[4][4] = { 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 }; int A2[4] = {1, 2, 3, 4}; MakeSet(A,Na,15);// создание множества А SortMas(A,Na); // сортировка множества А do { system("cls"); cout<<"\n\n\n"; cout<<" MENU: \n"; cout<<" 1) Output the matrix of truth for the relationship antisymmetry... \n"; cout<<" 2) Output the matrix of truth for the relationship transitivity... \n"; cout<<" 3) Check the properties of relations... \n"; cout<<" If you want to EXIT input 0\n"; cout<<" Please make your choice. --> "; cin>>key; // putchar (key); switch (key){ case 1:{ system("cls"); cout<<"\n DEMO of antisymmetry relation: R = ((b >= a) && (a+b)^2 % 3!= 0)? 1: 0"; for (int i = 0; i<Na; i++){ for (int j = 0; j<Na; j++){ M[i][j] = ((A[j] >= A[i]) && (A[i]+A[j])*(A[i]+A[j]) % 3!= 0)? 1:0; } } Display(A,Na,M); cout<<"\n\n Press any key!> "; getch(); break; } case 2:{ system("cls"); cout<<"\n."; cout<<"\n DEMO of transitivity relation: R = A:B? 1: 0"; for (int i = 0; i<Na; i++){ for (int j = 0; j<Na; j++){ M[i][j] = (A[i] % A[j] == 0)? 1:0; } } Display(A,Na,M); cout<<"\n\n Press any key!> "; getch(); break; } case 3:{ system("cls"); cout<<"\n Check the properties of relation R(A)={{1,1},{1,2},{2,1},{2,2},{3,3},{4,4}}:"; Display(A2,4,M2); cout<<"\n This relation is: "; if (ref(M2,4)) cout<<"\n -reflexive"; if (antiref(M2,4)) cout<<"\n -antireflexive"; if ((ref(M2,4) + antiref(M2,4))==0) cout<<"\n -not refleksive not antirefleksive"; if (sym(M2,4)) cout<<"\n -symmetric"; if (antisym(M2,4)) cout<<"\n -antisymmetric"; if (trans(M2,4)) cout<<"\n -transitive"; else cout<<"\n -not transitive"; cout<<"\n\n Press any key!> "; getch(); break; } } } while (key!= 0); delete []A; for (int i = 0; i<Na; i++){ delete[] M[i]; } delete[] M; return 0; } |






