Размеры на чертежах указываются размерными числами и размерными линиями, ограниченными стрелками или засечками. Основные требования по простановке размеров на чертежах показаны на рисунке 8.
Ознакомившись с требованиями к простановке размеров, студенты выполняют графическую работу, варианты заданий к которой представлены в приложении 4.






Рис. 8
Графическая работа №3
Наименование «Простановка размеров».
Формат А3.
Содержание работы: в каждом варианте дано по два примера, которые позволяют проработать основные принципы нанесения размеров на симметричную и несимметричную детали. Чертежи заданий выполнены на клетчатой бумаге. Для определения размеров детали считать сторону клетки равной 5 мм. Размеры проставлять с точностью до 1 мм. Перед выполнением задания внимательно изучить пример решения данного задания, представленный на рисунке 9.

Рис. 9
1.5 Геометрические построения
Геометрические построения широко применяются при решении различных задач с применением чертежных инструментов. Умея комбинировать в работе угольник и линейку, два угольника, циркуль и линейку можно выполнять построения параллельных прямых, опускать и восстанавливать перпендикуляры, делить углы и окружности на заданное количество равных частей, а так же строить углы определенной величины. Примеры некоторых построений приведены на рисунке 10, 11.


а) б)


в) г)
Рис. 10
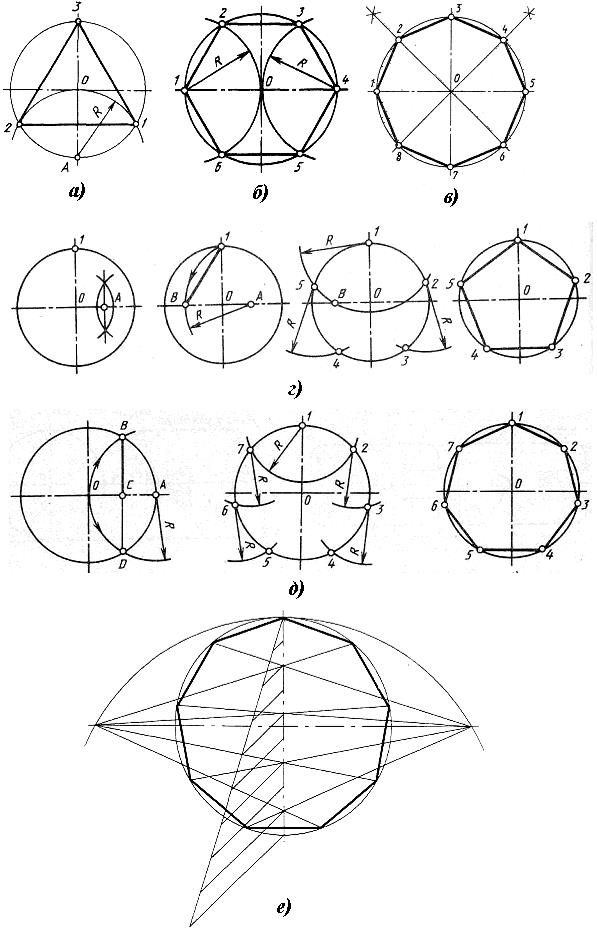
Рис. 11
Умение выполнять геометрические построения предполагает знание правил выполнения сопряжений – плавных переходов дуги к дуге, прямой к дуге, необходимых для вычерчивания контуров деталей. Выполнение таких построений показаны на рисунке 12.


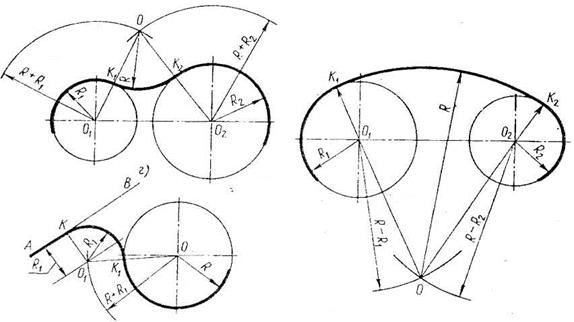
Рис. 12
Для приобретения навыков указанных построений рекомендуется выполнить их в рабочей тетради.
Графическая работа №4
Наименование «Контур детали»
Формат А3.
Содержание работы: В соответствии с вариантом (приложения 5а, 5б) выполнить чертежи деталей, проставить необходимые размеры. Вспомогательные линии построения сохранить.
Методические указания
Для того, чтобы вычертить контур, необходимо прочитать чертеж, т. е. определить общий контур детали, типы образующих его сопряжений.
Вычерчивание симметричных контуров начинать с осей симметрии.
Работу выполнять твердым карандашом.
Для обводки использовать карандаш «М», «ТМ» и лекало.
Ознакомиться с примером выполнения данной графической работы (рис.13)
|

Рис.13
Раздел 2 . Основы начертательной геометрии и проекционное черчение
2.1 Методы проецирования. Ортогональные проекции точки, прямой, плоскости, тела.
Начертательная геометрия изучает способы построения изображений пространственных фигур на плоскости и решения пространственной задачи на чертеже. Проекционное черчение рассматривает практические вопросы построения чертежей.
Все разделы начертательной геометрии пользуются одним методом – методом проецирования, поэтому чертежи называются проекционными изображениями.
Метод проецирования заключается в том, что любая из множества точек пространства может быть спроецирована с помощью проецирующих лучей на любую поверхность.
Существуют несколько методов проецирования. Центральное проецирование – получение проекций с помощью проецирующих лучей, проходящих через точку S, которую называют центром проецированию (рис. 14,а). Чертежи, применяемые во всех отраслях промышленности и строительства, выполняются методом ортогонального (прямоугольного) проецирования, являющегося частным случаем метода параллельного проецирования, когда проецирующие лучи параллельны между собой и перпендикулярны к плоскости проекции
(рис. 14,б).

а)

б)
Рис. 14
Этот метод позволяет спроецировать любую точку пространства на плоскости проекций: горизонтальную П1; фронтальную П2; профильнуюП3, обеспечивая при этом обратимость чертежа. Точки А1, А2,А3 - проекции точки А на соответствующие плоскости проекций.
Положение точки в пространстве определяют координаты: по оси Х – абсцисса, по оси У – ордината, по оси Z - аппликата (рис.15,а).
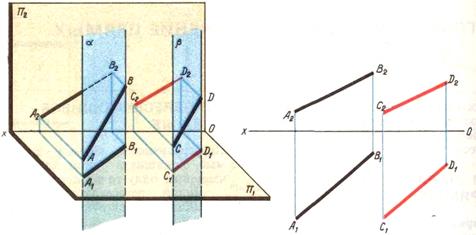
Преобразование пространственного изображения проецирования точки на плоскости П1, П2 и П3 в комплексный чертёж показано на рисунке 15,б.
Если даны две проекции точки, то можно построить третью, т. к. все проекции связаны между собой линиями проекционной связи.

Рис. 15
Проецирование отрезка прямой сводится к проецированию крайних точек отрезка (рис. 16).

Рис. 16
Ортогональное направление проецирующих лучей обусловливает ряд инвариантных (т.е. неразрушимых в процессе проецирования) свойств, основные из которых приведены ниже.
Проекция точки – всегда точка.
Проекция прямой – всегда прямая.
Точка принадлежит прямой тогда, когда ее проекции принадлежат соответствующим проекциям прямой.
Прямая задана, если заданы две ее проекции.
Располагаться в пространстве прямые могут следующим образом: параллельно друг другу (рис.17,а), пересекаясь (рис.17,б), скрещиваясь (рис.17,в).
По отношению к плоскостям проекций прямые могут быть проецирующими (перпендикулярными Пi), прямыми уровней (параллельными Пi), принадлежать одной из плоскостей проекций – это прямые частногоположения. В противном случае прямая является прямой общего положения.
а)

б)

в)
Рис. 17
Освоив методы ортогонального проецирования точек и прямых, можно выполнять проецирование плоскостей, задавая их одним из способов, показанных на рисунке 18:
18, а – тремя точками;
18, б – точкой и прямой;
18, в – двумя параллельными прямыми;
18, г – двумя пересекающимися прямыми.

а) б)

в) г)
Рис. 18
В зависимости от расположения плоскостей по отношению к плоскостям проекций они могут быть плоскостями общего или частного положения.
Необходимо помнить:
· если две точки прямой принадлежат плоскости, то вся прямая принадлежит плоскости;
· если точка лежит в плоскости, она должна принадлежать прямой, лежащей в этой плоскости;
· плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости;
· если прямая не параллельна плоскости, она пересекает ее;
· пересекаясь, две плоскости образуют прямую.
Изучив правила проецирования точек, прямых и плоскостей, можно выполнять чертежи геометрических тел, элементами которых они являются. Геометрические тела можно разделить на две группы: многогранники (тела, ограниченные плоскими многоугольниками) и тела вращения.
Примеры многогранников: призма, пирамида.
Примеры тел вращения: цилиндр, конус.
Для приобретения навыков построения ортогональных чертежей геометрических тел, а также в целях подготовки к выполнению графической работы, предлагается в рабочей тетради выполнить упражнение в соответствии с заданием, указанным в приложении 6. Формат для выполнения подобрать самостоятельно, учитывая обязательное расположение формата А4 по вертикали. Упражнение выполняется фронтально (всеми студентами вне зависимости от варианта графических работ).
Перед выполнением аксонометрических проекций заданных геометрических тел необходимо изучить п.2.2 данного пособия.
2.2 Аксонометрические проекции применяются для наглядного изображения предметов. Выполняются они в соответствии с ГОСТ 2.317-69. Аксонометрические проекции отличаются большой наглядностью и широко применяются на практике. В данном курсе изучаются следующие аксонометрические проекции: изометрическая проекция, имеющая единый масштаб для всех трех осей расположенных под углом 120° друг к другу (рис.19,а) и фронтальная диметрическая, имеющая коэффициент искажения по оси У К = 1:2 и оси, расположенные в соответствии с рисунком 19,б. Построение аксонометрических проекций плоских геометрических фигур показаны на рисунке 20.

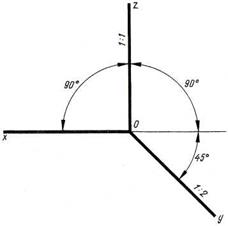
а) Рис.19 б)
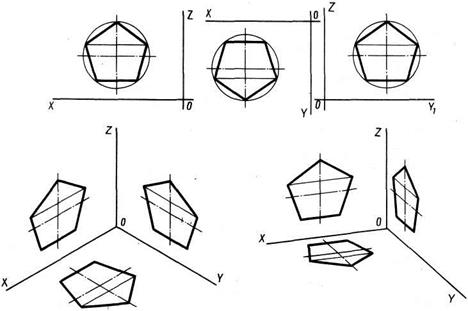
а)

б)
Рис.20
Графическая работа №5
Наименование работы «Проекции группы тел».
Формат А3.
Содержание работы: построение комплексного чертежа и изометрической проекции группы геометрических тел.
Методические указания.
При выполнении работы необходимо учесть, что при построении аксонометрии одного геометрического тела оси симметрии и аксонометрические оси совмещают. При построении группы тел необходимо принять одно из тел за главное или совместить аксонометрические оси с центром осей координат. Построение аксонометрии группы тел вести поэтапно (полностью выполнив проекцию одного тела, приступать к другому).
На комплексном чертеже линии невидимого контура указать штриховой линией.
Варианты заданий к выполнению данной графической работы и образец выполнения даны в приложении 7.
Многие детали, элементы строительных конструкции имеют различные срезы, поэтому необходимо выработать умения их построения в ортогональных проекциях и в аксонометрии, а также научиться строить развертки усеченных геометрических тел.
Графическая работа № 6
Наименование работы «Развертка усеченного геометрического тела».
Формат А3.
Содержание работы: построение трех проекций усеченного цилиндра, натуральной величины сечения, развертки и изометрии.
Методические указания
При построении геометрических тел со срезамиусловимся, что отсеченная плоскостью часть геометрического тела отбрасывается, а оставшаяся часть геометрического тела ограничена контуром сечения. Сечением называется плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхностям тела, так и секущей плоскости. Таким образом, задача на построение сечения сводится к построению точек пересечения прямых (образующих) с секущей плоскостью.
Построение натуральной величины сечения выполнить способом замены плоскостей проекций.
Пример выполнения задания, и таблица исходных данных по вариантам даны в приложении 8.
2.3 Проекции модели. Простые разрезы.
Графическая работа №7
Наименование работы «Проекции модели».
Формат А3.
Содержание работы: по двум заданным проекциям модели построить третью и аксонометрическую.
Методические указания
Построение вести методом ортогонального проецирования, т. е. все три проекции строить без нарушения проекционной связи, но оси координат и линии проекционной связи не проводить. Сначала изучают конструкцию модели, мысленно разделяя ее на простые элементы (геометрические тела). Построение ведут в тонких линиях, а закончив, проставляют размеры и обводят.
Пример выполнения и варианты задания даны в приложении 9.
В конструкции модели могут быть отверстия, прорези, углубления. Их очертания, выполненные линиями невидимого контура, усложняют чертеж. Избежать этого можно применением разрезы. Разрез – это изображение предмета, мысленно рассеченного плоскостью. При этом, часть предмета, находящуюся между человеком и секущей плоскостью, мысленно удаляют. Секущая плоскость указана разомкнутой линией, стрелкой – направление взгляда.






