Явление наведения э.д.с. в каком-либо контуре при изменении тока в другом контуре называется явлением взаимной индукции.
Рассмотрим два контура, расположенные на некотором расстоянии друг от друга. Предположим, что ток 
протекает только в первом контуре. Линии магнитной индукции, сцепляющиеся с этим контуром, образуют потокосцепление самоиндукции 
, а те из них, которые сцепляются со вторым контуром, определяют потокосцепление взаимной индукции 
. Если ток 
протекает только по второму контуру (
), то можно аналогично ввести понятия 
-потокосцепление самоиндукции второго контура и 
- потокосцепление взаимной индукции первого контура, создаваемое током во втором контуре.
При протекании токов в обоих контурах справедливы равенства
где 
и 
- полные потокосцепления первого и второго контуров. В этих соотношениях ставят знак "+", если поток взаимной индукции совпадает по направлению с потоком самоиндукции (согласное включение контуров) и знак " -" в противоположном случае (встречное включение).
Если сердечники катушек выполнены из материала с постоянной магнитной проницаемостью, то потокосцепление пропорционально 
, а потокосцепление пропорционально току 
. Коэффициенты пропорциональности обозначают буквой 
с соответствующими индексами и называют взаимной индуктивностью контуров:
На основе закона сохранения энергии можно показать, что взаимные индуктивности 
и 
равны друг другу: 
.
Для характеристики степени магнитной связи двух катушек вводят также безразмерный параметр, который носит название коэффициента связи:
Важным свойством коэффициента связи является его ограниченность 
, при этом нулевое значение коэффициента означает отсутствие магнитной связи между катушками.
Взаимная индуктивность характеризует связь между двумя контурами за счет общего магнитного поля и зависит от взаимного расположения контуров, в частности от расстояния между ними и от их взаимной ориентации. Очевидно, что при увеличении расстояния между катушками и при сохранении их взаимной ориентации величина взаимной индуктивности будет уменьшаться, так как интенсивность магнитного поля, создаваемого контуром с током, уменьшается с увеличением расстояния от него. Зависимость взаимной индуктивности от ориентации контуров наглядно иллюстрируется на рисунке.
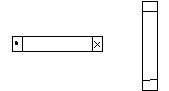Несмотря на близость двух контуров, линии индукции магнитного поля, создаваемого током в первом контуре, не пересекают плоскость второго, следовательно, взаимная индуктивность контуров равна нулю.
На величину взаимной индуктивности оказывает влияние также магнитная проницаемость объектов, находящихся в непосредственной близости от контуров. В частности, ферромагнитные тела могут существенно искажать картину магнитного поля, что в свою очередь может изменить (как увеличить, так и уменьшить) взаимную индуктивность контуров.
Э.д.с, наводимая в контуре, согласно закону электромагнитной индукции, определится соотношением
Тогда напряжение, приложенное к первому контуру, может быть записано в виде:
По аналогии, для приложенного ко второму контуру напряжения, имеем
При изменении токов по синусоидальному закону связь между токами и напряжениями определяется аналогичными соотношениями для комплексных величин
Взаимная индуктивность может быть как положительной величиной так и отрицательной. Принято считать, что > 0, если при протекании в катушках токов, направления которых условно приняты за положительные, потоки взаимной индукции совпадают по направлению с потоками самоиндукции, и < 0 в противном случае. Очевидно, что знак взаимной индуктивности зависит как от взаимного расположения контуров, так и от тех направлений токов, которые приняты за положительные.
Часто один из выводов каждой из индуктивно связанных катушек маркируют специальными значками, например, звездочками (*). Положительными направлениями токов в таком случае считаются направления токов от звездочки.
При таком определении знаков взаимной индуктивности можно сформулировать следующее правило для определения направления напряжения взаимной индукции: если в одной катушке положительное направление тока принято от звездочки, то положительное направление напряжения взаимной индукции на другой катушке также будет направлено от звездочки, и наоборот.
Рассмотрим две индуктивно связанные катушки, размещенные на одном сердечнике (рис. 9.1)
Промаркируем катушки произвольным образом, так как это показано на рис. 9.1а. Учитывая направление намотки и маркировку катушек, можем определить знак взаимной индуктивности. Если токи в катушках направить от звездочек, то их потоки совпадут по направлению, а это значит, что взаимная индуктивность положительна.
При другом варианте маркировки (рис. 9.1б) получаем 
. Таким образом, маркировка катушек и знак на схеме однозначно определяют взаимные направления реальных магнитных потоков катушек, присутствующих в электрической цепи.
Рассмотрим две схемы (рис. 9.2) последовательного соединения этих катушек с маркировкой, указанной на рис. 9.1а
В зависимости от соединения катушек - согласного (рис. 9.2а) или встречного (рис. 9.2б), будет изменяться вид уравнений, описывающих режим работы схемы.
Рассмотрим случай согласного включения катушек. Запишем уравнение второго закона Кирхгофа в комплексной форме
Падение напряжения на первой катушке складывается из двух составляющих - падения напряжения 
, совпадающего с направлением тока, и падения напряжения взаимной индукции от тока, протекающего во второй катушке 
. Для определения направления напряжения взаимной индукции обратим внимание на то, что ток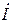 
протекает по второй катушке от звездочки. Это означает, что соответствующее падение напряжения 
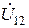, приложенное к первой катушке, также будет направлено от звездочки. Это направление совпадает с направлением обхода контура, и поэтому соответствующее слагаемое войдет в уравнение со знаком "+". Проведя аналогичный анализ для падения напряжения на второй катушке, получим, уравнение
или
Величина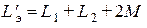 
представляет собой эквивалентную индуктивность всей цепи. Эквивалентная индуктивность — величина сугубо положительная, что следует из выражения для энергии магнитного поля
Переход от согласного включения к встречному может быть осуществлен путем пересоединения концов обмотки одной из катушек (рис. 9.2 б). Уравнение второго закона Кирхгофа для этого случая отличается от предыдущего тем, что падения напряжения взаимной индукции входят в уравнение со знаком "-". Действительно, ток во второй катушке теперь направлен к звездочке. Это означает, что соответствующее падение напряжения на первой катушке 
будет направлено к звездочке и не совпадает с направлением обхода контура. Точно также падение напряжения 
направлено в сторону, противоположную направлению обхода контура и, следовательно, войдет в уравнение со знаком "-"
или
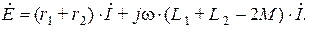
Эквивалентная индуктивность системы из двух катушек в этом случае равна
Как и в предыдущем случае, эта индуктивность больше нуля.
Изменение величины эквивалентной индуктивности при пересоединении концов обмотки одной из катушек может быть использовано на практике для определения величины взаимной индуктивности:
На рисунке 9.3 показаны векторные диаграммы для согласного (а) и встречного (б) включений катушек при одинаковом значении тока в обоих случаях.
Построение векторной диаграммы для случая (а) начнем с вектора тока 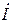. Затем отложим вектора падений напряжения на резисторе 
, катушке индуктивности 
, резисторе 
, катушке индуктивности 
. Вектора напряжений взаимной индукции 
будут совпадать по направлению с векторами напряжений самоиндукции 
и 
в соответствии с правилом, сформулированным выше. Сложив вектора, соответствующие всем падениям напряжений, получим вектор э.д.с. 
, действующей в контуре.
Векторная диаграмма для случая (б) строится в той же последовательности, однако теперь вектора напряжений взаимоиндукции противоположны по направлению векторам напряжения самоиндукции и .
В качестве примера более сложной задачи рассмотрим формирование уравнений Кирхгофа для цепи, изображенной на рис. 9.4. Взаимное влияние катушек друг на друга учитывается маркировкой и величинами взаимных индуктивностей 
, 
, 
.
Условно положительные направления токов в ветвях показаны стрелками. В соответствии с первым законом Кирхгофа можем сформировать одно уравнение
Для формирования уравнений второго закона Кирхгофа выберем независимые контура и зададим направление их обхода так, как это показано на рисунке. Рассматривая контур с источником э.д.с., заметим, что падение напряжения на катушке индуктивности складывается из трех составляющих: падения напряжения 
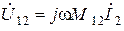от тока, протекающего в этой катушке и напряжений взаимной индукции 
и 
. Слагаемое 
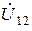войдет в уравнение со знаком "+", так как ток 
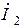направлен в катушке индуктивности к звездочке, следовательно, напряжение взаимной индукции будет также направлено к звездочке и совпадает с направлением обхода контура. Во втором случае ток 
направлен в катушке от звездочки, он создает падение напряжения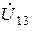 
на катушке от звездочки, направленное противоположно обходу контура, и соответствующее падение напряжения войдет в уравнение со знаком "-".
Проведя аналогичные рассуждения для определения знаков напряжений на катушках 
и 
, запишем уравнения второго закона Кирхгофа:
