“Теоретическая кривая никогда не проходит в точности через все точки, полученные в результате измерений…” В. Фукс [1975].
Рассчитать уравнение регрессии не представляет особой сложности, особенно при наличии компьютера с установленным табличным процессором Microsoft Excel, или любого другого пакета статистических программ. Основные методологические трудности возникают в ходе проверки выполнения априорных предпосылок регрессионного анализа и последующей оценки адекватности полученного уравнения.
Парная (однофакторная) регрессия является частным случаем множественной регрессии. Схематически модель множественной регрессии записывается в виде: 
, где y – результативный экономический показатель, x 1, x 2, …, xn – входные факторы.
Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функций издержек производства, в макроэкономических расчетах и при решении других вопросов в различных экономических сферах. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике.
Основная цель множественной регрессии – построение модели с большим числом факторов и определение влияния каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель y.
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели (выбор факторов, вида уравнения и др.)
Отбор факторов регрессионной модели. Факторы, включаемые в модель множественной регрессии, должны отвечать следующим требованиям:
· должны быть количественно измеримы;
· не должны быть интеркоррелированы[1] или находится в функциональной зависимости;
· в одну модель нельзя включать совокупный фактор и образующие его частные факторы, что может привести к неоправданному увеличенному их влияние на зависимый показатель, к искажению реальной действительности;
· количество включаемых в модель факторов не должно превышать одной трети числа наблюдений в выборке.
Отбор факторов для регрессионной модели обычно осуществляется в две стадии: на первой подбираются факторы, исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют t - статистики для параметров регрессии.
Коэффициенты интеркорреляции позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если коэффициент интеркорреляции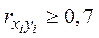 
.
Из двух явно коллинеарных факторов, из уравнения регрессии рекомендуется исключить один. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
Пример. для зависимости 
в таблице 12 задана матрица парных коэффициентов корреляции.
Т а б л и ц а 12
| y | x 1 | x 2 | x 3 | |
| y | ||||
| x 1 | 0,8 | |||
| x 2 | 0,7 | 0,8 | ||
| x 3 | 0,6 | 0,5 | 0,2 |
Из таблицы очевидно, что факторы x 1 и x 2коррелированны друг с другом. В уравнение регрессии целесообразно включить фактор x 2, а не x 1, так как корреляция x 2 с y – слабее, чем корреляция фактора x 1 с y 
, но зато 
. Поэтому в уравнение множественной регрессии включаются факторы x 2 и x 3.
Этапы построения регрессионной модели. Двумя наиболее важными этапами построения многофакторных моделей являются:
· выбор формы связи (уравнения регрессии);
· отбор факторных признаков.
На первом этапе построения РМ производится выбор вида (структуры) уравнения регрессии. Наиболее приемлемым способом выбора формы связи, то есть вида исходного уравнения, является метод перебора различных уравнений. При этом значительное число различных уравнений регрессии реализуется на ЭВМ с помощью специально разработанного алгоритма перебора с последующей статистической проверкой (обычно на основе t-критерия Стьюдента).
Уравнения как парной так и множественной регрессии могут быть линейными и нелинейными.
Наиболее часто используются линейная и степенная функции:
– линейная,
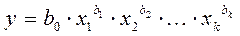– степенная.
широко применяются и следующие уравнения множественной регрессии:
– экспоненциального вида,
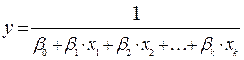– гиперболического вида.
В качестве уравнений множественной регрессии могут быть использованы и другие виды математических функций.
После выбора формы связи определяются неизвестные коэффициенты модели, для чего чаще всего используется широко известный метод наименьших квадратов (МНК).
При нелинейной форме связи для определения коэффициентов могут быть использованы два подхода:
1) когда нелинейная форма связи представляется в виде линеаризованной функции; при котором исследователь сначала выбирает форму нелинейной РМ, а затем ее линеаризует, преобразуя члены уравнения регрессии;
2) когда используется итерационный нелинейный метод наименьших квадратов.
На втором этапе построения уравнения множественной регрессии можно выделить три стадии отбора факторов, включаемых в модель.
· На первой стадии осуществляется априорный анализ и на факторы, включаемые в предварительный состав модели, не накладывается каких-либо особых ограничений.
· На второй (наиболее важной) стадии производится сравнительная оценка и отсев части факторов. Это достигается анализом парных коэффициентов и оценкой их значимости.
· На третьей стадиипроизводят окончательный отбор факторов путем анализа значимости оценок параметров различных вариантов уравнений с использованием критерия Стьюдента.
