Комплексные числа
1.1 Множество C комплексных чисел
Введем традиционные обозначения: R – множество вещественных чисел, R 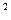 - совокупность всевозможных упорядоченных пар
- совокупность всевозможных упорядоченных пар 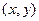 вещественных чисел. Произ- вольный элемент
вещественных чисел. Произ- вольный элемент 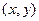 множества R
множества R  обозначим через z:
обозначим через z:  , где
, где 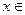 R,
R, 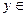 R.
R.
Два элемента 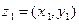 и
и 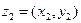 множества
множества  считаем равными, если
считаем равными, если 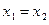 и
и  :
: 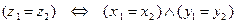 .
.
Введем две операции, одну их которых назовем сложением элементов из R  , а другую – умножением этих элементов. Каждая из них представляет собой правило, в силу которого любой упорядоченной паре
, а другую – умножением этих элементов. Каждая из них представляет собой правило, в силу которого любой упорядоченной паре 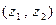 элементов из R
элементов из R 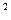 ставится в соот- ветствие некоторый третий элемент этого множества.
ставится в соот- ветствие некоторый третий элемент этого множества.
Элемент, который паре 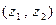 сопоставляет операция сложения, назовем суммой элементов
сопоставляет операция сложения, назовем суммой элементов  и
и  и обозначим через
и обозначим через 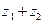 .
.
Элемент, который паре 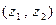 сопоставляет операция умножения, назовем произведением элементов
сопоставляет операция умножения, назовем произведением элементов  и
и  и обозначим через
и обозначим через  или
или  .
.
Сумму и произведение элементов 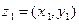 и
и 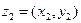 определим с помощью следующих равенств:
определим с помощью следующих равенств:
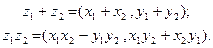 (1)
(1)
Множество всевозможных упорядоченных пар вещественных чисел R 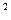 , на котором указанным выше способом введены операции сложения и умножения называ- ют множеством комплексных чисел и традиционно обозначают буквой C. Элементы множества C называют комплексными числами.
, на котором указанным выше способом введены операции сложения и умножения называ- ют множеством комплексных чисел и традиционно обозначают буквой C. Элементы множества C называют комплексными числами.
Нетрудно убедиться, что введенные равенствами (1) операции обладают свойс- твами, аналогичными свойствам сложения и умножения вещественных чисел:
1. (Коммутативность) 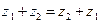 ;
; 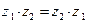 .
.
2. (Ассоциативность) 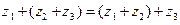 ;
;  .
.
3. (Дистрибутивность) 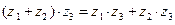 .
.
Наименования операций над комплексными числами – сложение и умножение - обьясняются этими аналогиями.
Таким образом, комплексное число 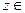 C, представляет собой упорядоченную пару вещественных чисел:
C, представляет собой упорядоченную пару вещественных чисел:  . Первое число x пары
. Первое число x пары 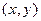 называют вещест- венной частью комплексного числа z и обозначают через
называют вещест- венной частью комплексного числа z и обозначают через 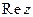 , второе число y этой пары называют мнимой частью комплексного числа z и обозначают через
, второе число y этой пары называют мнимой частью комплексного числа z и обозначают через 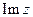 .
.
Пусть мнимые части чисел  и
и  равны нулю:
равны нулю: 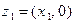 ,
,  . Тогда из (1) получим:
. Тогда из (1) получим:
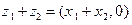 ;
; 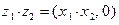 .
.
Заметим, что сложение и умножение комплексных чисел  и
и  , мнимые части которых равны нулю, сводятся соответственно к сложению и умножению их вещественных частей. Это обстоятельство позволяет отождествить комплексное число вида
, мнимые части которых равны нулю, сводятся соответственно к сложению и умножению их вещественных частей. Это обстоятельство позволяет отождествить комплексное число вида  с вещественным числом x, т.е., считать, что
с вещественным числом x, т.е., считать, что 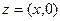 = x. Особо отметим равенство
= x. Особо отметим равенство 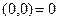 ,а также справедливость следующего утверждения: пусть
,а также справедливость следующего утверждения: пусть  ; равенство
; равенство 
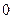 имеет место тогда и только тогда, когда х=
имеет место тогда и только тогда, когда х= 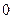 и у=
и у= 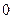 .
.
Комплексное число  , мнимая часть y которого отлична от нуля, назы- вают мнимым. Следовательно, всякое комплексное число является либо вещественным, либо мнимым.
, мнимая часть y которого отлична от нуля, назы- вают мнимым. Следовательно, всякое комплексное число является либо вещественным, либо мнимым.
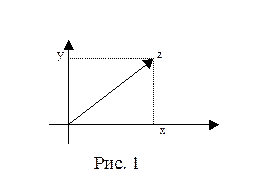 Остановимся на геометрических ин- терпретациях множества C. Как известно, геометрической интерпретацией множества R
Остановимся на геометрических ин- терпретациях множества C. Как известно, геометрической интерпретацией множества R  является плоскость с введенной на ней декартовой прямоугольной системой коор- динат: упорядоченная пара
является плоскость с введенной на ней декартовой прямоугольной системой коор- динат: упорядоченная пара 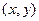 изобража- ется точкой плоскости с абсциссой x и орди- натой y. Эту же точку плоскости считают изображением комплексного числа
изобража- ется точкой плоскости с абсциссой x и орди- натой y. Эту же точку плоскости считают изображением комплексного числа  . Когда точки плоскости рассматривают как изображения комплексных чисел, саму плоскость считают интерпретацией множества С и называют комплексной плоскостью. Изображениями комплексных чисел вида
. Когда точки плоскости рассматривают как изображения комплексных чисел, саму плоскость считают интерпретацией множества С и называют комплексной плоскостью. Изображениями комплексных чисел вида  , т.е., вещественных чисел, будут точки оси абсцисс; поэтому ее называют веще- ственной осью комплексной плоскости. Мнимые числа вида
, т.е., вещественных чисел, будут точки оси абсцисс; поэтому ее называют веще- ственной осью комплексной плоскости. Мнимые числа вида 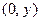 ,
, 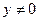 , изобража- ются точками оси ординат; эту ось называют мнимой осью комплексной плоскости (рис. 1).
, изобража- ются точками оси ординат; эту ось называют мнимой осью комплексной плоскости (рис. 1).
Другая возможная геометрическая интерпретация комплексного числа  состоит в том, что его изображают вектором, проекции которого на вещественную и мнимую оси есть x и y соответственно. В частности, в качестве изображения числа
состоит в том, что его изображают вектором, проекции которого на вещественную и мнимую оси есть x и y соответственно. В частности, в качестве изображения числа  может выступать радиус-вектор точки с абсциссой x и ординатой y (рис. 1). Такой взгляд на комплексное число удобен в ряде случаев, например, при геометриче- ской интерпретации действий сложения и вычитания комплексных чисел (см. ниже).
может выступать радиус-вектор точки с абсциссой x и ординатой y (рис. 1). Такой взгляд на комплексное число удобен в ряде случаев, например, при геометриче- ской интерпретации действий сложения и вычитания комплексных чисел (см. ниже).
1.2. Алгебраическая форма комплексного числа.
Среди комплексных чисел особая роль принадлежит мнимому числу 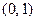 . Его называют мнимой единицей и обозначают обычно буквой i: i =
. Его называют мнимой единицей и обозначают обычно буквой i: i = 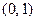 . Это название связано с равенством
. Это название связано с равенством 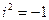 . Действительно, вычислив произведение
. Действительно, вычислив произведение 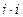 в соответ- ствии со вторым из равенств (1) получим:
в соответ- ствии со вторым из равенств (1) получим:
 .
.
Пусть  – некоторое комплексное число. Используя (1), нетрудно убе- диться в справедливости равенства
– некоторое комплексное число. Используя (1), нетрудно убе- диться в справедливости равенства  . Но
. Но 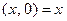 ,
, 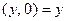 ,
, 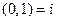 ; поэтому равенство
; поэтому равенство  можно переписать так:
можно переписать так: 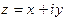 . Правую часть последнего равенства называют алгебраической формой комплексного числа
. Правую часть последнего равенства называют алгебраической формой комплексного числа  .
.
Пусть заданы комплексные числа 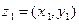 и
и 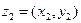 . Из равенств (1) вытекают правила сложения и умножения комплексных чисел, записанных в алгеб- раической форме: если
. Из равенств (1) вытекают правила сложения и умножения комплексных чисел, записанных в алгеб- раической форме: если 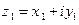 ,
, 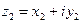 , то
, то
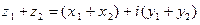 ;
; 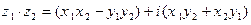 . (2)
. (2)
Отметим три свойства этих действий. Они дополняют свойства 1 – 3, указанные в п. 1.1 и тоже вполне аналогичны соответствующим свойствам действий над вещест- венными числами.
4. 
 ,
, 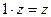 .
.
 Запишем числа
Запишем числа 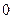 и z в алгебраической форме:
и z в алгебраической форме:  ,
, 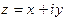 . Из (1) получим:
. Из (1) получим: 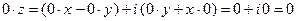 . Доказательство второго равен- ства аналогично.
. Доказательство второго равен- ства аналогично. 
5. Пусть  и
и  – некоторые комплексные числа. Для того, чтобы произве- дение
– некоторые комплексные числа. Для того, чтобы произве- дение  было равно нулю, необходимо и достаточно, чтобы хотя бы один из мно- жителей
было равно нулю, необходимо и достаточно, чтобы хотя бы один из мно- жителей  и
и  был равен нулю:
был равен нулю:
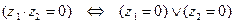 .
.
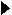 Необходимость. Пусть
Необходимость. Пусть 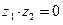 . Покажем, что если один из множителей отличен нуля, то другой должен равняться нулю. Пусть, например,
. Покажем, что если один из множителей отличен нуля, то другой должен равняться нулю. Пусть, например, 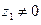 ; покажем, что тогда
; покажем, что тогда 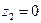 . Действительно, запишем эти числа в алгебраической форме:
. Действительно, запишем эти числа в алгебраической форме: 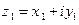 ,
, 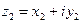 . Из (1) имеем:
. Из (1) имеем: 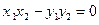 и
и 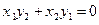 . Отсюда сле- дует, что числа
. Отсюда сле- дует, что числа 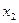 и
и 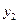 удовлетворяют однородной системе
удовлетворяют однородной системе
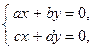 где
где  ,
, 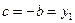 . Определитель D этой системы отличен от нуля: так как
. Определитель D этой системы отличен от нуля: так как  , то
, то 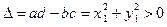 . Значит, система имеет только нулевое решение:
. Значит, система имеет только нулевое решение: 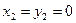 ; поэтому
; поэтому 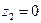 .
.
Следовательно, из 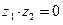 вытекает, что либо
вытекает, что либо 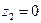 , либо
, либо 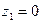 .
.
Достаточность очевидна в силу свойства 4. 
6. Пусть  и
и  – комплексные числа. Тогда
– комплексные числа. Тогда
 .
.
 Пусть
Пусть 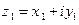 ,
, 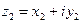 . Тогда
. Тогда
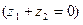 Û
Û 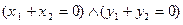
 .
.
Отсюда:
 .
. 
Пусть z Î C. Число (–1) z обозначают через – z и называют числом, проти- воположным z. Из свойства 6 следует: сумма числа z и числа противоположного z равна нулю: " z Î C z + (– z) = 0.
Вычитание комплексных чисел вводится как операция, обратная сложению: пусть  и
и  – заданные числа; разностью чисел
– заданные числа; разностью чисел  и
и  называют число z такое, что
называют число z такое, что 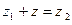 ; разность чисел
; разность чисел  и
и  обозначают через
обозначают через 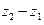 .
.
Запишем  ,
,  и z в алгебраической форме:
и z в алгебраической форме: 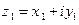 ,
, 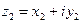 ,
, 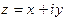 . Имеем:
. Имеем:
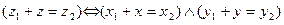 . Отсюда:
. Отсюда:
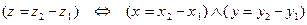 , так что к правилам сложения и умножения (2) можно добавить правило вычитания:
, так что к правилам сложения и умножения (2) можно добавить правило вычитания:
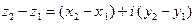 . (3)
. (3)
Заметим, что равенства (2) и (3) можно получить складывая, перемножая и вычитая двучлены 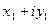 и
и 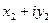 по правилам алгебры, известным из школьных учебников; при перемножении этих двучленов используется равенство
по правилам алгебры, известным из школьных учебников; при перемножении этих двучленов используется равенство 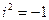 . Следовательно, складывая, вычитая, умножая, возводя в натуральную степень комп- лексные числа, записанные в алгебраической форме, можно руководствоваться правилами алгебры, изложенными в школьных учебниках, учитывая при этом значения степеней числа i:
. Следовательно, складывая, вычитая, умножая, возводя в натуральную степень комп- лексные числа, записанные в алгебраической форме, можно руководствоваться правилами алгебры, изложенными в школьных учебниках, учитывая при этом значения степеней числа i:  ,
, 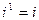 ,
, 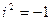 ,
, 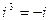 ,
, 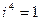 и т. д. В частности, можно применять формулы сокращенного умножения.
и т. д. В частности, можно применять формулы сокращенного умножения.
Пример 1. Найдём алгебраическую форму числа  .
.
Число 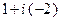 запишем в виде двучлена
запишем в виде двучлена  и воспользуемся формулой
и воспользуемся формулой 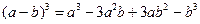 . Получим:
. Получим:
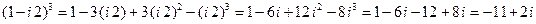 .
.
Деление комплексных чисел вводится как операция, обратная умножению: пусть  и
и  – комплексные числа, причем
– комплексные числа, причем 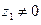 ; частным чисел
; частным чисел  и
и  называют число z такое, что
называют число z такое, что 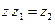 ; обозначают это число символами
; обозначают это число символами 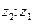 и
и  . Запишем числа
. Запишем числа  ,
,  и z в алгебраической форме:
и z в алгебраической форме: 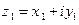 ,
, 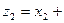
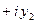 ,
, 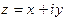 ; тогда из
; тогда из 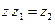 следует:
следует: 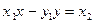 ,
, 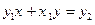 . Эти два равенства рассмотрим как систему двух линейных относительно x и y уравнений. Определитель D этой системы равен
. Эти два равенства рассмотрим как систему двух линейных относительно x и y уравнений. Определитель D этой системы равен 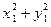 ; так как
; так как  , то и
, то и  ; поэтому система имеет единственное решение, которое можно найти по формулам Крамера:
; поэтому система имеет единственное решение, которое можно найти по формулам Крамера:
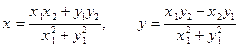 ..Таким образом,
..Таким образом,
 . (4) Выполняя деление
. (4) Выполняя деление 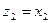
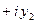 на
на 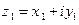 , обычно прибегают к следующему приему: числитель и знаменатель дроби
, обычно прибегают к следующему приему: числитель и знаменатель дроби  умножают на двучлен
умножают на двучлен 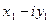 (число
(число 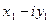 называют сопряженным числу
называют сопряженным числу 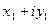 , см. ниже 1.7):
, см. ниже 1.7):
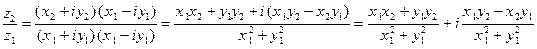 .
.
Пример 2. Вычислить 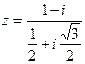 .
.
Имеем:
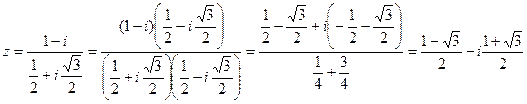 .
. 
 В заключение этого пункта оста- новимся на геометрической интерпрета- ции суммы
В заключение этого пункта оста- новимся на геометрической интерпрета- ции суммы 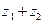 и разности
и разности 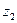
 . Будем изображать комплексные числа векторами, лежащими на комплексной плоскости. Число
. Будем изображать комплексные числа векторами, лежащими на комплексной плоскости. Число 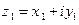 изобразит- ся радиусом-вектором точки
изобразит- ся радиусом-вектором точки  , число
, число 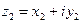 – радиусом-вектором точки
– радиусом-вектором точки  . Число
. Число 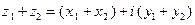 изобразится вектором, проекции которого на оси равны
изобразится вектором, проекции которого на оси равны 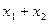 и
и 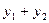 . Из векторной алгебры известно, что такой вектор является суммой векторов
. Из векторной алгебры известно, что такой вектор является суммой векторов  и
и  , т.е. диагональю параллелограмма, построенного на векторах
, т.е. диагональю параллелограмма, построенного на векторах  и
и  (рис. 2). Разность
(рис. 2). Разность 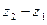
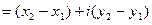 представлена на этом рисунке разностью радиусов-векторов точек
представлена на этом рисунке разностью радиусов-векторов точек  и
и  , т.е. второй диагональю параллелограмма.
, т.е. второй диагональю параллелограмма.
1.3. Модуль комплексного числа
Модулем комплексного числа 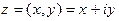 называют вещественное число
называют вещественное число  . Модуль числа z обозначаем через
. Модуль числа z обозначаем через 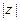 ; таким образом,
; таким образом, 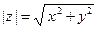 , где
, где 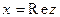 ,
, 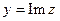 . Если z является вещественным числом, т.е., если
. Если z является вещественным числом, т.е., если  , его модуль совпадает с абсолютной величиной числа x:
, его модуль совпадает с абсолютной величиной числа x: 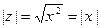 .
.
Геометрический смысл модуля числа  очевиден:
очевиден: 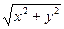 есть расстояние от начала координат до точки
есть расстояние от начала координат до точки  , изображающей число z, или длина вектора, проекции которого на оси есть x и y.
, изображающей число z, или длина вектора, проекции которого на оси есть x и y.
Замечание 1. Разность  изображается вектором, начало которого есть точка
изображается вектором, начало которого есть точка  комплексной плоскости, а концом является
комплексной плоскости, а концом является  (рис.2); значит, модуль разно- сти, число |
(рис.2); значит, модуль разно- сти, число |  |, есть длина этого вектора, т.е. расстояние между точками комплекс- ной плоскости
|, есть длина этого вектора, т.е. расстояние между точками комплекс- ной плоскости  и
и  .
.
Отметим рядсвойств модуля. Они аналогичны свойствам абсолютной величины вещественного числа.
1. Для всякого z Î C его модуль 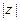 есть неотрицательное число, причем
есть неотрицательное число, причем 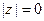 тогда и только тогда, когда
тогда и только тогда, когда  .
.
2. Для всякого z Î C 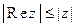 ,
, 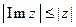 .
.
Справедливость этих утверждений очевидна.
3. Для любых  и
и 
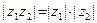 ; если
; если 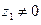 , то
, то 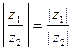 .
.
 Запишем числа
Запишем числа  и
и  в алгебраической форме:
в алгебраической форме: 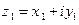 ,
, 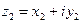 ; тогда (см. (2)):
; тогда (см. (2)):
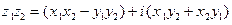 ;
;
 .
.
Пусть 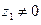 , и пусть
, и пусть 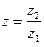 ; тогда
; тогда  . По доказанному выше,
. По доказанному выше, 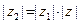 ; отсюда, поскольку здесь все числа вещественные,
; отсюда, поскольку здесь все числа вещественные,  .
. 
4. Для любых комплексных  и
и  справедливы неравенства
справедливы неравенства
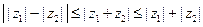 .
.
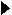 Докажем сначала неравенство
Докажем сначала неравенство 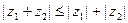 .
.
Справедливость его очевидна в случае 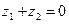 . Пусть
. Пусть 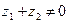 . Обо- значим:
. Обо- значим: 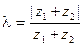 . Отсюда
. Отсюда  ; таким образом, сумма
; таким образом, сумма 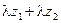 является вещественным и притом положительным числом, в силу чего сумма
является вещественным и притом положительным числом, в силу чего сумма 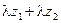 равна сумме вещественных частей слагаемых
равна сумме вещественных частей слагаемых 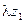 и
и 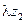 :
:
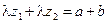 , где
, где 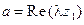 ,
, 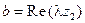 . Так как
. Так как 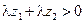 , можем записать:
, можем записать: 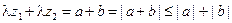 ; эдесь зак- лючительное неравенство вытекает из свойств абсолютной величины вещественных чисел. Из свойств 2 и 3 модуля следует:
; эдесь зак- лючительное неравенство вытекает из свойств абсолютной величины вещественных чисел. Из свойств 2 и 3 модуля следует:
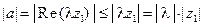 ;
; 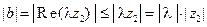 . Таким образом,
. Таким образом, 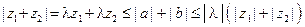 , и так как (см. свойство 3)
, и так как (см. свойство 3) 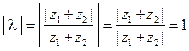 , то окончательно получим:
, то окончательно получим:
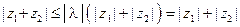 .
.
Докажем неравенство 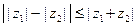 .
.
Это неравенство очевидно, если 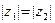 . Пусть
. Пусть  ; тогда
; тогда
 . По доказанному выше
. По доказанному выше  . Значит,
. Значит,
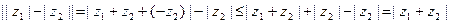 . Случай
. Случай 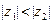 рассматривается аналогично.
рассматривается аналогично. 
Замечание 2. Неравенство 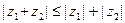 назывют неравенством треуголь- ника, поскольку на него можно смотреть как на неравенство, связывающее длины сторон треугольника, вершинами которого являются точки
назывют неравенством треуголь- ника, поскольку на него можно смотреть как на неравенство, связывающее длины сторон треугольника, вершинами которого являются точки 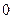 ,
,  и
и 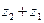 (рис. 2).
(рис. 2).
Упражнение. Используя метод математической индукции, доказать обобщение неравенства треугольника: пусть 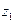 ,
,  , ¼,
, ¼, 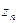 – заданные комплексные числа; тогда
– заданные комплексные числа; тогда
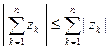 .
.
1.4. Аргумент комплексного числа. Тригонометрическая
форма комплексного числа
Аргументом комплексного числа z, 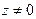 , называют вещественное число j такое, что
, называют вещественное число j такое, что
 , (5) где
, (5) где 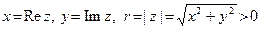
 Если некоторое число j удовлетво- ряет равенствам (5), то им удовлетворит и любое число вида j + 2 k p, k Î Z, причем множество {j + 2 k p}, где k принимает всевозможные целые значения, есть сово- купность всех чисел, удовлетворяющих (5). Таким образом, аргумент числа z имеет бесконечное множество значений, которые отличаются одно от другого слагаемым, кратным 2p. В дальнейшем через
Если некоторое число j удовлетво- ряет равенствам (5), то им удовлетворит и любое число вида j + 2 k p, k Î Z, причем множество {j + 2 k p}, где k принимает всевозможные целые значения, есть сово- купность всех чисел, удовлетворяющих (5). Таким образом, аргумент числа z имеет бесконечное множество значений, которые отличаются одно от другого слагаемым, кратным 2p. В дальнейшем через 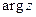 мы обозначаем какое-либо одно из значений аргумента числа z. Равенство
мы обозначаем какое-либо одно из значений аргумента числа z. Равенство 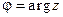 означает, что число j есть одно из значений аргумента числа z. Неравенства
означает, что число j есть одно из значений аргумента числа z. Неравенства  означают, что в данном случае
означают, что в данном случае 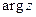 есть то единственное значение аргумента z, которое лежит на промежутке
есть то единственное значение аргумента z, которое лежит на промежутке  ; иногда такое число называют главным значением аргумента z.
; иногда такое число называют главным значением аргумента z.
Геометрически число j, удовлетворяющее условиям (1), есть угол между поло- жительным направлением вещественной оси и вектором z. Если j 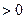 , угол отсчиты- вается от вещественной оси против часовой стрелки, если же j < 0 – угол отсчитыва- ется по часовой стрелке (рис.3).
, угол отсчиты- вается от вещественной оси против часовой стрелки, если же j < 0 – угол отсчитыва- ется по часовой стрелке (рис.3).
Пусть 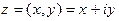 – отличное от нуля комплексное число,
– отличное от нуля комплексное число, 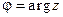 ,
, 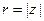 . Учитывая равенства (5), можем записать:
. Учитывая равенства (5), можем записать:
 . Здесь
. Здесь 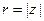 ,
, 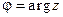 (
( - одно из значений аргумента z, любое).
- одно из значений аргумента z, любое).
Выражение 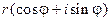 называют тригонометрической формой числа z.
называют тригонометрической формой числа z.
Пример 3. Найдём тригонометрическую форму числа 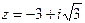 .
.
Имеем: 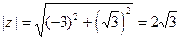 ;
;  .
.
Последнее выражение уже является тригонометрической формой z. Найдём 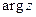 . Равенства (5) в рассматриваемом случае выглядят так:
. Равенства (5) в рассматриваемом случае выглядят так:
 ,
, 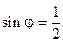 . Отсюда:
. Отсюда: 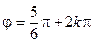 , k Î Z. Взяв в качестве
, k Î Z. Взяв в качестве 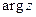 , например, число
, например, число 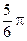 , получим представ- ление числа z в тригонометрической форме, в котором явно фигурирует и модуль, и аргумеит z:
, получим представ- ление числа z в тригонометрической форме, в котором явно фигурирует и модуль, и аргумеит z: 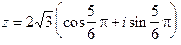 .
.
1.5. Умножение и деление комплексных чисел, записанных
в тригонометрической форме
Пусть отличные от нуля комплексные числа  и
и  записаны в тригонометри- ческой форме:
записаны в тригонометри- ческой форме:
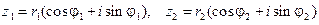 . (6)
. (6)
Найдем тригонометрическую форму произведения  . Заметим, что
. Заметим, что 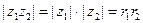 ; кроме того,
; кроме того,
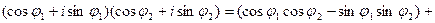
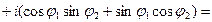
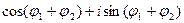 .
.
Отсюда:
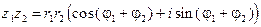 , (7) причем правая часть этого равенства является тригонометрической формой числа
, (7) причем правая часть этого равенства является тригонометрической формой числа 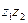 .
.
Итак, при умножении комплексных чисел их модули перемножаются, а аргумен- ты складываются (точнее: сложив аргументы сомножителей, мы получим одно из зна- чений  ). Геометрически умножение числа
). Геометрически умножение числа  на число
на число  сводится к пово- роту вектора
сводится к пово- роту вектора  на угол
на угол  и к изменению длины этого вектора в
и к изменению длины этого вектора в 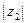 раз.
раз.
Используя (7), с помощью метода математической индукции нетрудно устано- вить справедливость следующего утверждения: пусть 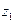 ,
,  , ¼,
, ¼, 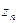 , где n ³ 2, – заданные отличные от нуля числа,
, где n ³ 2, – заданные отличные от нуля числа,  ,
, 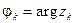 , k = 1, 2, ¼, n; тогда
, k = 1, 2, ¼, n; тогда
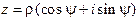 , (8) где
, (8) где 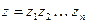 ,
, 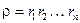 ,
, 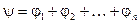 , т.е. при перемножении n, n ³2, комплексных чисел их модули перемножаются, а аргументы складываются.
, т.е. при перемножении n, n ³2, комплексных чисел их модули перемножаются, а аргументы складываются.
Упражнение. Доказать равенство (8).
Найдем частное  , где
, где  и
и  заданы равенствами (6). Заметим (см. п.1.3), что
заданы равенствами (6). Заметим (см. п.1.3), что  . Кроме того,
. Кроме того,

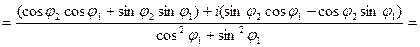
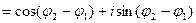 .
.
Значит,
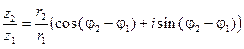 , (9) причем правая часть этого равенства является тригонометрической формой числа
, (9) причем правая часть этого равенства является тригонометрической формой числа  . Таким образом, при делении комплексных чисел их модули делят- ся, а аргументы вычитаются (точнее: вычитая из аргумента числителя аргу- мент знаменателя, мы получим одно из значений аргумента частного).
. Таким образом, при делении комплексных чисел их модули делят- ся, а аргументы вычитаются (точнее: вычитая из аргумента числителя аргу- мент знаменателя, мы получим одно из значений аргумента частного).
Пример 4. Пусть 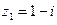 ,
, 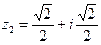 ,
,  . Найти
. Найти  и
и 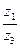 .
.
Запишем заданные числа в тригонометрической форме:
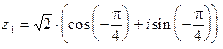 ;
; 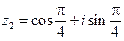 ;
; 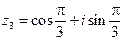 .
.
Таким образом,  ,
, 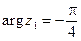 ;
; 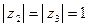 ;
; 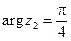 ;
; 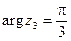 . Теперь получим:
. Теперь получим:
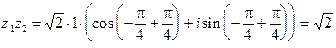 ;
;
 .
.
1.6. Возведение в целую степень и извлечение корня
Пусть 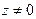 ,
, 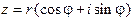 , где r = | z |,
, где r = | z |, 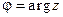 , и пусть n – натуральное число. Степень
, и пусть n – натуральное число. Степень 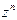 представляет собой произведение n множителей:
представляет собой произведение n множителей:  ; поэтому
; поэтому 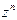 можно вычислить по формуле (8); в рассматриваемом случае
можно вычислить по формуле (8); в рассматриваемом случае 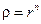 , y = = nj; поэтому
, y = = nj; поэтому
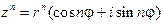 . (10)
. (10)
Определим целые неположительные степени комплексного числа z, z ¹ 0. По определению положим 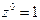 ; и для всякого n, n Î N, по определению положим
; и для всякого n, n Î N, по определению положим 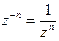 . Заметим: если r = | z |,
. Заметим: если r = | z |, 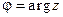 , а n Î N, то
, а n Î N, то
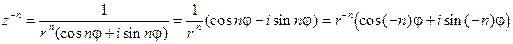 .
.
Таким образом, равенство (10) справедливо при любых целых n. Это равенство называют формулой Муавра; его правая часть представляет собой тригонометрическую форму числа 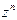 , n Î Z. Заметим, что
, n Î Z. Заметим, что 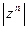 равен
равен  . Если
. Если 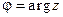 , то n j есть одно из значений
, то n j есть одно из значений 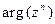 .
.
Пусть заданы комплексное число a и натуральное число n, n ³ 2, и пусть комплексное число z удовлетворяет равенству 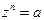 . Тогда z называют корнем степени n из числа a.
. Тогда z называют корнем степени n из числа a.
Если a = 0, то и z = 0 (см. 1.2, свойство 5). Пусть a ¹ 0. Найдем модуль и аргумент числа z. Обозначим: 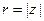 ,
, 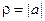 . Из
. Из 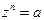 следует
следует  , а из фор- мулы Муавра вытекает
, а из фор- мулы Муавра вытекает 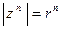 ; значит,
; значит, 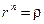 и
и 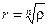 (это “арифметический ” корень:
(это “арифметический ” корень: 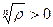 ). Пусть
). Пусть 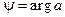 , j = arg z. Тогда {y + 2 k p}, где k Î Z, есть мно- жество всех значений аргумента a; поэтому число n j, будучи одним из значений
, j = arg z. Тогда {y + 2 k p}, где k Î Z, есть мно- жество всех значений аргумента a; поэтому число n j, будучи одним из значений  , должно совпадать с одним из чисел указанного множества. Значит, найдется
, должно совпадать с одним из чисел указанного множества. Значит, найдется 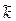 ,
, 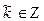 , такое, что
, такое, что  ; тогда
; тогда
 . (11)
. (11)
Пусть k – любое целое число. Обозначим:
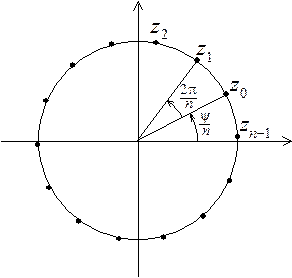 Рис. 4.
Рис. 4.
|
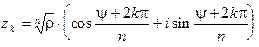 (12) По формуле Муавра получим: " k Î Z
(12) По формуле Муавра получим: " k Î Z 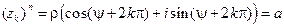 , так что каждое из чисел (12) является корнем степени n из a. С другой стороны, из (11) следует,что всякое число, явля- ющееся корнем степени n из a, содержится среди чисел
, так что каждое из чисел (12) является корнем степени n из a. С другой стороны, из (11) следует,что всякое число, явля- ющееся корнем степени n из a, содержится среди чисел 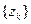 , k Î Z., Значит, множест- во
, k Î Z., Значит, множест- во 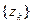 , k Î Z, есть множество всех значений корня степени n из a. Отметим, что в этом мно- жестве имеется всего n попарно различных чисел:
, k Î Z, есть множество всех значений корня степени n из a. Отметим, что в этом мно- жестве имеется всего n попарно различных чисел:  ,
, 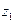 , ¼,
, ¼, 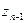 , очевидно, попарно различны, а всякое число
, очевидно, попарно различны, а всякое число 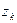 , где k £ –1 или k ³ n, совпа- дает с одним из чисел
, где k £ –1 или k ³ n, совпа- дает с одним из чисел  ,
, 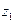 , ¼,
, ¼, 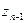 . Таким образом, для вся- кого a Î C, a ¹ 0, имеется ровно n попарно различных значений корня степени n; эти значения можно найти, придавая в формуле (12) ин- дексу k значения 0, 1, 2, ¼, n – 1. Точки комплексной плоскости, изображающие чис- ла
. Таким образом, для вся- кого a Î C, a ¹ 0, имеется ровно n попарно различных значений корня степени n; эти значения можно найти, придавая в формуле (12) ин- дексу k значения 0, 1, 2, ¼, n – 1. Точки комплексной плоскости, изображающие чис- ла  ,
, 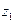 , ¼,
, ¼, 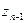 лежат на окружности радиуса
лежат на окружности радиуса 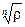 с центром в a = 0 и делят её на n равных дуг (рис.4).
с центром в a = 0 и делят её на n равных дуг (рис.4).
Иногда употребляют символ  для обозначения корня n -й степени из числа a; при a ¹ 0 этот символ имеет n различных значений.
для обозначения корня n -й степени из числа a; при a ¹ 0 этот символ имеет n различных значений.
Пример 5. Положим a = 1 и вычислим корни степени n, где n –нату- ральное число, n ³ 2. Для a = 1 имеем: r = | a | = 1; 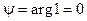 ; значит,
; значит,
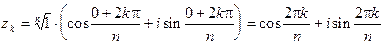 , где k достаточно придавать значения 0, 1, ¼, n – 1. Положив здесь n = 2 и k = 0, 1, найдем два значения корня квадратного из единицы:
, где k достаточно придавать значения 0, 1, ¼, n – 1. Положив здесь n = 2 и k = 0, 1, найдем два значения корня квадратного из единицы:
 ;
; 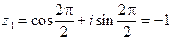 .
.
Положив n = 3 и k = 0, 1, 2, найдем три значения корня кубического из единицы:
 ,
, 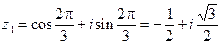 ;
; 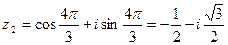 .
.
Эти три точки делят единичную окружность на три равные дуги.
1 .7. Сопряженные комплексные числа
Пусть 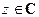 ,
, 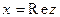 ,
, 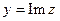 . Обозначим через
. Обозначим через  комплексное число такое, что
комплексное число такое, что 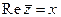 ,
, 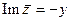 . Таким образом, если
. Таким образом, если 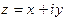 , то
, то 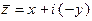 , что обычно записывают в виде разности:
, что обычно записывают в виде разности: 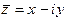 .
.
Каждое из чисел пары z и  называют числом, сопряженным с другим числом этой пары. На комплексной плоскости точки, изображающие числа z и
называют числом, сопряженным с другим числом этой пары. На комплексной плоскости точки, изображающие числа z и  , располагают- ся симметрично относительно вещественной оси.
, располагают- ся симметрично относительно вещественной оси.
Справедливы следующие утверждения.
1. 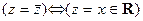 .
.
2 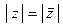 .
.
3. 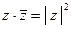 .
.
4. Пусть 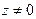 ; если
; если 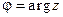 , то число – j является одним из значений аргумента
, то число – j является одним из значений аргумента  .
.
5. 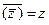 .
.
6. 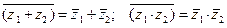 .
.
7. Пусть 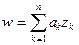 , где
, где 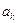 и
и  – комплексные числа; тогда
– комплексные числа; тогда 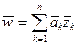 .
.
Упражнение. Доказать перечисленные утверждения.
1.8. Сходящиеся последовательности комплексных чисел
Здесь мы рассматриваем бесконечные последовательности комплексных чисел. Нашей целью является распространение основных понятий и теорем теории последова- тельностей вещественных чисел на более общий случай последовательностей комп- лексных чисел. Последовательность  ,
,  , ¼,
, ¼,  ,.. обозначаем через
,.. обозначаем через 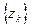 , иногда через
, иногда через 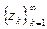 .
.
Сформулированное ниже определение вполне аналогично определению предела последовательности вещественных чисел (гл. 1, п. 3.2).
Пусть заданы последовательность 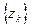 ,
,  , и комплексное число
, и комплексное число  .
.
Определение 1. Число  называют пределом последовательности
называют пределом последовательности 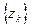 , если для любого положительного числа e существует натуральное число
, если для любого положительного числа e существует натуральное число  такое, что все члены последовательности
такое, что все члены последовательности  , номера k которых превышает
, номера k которых превышает  , удовлетворяют нера- венству
, удовлетворяют нера- венству 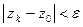 .
.
Если  является пределом последовательности
является пределом последовательности 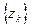 , будем записывать:
, будем записывать: 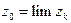 или
или 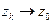 ; саму последовательность
; саму последовательность 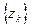 при этом будем называть схо- дящейся последовательностью. Будем также говорить, что последовательность
при этом будем называть схо- дящейся последовательностью. Будем также говорить, что последовательность 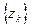 сходится или стремится к
сходится или стремится к  . Таким образом,
. Таким образом, 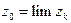 , если
, если
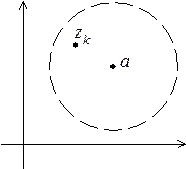 Рис. 5.
Рис. 5.
|
 . (13)
. (13)
Замечание 1. Обозначим: 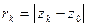 . Тогда
. Тогда 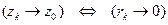 .
.
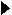 Заменив в (13)
Заменив в (13) 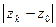 на
на 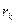 , получим:
, получим:
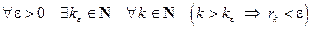 , а это значит, что последовательность вещест- венных чисел
, а это значит, что последовательность вещест- венных чисел 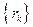 является бесконечно ма- лой. Следовательно, утверждения
является бесконечно ма- лой. Следовательно, утверждения 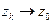 и
и  эквивалентны.◄
эквивалентны.◄
Пусть e – некоторое положительное число, а a – некоторое комплексное число. Множество комплексных чисел z, таких, что  , назовем e- окрест ностью точки a и обозначим через
, назовем e- окрест ностью точки a и обозначим через  :
: 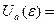 .
. 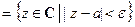 . Геометрически неравенство
. Геометрически неравенство  означает, что расстояние между точками z и a комплексной плоскости меньше e; значит,
означает, что расстояние между точками z и a комплексной плоскости меньше e; значит,






