Погрешности вычислений
Содержание
1.1. Перевод чисел из одной системы счисления в другую.. 2
1.2. Представление чисел в системах с плавающей запятой. 2
1.3. Оценки погрешности. 3
1.4. Машинный эпсилон. 3
1.5. Погрешности вычисления значений функций. 4
1.6. Примеры неустойчивости алгоритмов. 5
1.7. Пример Уилкинсона. 5
1.1. Перевод чисел из одной системы счисления в другую
Перевод десятичной дроби в двоичную систему: последовательное сравнение дроби с 
. Для выполнения этого число 
умножим на 2 и сравним с 1: если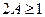 
, в старший разряд двоичной дроби запишем 1, иначе запишем 0. Обозначим дробную часть числа 
буквой 
. Теперь сравним с единицей число 
и запишем в следующий разряд двоичной дроби 1 или 0. Продолжим подобным образом процесс заполнения двоичных разрядов, на каждом шаге умножая на 2 дробную часть числа, полученного на предыдущем шаге.
Пример 1.1. Найдем двоичное представление числа 
. Выполняя описанный алгоритм, находим последовательность чисел:
.
Следовательно, двоичное представление числа имеет вид: 
.
Пример 1.2. Найдем двоичное представление числа 
. Последовательно находим:
.
Далее процесс повторяется. Получаем, что данное число в двоичной системе описывается бесконечной, периодической дробью 
. В скобках записан период дроби. Следовательно, при использовании двоичной дроби конечной длины возникает ошибка округления. Например, 
. При большом количестве знаков ошибка округления мала, но она всегда присутствует.
Представление чисел в системах с плавающей запятой
Представление чисел в системах с плавающей запятой характеризуется четырьмя параметрами:
- основанием
, - длиной мантиссы (точностью)
, - пределами изменения показателей
.
Произвольное число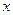 
в системе с плавающей запятой можно представить в виде:
,
где число в круглых скобках – дробная часть – мантисса, p – порядок числа 
.
Система с плавающей запятой называется нормализованной, если для каждого ненулевого числа 
.
Действительные компьютерные реализации могут в деталях отличаться, но эти различия несущественны при обсуждении ошибок округления. Множество чисел в системе с плавающей запятой является конечным. Множество положительных и отрицательных чисел с учетом числа ноль в нормализованной системе равно
.
Числа расположены неравномерно на оси чисел. Рассмотрим пример нормализованной системы:
.
Все возможные дробные части системы – числа, имеющие порядок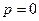 
:
.
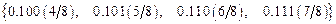Чтобы получить остальные числа системы, нужно умножить эти дроби на 
. Получим числа от 
до 3.5. Все положительные числа системы показаны на рис. 1.1.
Не любое действительное число может быть представлено в такой системе. Сумма чисел, входящих в систему, может не принадлежать системе, даже если эта сумма меньше максимального числа 3.5. В подобной системе не выполняются законы ассоциативности и дистрибутивности.
Рассмотрим пример. Сложим три числа: 
. Рассмотрим два варианта объединения слагаемых: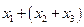 
и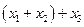 
.
1) 
; прибавив к этому 
, получим точный ответ: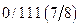 
.
2) 
. Такого числа нет в системе – требуется округление. Возможны два
варианта: округление до большего и округление до меньшего
а) Округляем до большего: 
. Прибавив 
, вновь получаем число, которого нет в системе: 
. Вновь округляя до большего, получаем неверный ответ: сумма равна 1.0.
б) При округлении до меньшего полагаем 
. Прибавив , опять получим число, которого нет в системе: 
. В соответствии с выбранным правилом округления до меньшего отбрасываем последний разряд и вновь получаем неверный результат: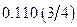 
.
Получили, что в нашей системе от перемены мест слагаемых сумма меняется!
Оценки погрешности
Пусть a – точное значение некоторой величины, a * – ее приближенное значение. Абсолютная погрешность приближенного значения равна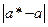 
. Поскольку точное значение a обычно неизвестно, то задача состоит в нахождении оценки абсолютной погрешности 
, которая удовлетворяет неравенству 
– оценка не должна быть меньше истинной погрешности.
Относительная погрешность определяется отношением: 
. Для оценки абсолютной величины относительной погрешности 
должно выполняться неравенство:
.
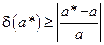Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева. В нормализованной системе все цифры – значащие.
Значащая цифра называется верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.
Машинный эпсилон
Пусть имеется двоичная нормализованная система с t разрядами. Пусть точное значение числа a представляет собой бесконечную двоичную дробь с экспоненциальным множителем:
.
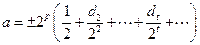Пусть приближенное значение получается в результате усечения – отбрасывания всех разрядов, начиная с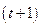 
-го:
, –
тогда абсолютная ошибка равна
.
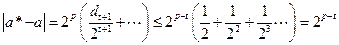В нормализованной системе
.
Следовательно, относительная ошибка удовлетворяет неравенству:
.
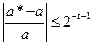Если вместо простого отбрасывания младших разрядов используется округление, то можно считать, что относительная ошибка в два раза меньше:
.
Отсюда следует, что точное число и соответствующее ему округленное число связаны равенством:
, где 
.
Число 
называется машинный эпсилон. Машинный эпсилон характеризует точность арифметики с плавающей запятой.
Машинный эпсилон определяют как наименьшее число , такое, что 
.
Один из вариантов оценки числа на языке пакета Mathematica:
For[ep=1.,1.+ep>1.,ep=ep/2];2 ep
Исходное число ep =1. делится многократно пополам до тех пор, пока не будет нарушено условие 
На печать выводится удвоенный результат последнего деления 
.
Отметим, что в библиотеках языка Си имеются встроенные значения машинного эпсилон для формата float: FLT_EPSILON=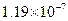 
и для формата double: DBL_EPSILON= 
.
