1. Свойства определителей. Миноры, алгебраические дополнения. Теорема Лапласа.
2. Матрица. Виды матриц. Действия над матрицами. Обратная матрица.
3. Решение СЛУ по формулам Крамера, методом Гаусса и обратной матрицы.
4. Прямая линия: общие уравнения. Через точку по данному уравнению. Через две точки. В отрезках.
5. Взаимное расположение прямых. Понятие о линиях 2-го порядка: окружность, гипербола, парабола.
6. Операции над векторами. Скалярное произведение векторов.
7. Применение векторов в аналитической геометрии.
8. Теоремы о пределах. Бесконечно малые и бесконечно большие величины
9. Замечательные пределы.
10. Понятие о непрерывности и разрывах функции.
11. Определение производной. Таблица производных.
12. Правило Лопиталя для вычисления пределов.
13. Возрастание и убывание функций. Экстремумы.
14. Выпуклости функций и точки перегиба.
15. Асимптоты: вертикальные, горизонтальные, наклонные.
16. Свойства неопределенного интеграла. Таблица интегралов.
17. Интегрирование по частям.
18. Определенный интеграл. Формуле Ньютона – Лейбница.
19. Свойства и геометрический смысл определенного интеграла.
20. Ряды. Сходимость и ее признаки.
21. Дифференциальные уравнения 1-го порядка. Уравнения 2-го порядка: однородные и неоднородные.
22. События. Основные определения. Виды случайных событий.
23. Классическое определение вероятности. Статистическое определение вероятности.
24. Выборки элементов. Размещения перестановки. Сочетания. Свойства сочетаний.
25. Теоремы сложения вероятностей для совместных и несовместных событий и следствия из них.
26. Условная вероятность. Зависимые и независимые события.
27. Теоремы умножения вероятностей для зависимых и независимых событий.
28. Формула полной вероятности. Формула Бейеса.
29. Повторные независимые испытания. Формула Бернулли.
30. Поток событий. Простейший поток событий. Формула Пуассона.
31. Локальная теорема Лапласа. Интегральная теорема Лапласа.
32. Понятие дискретной случайной величины. Числовые характеристики.
33. Непрерывная случайная величина. Интегральная функция распределения: её свойства, график. Вероятность попадания в заданный интервал.
34. Плотность распределения вероятностей. Определение, вероятностный смысл, свойства, график.
35. Числовые характеристики непрерывной случайной величины.
36. Равномерное распределение непрерывной случайной величины. Показательное распределение непрерывной случайной величины.
37. Нормальное распределение.
38. Общая задача линейного программирования. Основные теоремы. Многоугольник решений.
39. Этапы решения ЗЛП графическим методом (алгоритм решения).
40. Симплексный метод решения задачи линейного программирования. Постановка задачи. Математическая модель ЗЛП.
41. Алгоритм симплексного метода решения ЗЛП.
42. Двойственная задача к задаче планирования торговли. Алгоритм двойственного симплексного метода.
43. Целочисленное программирование. Общая формулировка задачи.
44. Графический метод решения задачи целочисленного программирования. Метод Гомори.
45. Общая постановка транспортной задачи. Алгоритм построения 1-го опорного плана.
46. Потенциалы. Алгоритм метода потенциалов.
47. Постановка задачи динамического программирования. Рекуррентные соотношения Беллмана (метод функциональных уравнений).
48. Математическая теория оптимального управления. Вариационные методы. Принцип максимума.
49. Графы и орграфы.
50. Основные понятия сетевой модели. Минимизация сети.
51. Формулировка задачи и характеристики СМО.
52. Функции полезности. Кривые безразличия. Функции спроса.
53. Уравнение Слуцкого. Кривые «доход-потребление» и «цены-потребление».
54. Коэффициенты эластичности. Модель Эрроу – Гурвица.
55. Модели межотраслевого баланса.
56. Общие модели развития экономики. Модель Солоу.
Тестовые задания
Задание 1
Вопрос 1. Что называется функцией?
1) число;
2) правило, по которому каждому значению аргумента х в соответствует одно и только одно значение функции у;
3) вектор;
4) матрица;
5) нет правильного ответа.
Вопрос 2. В каком случае можно определить обратную функцию?
1) когда каждый элемент имеет единственный прообраз;
2) когда функция постоянна;
3) когда функция не определена;
4) когда функция многозначна;
5) нет правильного ответа.
Вопрос 3. Какая функция называется ограниченной?
1) обратная;
2) функция f(x) называется ограниченной, если m≤f(x)≤M;
3) сложная;
4) функция f(x) называется ограниченной, если f(x)>0;
5) функция f(x) называется ограниченной, если f(x)≤0;
Вопрос 4. Какая точка называется предельной точкой множества А?
1) нулевая;
2) т.х0 называется предельной точкой множества А, если в любой окрестности точки х0 содержатся точки множества А, отличающиеся от х0;
3) не принадлежащая множеству А;
4) нет правильного ответа;
5) лежащая на границе множества.
Вопрос 5. Может ли существовать предел в точке в том случае, если односторонние пределы не равны?
1) да;
2) иногда;
3) нет;
4) всегда;
5) нет правильного ответа.
Задание 2
Вопрос 1. Является ли функция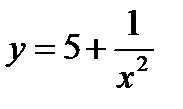 
бесконечно малой при х→∞?
1) да;
2) нет;
3) иногда;
4) всегда;
5) нет правильного ответа.
Вопрос 2. Является ли функция 
бесконечно большой при х→∞?
1) да;
2) нет;
3) иногда;
4) если х=0;
5) нет правильного ответа.
Вопрос 3. Является ли функция у=sin x бесконечно большой при х→∞?
1) да;
2) нет;
3) иногда;
4) всегда;
5) нет правильного ответа.
Вопрос 4. Является ли функция у=cos x бесконечно большой при х→∞?
1) да;
2) нет;
3) иногда;
4) всегда;
5) нет правильного ответа.
Вопрос 5. Является ли функция у=tg x бесконечно большой в т. х0=0?
1) да;
2) иногда;
3) всегда;
4) нет;
5) нет правильного ответа.
Задание 3
Вопрос 1. Является ли произведение бесконечно малой функции на функцию ограниченную, бесконечно малой функцией?
1) нет;
2) да;
3) иногда;
4) не всегда;
5) нет правильного ответа.
Вопрос 2. В каком случае бесконечно малые α (х) и β(х) называются бесконечно малыми одного порядка в точке х0?
1) если они равны;
2) если 
;
3) если 
;
4) если их пределы равны 0;
5) нет правильного ответа.
Вопрос 3. Сколько видов основных элементарных функций мы изучили?
1) 5;
2) 1;
3) 0;
4) 2;
5) 3.
Вопрос 4. Чему равен предел константы С?
1) 0;
2) е;
3) 1;
4) ∞;
5) с.
Вопрос 5. Является ли степенная функция непрерывной при любом положительном значении показателя степени?
1) нет;
2) да;
3) иногда;
4) при х >1;
5) нет правильного ответа.
ЗАДАНИЯ ДЛЯ АКР
ВАРИАНТ 1
1. Решить систему уравнений:
2. Вычислить пределы: 1) 
; 2) 
; 3) 
;
3. Найти производные функций:
а) 
; б) 
; в) 
;
4. Решить интегралы:
1) 
2) 
3) 
4) 
5.
1. Герман из «Пиковой дамы» вынимает 3 карты из колоды в 52 листа. Найти вероятность того, что это будут: тройка, семерка, туз.
2. Из букв разрезной азбуки составлено слово «ананас». Ребенок, не умеющий читать, смешал буквы и разложил их вновь в произвольном порядке. Найти вероятность того, что снова получится слово «ананас».
3. Предположим, что 5% всех мужчин и 0,25% всех женщин дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это: а) мужчина; б) женщина (считать, что их поровну).
4. В среднем пятая часть поступающих в продажу автомобилей некомплектны. Найти вероятность того, что среди десяти автомобилей имеют некомплектность: а) три автомобиля; б) менее трех.
5. Вероятность того, что саженец елки прижился, равна 0,8. посажено 400 елочных саженца. Какова вероятность того, что вырастет а) 200 деревьев; б) не менее 250 деревьев.
6. Решить ЗЛП
а) графическим методом 
б) симплексным методом 
ВАРИАНТ 2
1. Решить систему уравнений: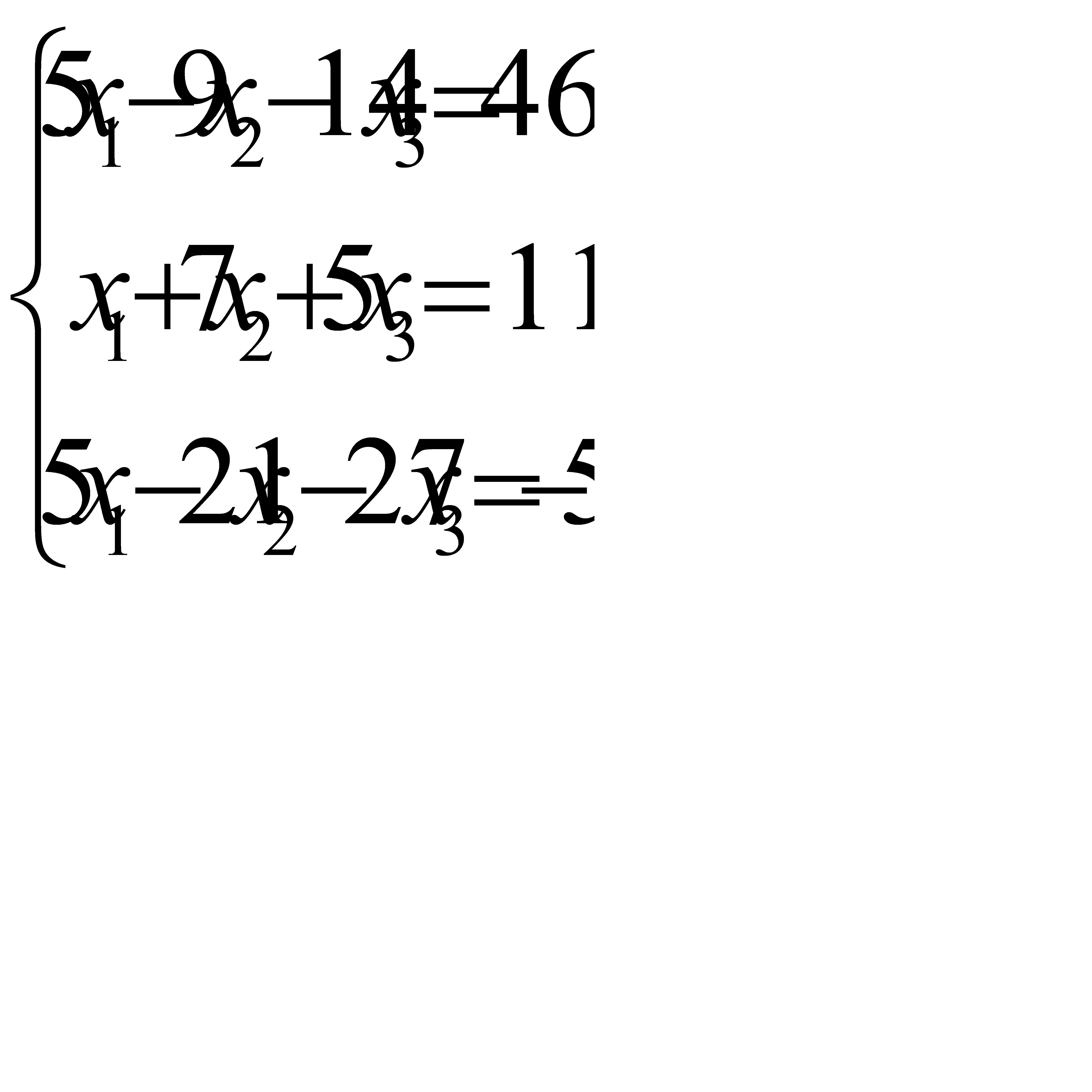 
2. Вычислить пределы: 1) 
; 2) 
;3) 
;
3. Найти производные функций:
а) 
; б) 
; в) 
;
4. Решить интегралы: 1) 
2) 
3) 
4) 
5.
1. В ящике лежат 15 красных, 9 синих и 6 зеленых шаров, одинаковых на ощупь. Наудачу вынимают 6 шаров. Какова вероятность того, что вынуты 1 зеленый, 2 синих и 3 красных шара.
2. Абонент забыл две последние цифры номера и набрал из наудачу, помня только, что эти числа нечетные и разные. Найти вероятность того, что номер набран правильно.
3. Два консервных завода поставляют в магазин мясные и овощные консервы, причем первый поставляет в три раза большего второго. Доля овощных консервов в продукции первого завода составляет 60%, а второго – 50%. Для контроля в магазине наудачу взято одно изделие. Какова вероятность того, что это мясные консервы?
4. Отдел технического контроля проверяет изделие на стандартность. Вероятность того, что изделие стандартно, равна 0,8. Найти вероятность того, что из двух проверенных изделий только одно стандартно.
6. Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженых семян число проросших будет а) 800 б) заключаться между 790 и 830.
7. Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения числа возвращенных в срок кредитов из 5 выданных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
6. Решить ЗЛП
а) графическим методом 
,
б) симплексным методом 
ВАРИАНТ 3
1. Решить систему уравнений: 
2. Вычислить пределы: 1) 
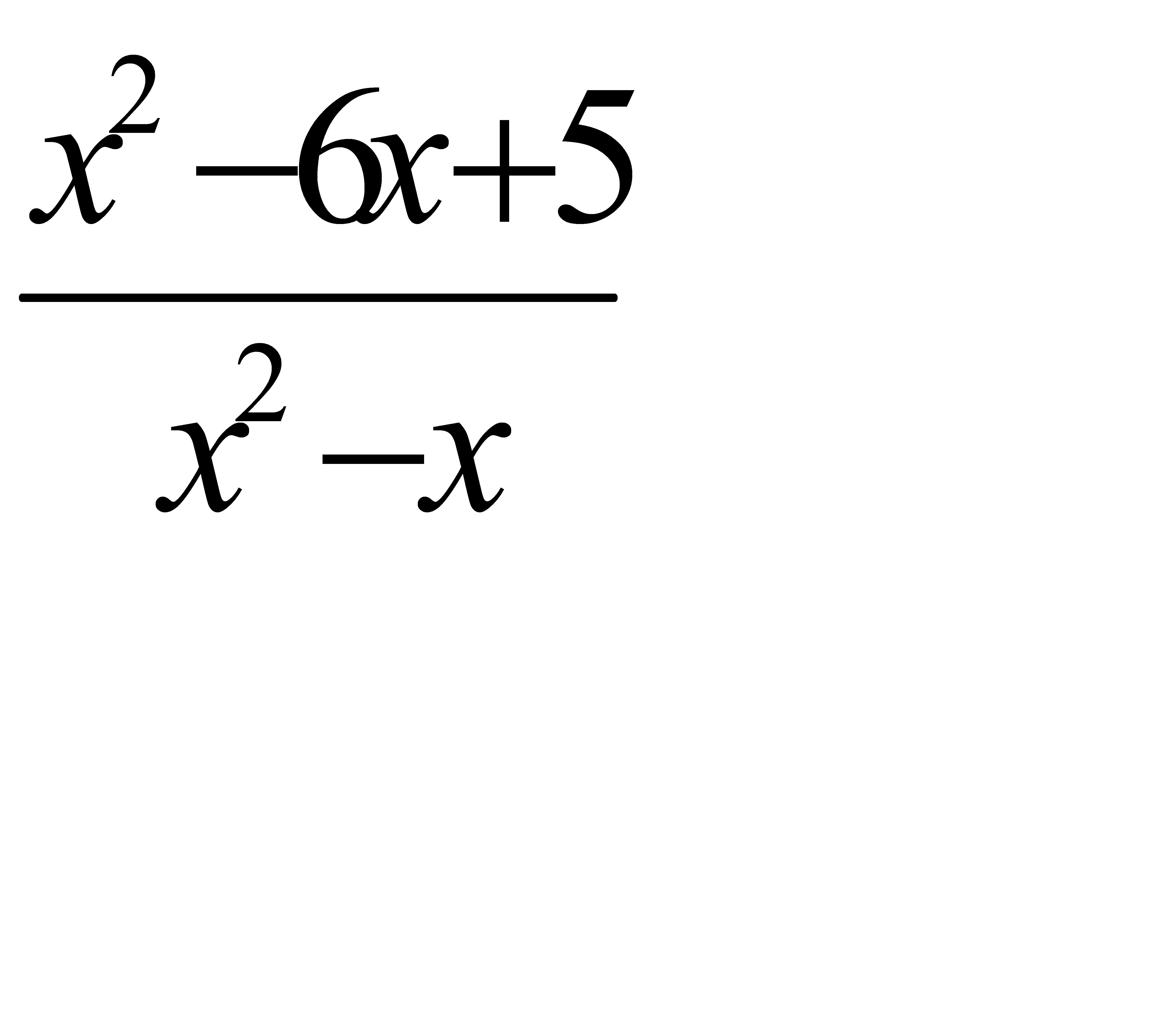; 2) 
; 3) 
3. Найти производные функций: а) 
;б)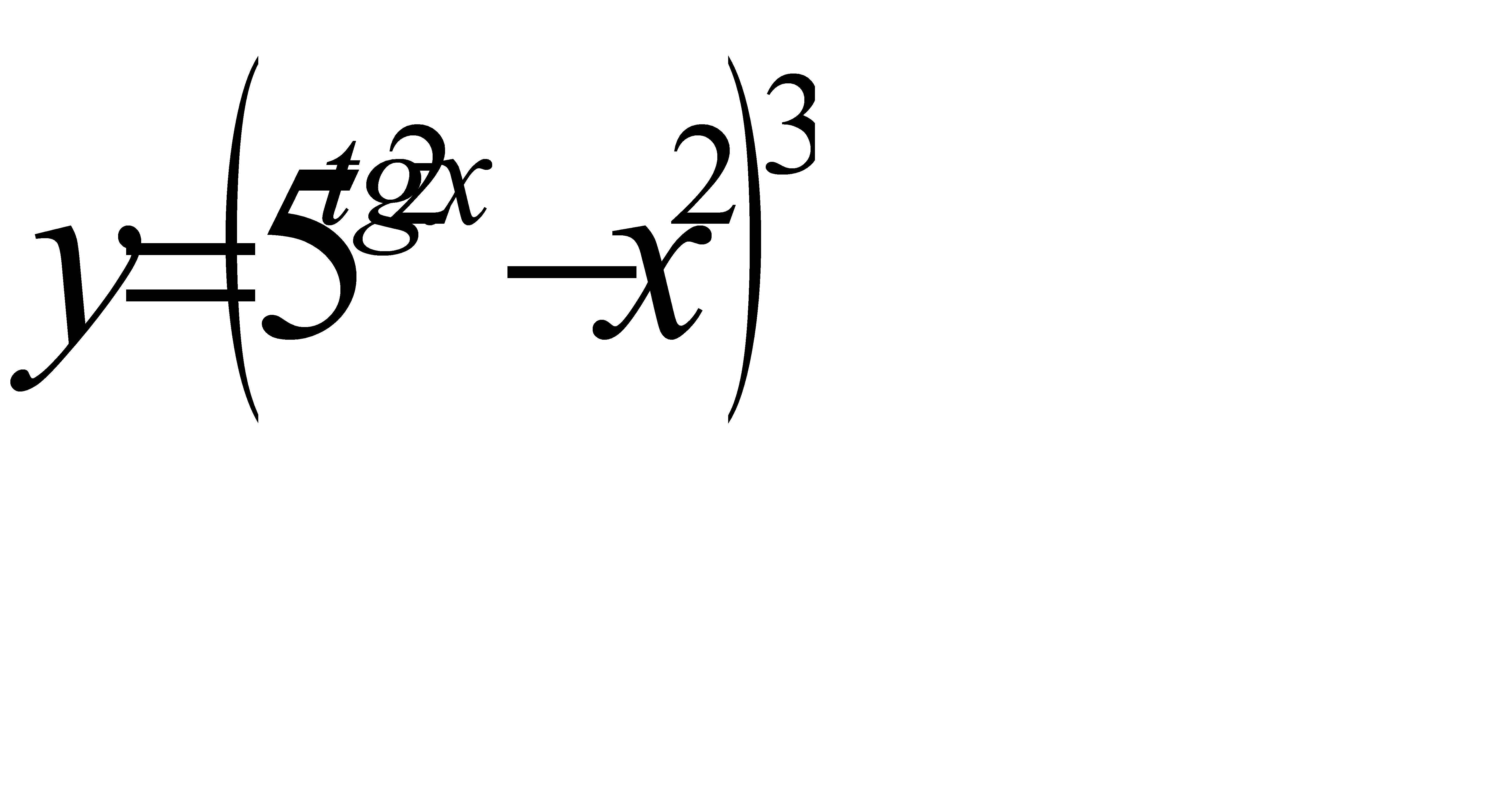 
;
в) 
;
4. Решить интегралы, результат проверить дифференцированием:
1) 
2) 
3) 
4) 
5.
1. Владелец одной карточки лотереи «Спортлото» (6 из 49) зачеркивает 6 номеров. Какова вероятность того, что им будет угадано 5 номеров в очередном тираже?
2. В лифт семиэтажного дома вошло три человека. Каждый из них с одинаковой вероятностью выходит на любом этаже, начиная со второго. Найти вероятность, что все пассажиры выйдут на четвертом этаже.
3. На склад от трех поставщиков поступило 200, 300 и 500 изделий соответственно. Продукция первого поставщика имеет 5% брака, второго – 6%, третьего – 4%. Найти вероятность получения со склада годного изделия.
4. В квартире 4 электролампочки. Для каждой лампочки вероятность не перегореть в течение года равна 5/6. Какова вероятность того, что в течение года придется заменить не менее 3 лампочек.
5. Вероятность появления стандартной продукции в каждой из независимых выборок, проводимых товароведом, равна 0,8. Найти вероятность того, что стандартная продукция появится а) 120 раз в 144 выборках; б) более половины.
6. Р ешить ЗЛП
а) графическим методом 
б) симплексным методом 
