МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКОЙ РАБОТЫ № 2
Тема: «Действия над степенями с рациональным и действительным показателем».
Цель занятия: Обобщить и систематизировать знания по теме «Свойства корней и степеней»; закрепить умения использовать полученные знания для преобразования алгебраических выражений.
Контрольные вопросы.
1. Определение корня натуральной степени из числа.
2. Основные свойства корня натуральной степени из числа.
3. Определение степени с рациональным показателем.
4. Основные свойства степени с рациональным показателем.
5. Понятие степени с действительным показателем.
6. Основные свойства степени с действительным показателем.
7. Как избавиться от иррациональности в знаменателе.
Примеры и последовательность выполнения заданий
Пример 1. Вычислить
а) 
б ) 
в) 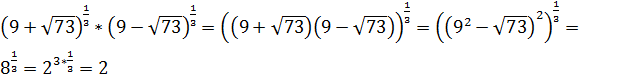
г) 
д) 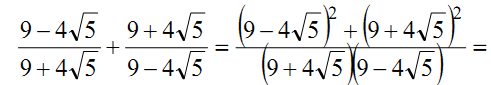

Пример 2. Упростить выражение и найти его значение
а)  при а = 5
при а = 5
Решение
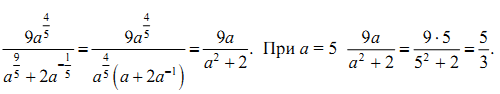
б)  при b=2, c=5
при b=2, c=5
Решение

Пример 3. Избавиться от иррациональности в знаменателе
а) 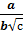 Решение
Решение 
б) 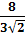 Решение
Решение 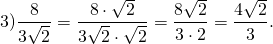
в)  Решение
Решение  .
.
г)  Решение:
Решение: 
д) 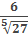 Решение:
Решение: 
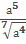 Решение:
Решение: 
Выполните следующие задания
1 вариант
Задание 1. Вычислить
а)  .
.
б)  ;
;
в)  ;
;
г)  );
);
д)  .
.
Задание 2. Упростить выражение и найти его значение
а) 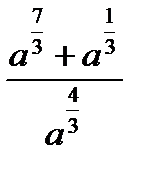 при а = 2
при а = 2
б)  при а=7, с=3
при а=7, с=3
Задание 3. Избавиться от иррациональности в знаменателе
а) 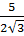 ; б)
; б) 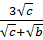 ;в)
;в)  ;
;
г)  д)
д) 
2 вариант
Задание 1. Вычислить
а) 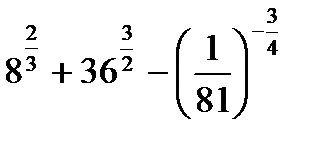 .
.
б)  ;
;
в) 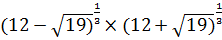 ;
;
г)  );
);
д) 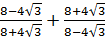 .
.
Задание 2. Упростить выражение и найти его значение
а) 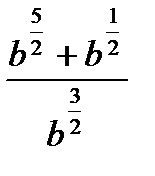 при b=3
при b=3
б)  при а=9, с=2
при а=9, с=2
Задание 3. Избавиться от иррациональности в знаменателе
а)  ; б)
; б)  ; в)
; в)  ;
;
г) 
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКОЙ РАБОТЫ № 4
Учебная дисциплина: Математика
Тема: «Преобразования логарифмических выражений. Решение упражнений».
Цель занятия: Обеспечить закрепление понятия логарифм числа; формирование практических навыков преобразования логарифмических выражений на основе изученного теоретического материала (определения и свойств логарифмов).
Контрольные вопросы.
1. Понятие логарифма числа.
2. Основное логарифмическое тождество.
3. Понятие десятичного логарифма числа.
4. Понятие натурального логарифма числа.
5. Основные свойства логарифмов.
6. Формула перехода от логарифма по одному основанию к логарифму по другому основанию.
Примеры и последовательность выполнения заданий.
Пример 1. Вычислить. 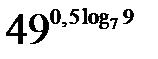
Решение. 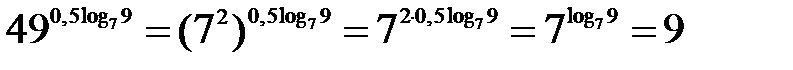
Пример 2. Вычислить.
а) 
Решение. 
б) 
Решение.  Пример 3. Упростить выражение.
Пример 3. Упростить выражение. 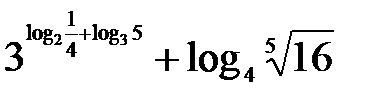
Решение. 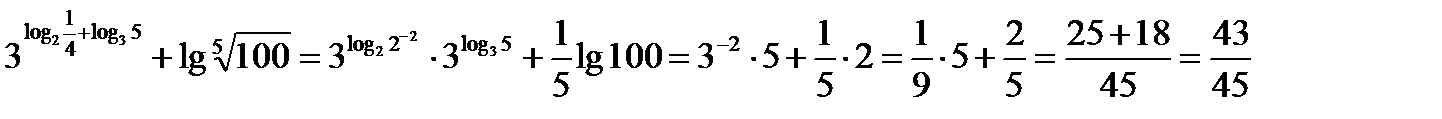
Пример 4. Вычислить. 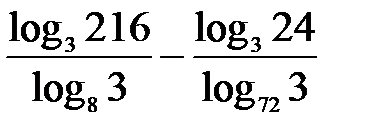
Решение. 

Выполните следующие задания
1 вариант2 вариант
Вычислить:
1) 
2) 
3) 
4) 
5) 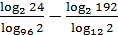
6) 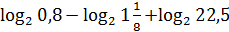
7) 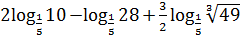
8)  (*)
(*)
1) 
2) 
3) 
4) 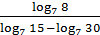
5) 
6) 
7) 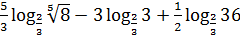
8) 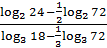 (*)
(*)
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКОЙ РАБОТЫ № 5
Учебная дисциплина: Математика
Тема: ««Логарифмические уравнения, и методы их решения»».
Цель занятия: Обобщение свойств логарифмов, применение их к решению уравнений;
Закрепление основных методов решения логарифмических уравнений
Контрольные вопросы.
1. Что понимают под логарифмическим уравнением?
2. Что называется корнем уравнения?
3. Что значит «решить уравнение»?
4. Какие уравнения называются равносильными?
5. Что такое потенцирование?
6. Обязательной ли является в общем случае проверка найденных значений неизвестного по условию уравнения?
7. Какие свойства логарифмов вам известны?
Примеры и последовательность выполнения заданий.
1. Простейшее логарифмическое уравнение:
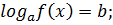
ОДЗ: 
Решение:
1)  ;
;
2) Отбор корней, удовлетворяющих ОДЗ.
Пример:

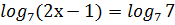
2х-1=7  2х=8
2х=8  х=4
х=4
Проверка:  =1
=1
1=1
Ответ: х=4.






