Методы эффективного кодирования некоррелированной последовательности знаков, код Шеннона-Фано

Введение

Важнейшей частью информатики как науки является теория информации, которая занимается изучением информации как таковой, ее появлением, развитием и уничтожением. К этой науке близко примыкает теория кодирования, в задачу которой входит изучение форм представления информации при ее передаче по различным каналам связи, а также при хранении и обработке.

Кодирование в широком смысле – преобразование сообщений в сигнал. Кодирование в узком смысле – представление дискретных сообщений определенными сочетаниями символов.

Кодирование осуществляется, с одной стороны, для того, чтобы обеспечить наилучшее согласование характеристик источника сообщений и канала, с другой стороны, для повышения достоверности передачи информации при наличии помех. Кроме того, при выборе системы кодирования стремятся обеспечить простоту и надежность аппаратной реализации устройств.

В процессе кодирования сообщений длинная последовательность обычно формируется из кодовых комбинаций, каждая из которых соответствует одному знаку. Число символов, из которых составлена такая кодовая комбинация, называется значностью или длиной кода. Количество разных символов, использованных для построения кодовой комбинации, называется основанием кода. Физически символы реализуются ввидеосигналов, несущих некоторые признаки.

С точки зрения экономии времени передачи сообщений, выгодно иметь меньше цифр в представлении числа. Однако увеличениес целью уменьшения приводит к усложнению устройств, реализующих m признаков (устойчивых состояний).. Можно показать, что по этому критерию наиболее эффективной является троичная система. Тем не менее, наиболее широко используются незначительно уступающие троичной системе двоичные коды.

Цель курсовой работы - изучение основные методы эффективного кодирования, программно реализовать один из методов.

Для достижения поставленной цели предполагается решение следующих задач:

· изучить методы эффективного кодирования;

· обозначить достоинства и недостатки методов;

· детально разобрать метод, выбранный для реализации;

· выбрать язык программирования, на котором будет реализован данный метод;

· провести тестирование программы.

Объектом курсовой работы является изучение методов эффективного кодирования. Более подробно будет рассмотрен методика кодирования Хаффмана, что является её предметом.

Объект

Предмет

Цель

Задачи

Методы эффективного кодирования

Методы эффективного кодирования некоррелированной последовательности знаков, код Шеннона-Фано

Теорема Шеннона отвечает на вопрос, при каких условиях возможно впринципе построение кода, обеспечивающего передачу всех сообщений, формируемых источником. Естественно стремление строить наилучшие, с точки зрения максимума передаваемой информации, коды. Для того чтобы каждый символ (кода нес максимум информации, символы кодовой комбинации должны быть независимы и принимать значения (0 и 1) с равными вероятностями. Построение эффективных кодов в случае статистической независимости символов сообщений опирается на методики Шеннона и Фано (код Шеннона-Фано).

Код строится следующим образом. Кодируемые знаки выписывают в таблицу в порядке убывания их вероятностей в сообщениях. Затем их разделяют на две группы так, чтобы значения сумм вероятностей в каждой группе были близкими. Все знаки одной из групп в соответствующем разряде кодируются, например, единицей, тогда знаки второй группы кодируются нулем. Каждую

полученную в процессе деления группу подвергают вышеописанной операции до тех пор, пока в результате очередного деления в каждой группе не останется по одному знаку (Таблица 1).

В приведенном примере среднее число символов на один знак 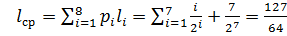, где 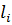– число символов в i -м разряде, имеет такую же величину, как и энтропия, рассчитанная в среднем на один знак (Формула 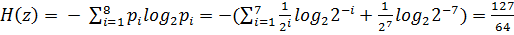1):

(1)

 

Таблица 1 ─ Код Шеннона-Фано по одному знаку

Знаки	Вероятности	Коды
Z1	1/2
Z2	1/4
Z3	1/8
Z4	1/16
Z5	1/32
Z6	1/64
Z7	1/128
Z8	1/128

Совпадение результатов связано с тем, что вероятности знаков являются целочисленными отрицательными степенями двойки.

В общем случае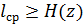

Если величина среднего числа символов на знак оказывается значительно большей, чем энтропия, то это говорит об избыточности кода. Эту избыточность можно устранить, если перейти к кодированию блоками. Рассмотрим простой пример кодирования двумя знаками z₁,z₂ с вероятностями их появления в сообщениях 0,1 и 0,9 соответственно.

Еслиодин из этих знаков кодировать, например, нулем, а другой единицей, по одному символу на знак, имеем соответственно

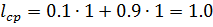
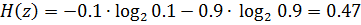
При переходе к кодированию блоками по два знака (Таблица 2)эффект достигается за счет того, что при укрупнении блоков, группы можно делить на более близкие по значениям суммарных вероятностей подгруппы 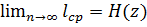, где n– число символов в блоке.

Таблица 2 ─ Код Шеннона-Фано по блокам

Знаки	Вероятности	Коды
Z1Z1	0,81
Z2Z1	0,09
Z1 Z2	0,09
Z2Z2	0,01

Методика Шеннона-Фано не всегда приводит к однозначному построению кода, вследствиеотсутствия рамок деления множество кодируемых знаков на подгруппы. Кроме того, методика не обеспечивает отыскания оптимального множества кодовых слов для кодирования данного множества сообщений. Под оптимальностью подразумевается то.что никакое другое однозначно декодируемое множество кодовых слов не имеет меньшую среднюю длину кодового слова, чем заданное множество.