РАБОТА ЦИКЛА ГТД
Физический смысл работы цикла. В термодинамике работой цикла (строго говоря, удельной работой цикла) называют полезно используемое тепло, т.е. разность между теплом, подведенным к 1 кг рабочего тела и отведенным от него. На основании (5.4) можно записать
Le = Q1 – Q2 = Lр – Lсж. (5.5)
Выражая Lр и Lсж через кинетическую энергию потока и работу узлов согласно (5.3) и (5.2), получаем
L e = – + LтII, (5.6)
где LтII = Lт – Lк – избыточная работа турбины.
В ТРДД избыточная работа турбины передается в наружный (второй – II) контур, а в ТВД – на винт. В ТРД механическая работа от двигателя не отводится (L тII = 0), и полезное тепло, численно равное работе цикла, идет целиком на приращение кинетической энергии рабочего тела.
В общем случае работа цикла ГТД складывается из приращения кинетической энергии рабочего тела, проходящего через основной контур двигателя, и механической работы L тII.
Таким образом, работой цикла называют и полезно используемое тепло (5.5), и механическую энергию (5.6). На основании (5.5) определяется величина работы цикла, а на основании (5.6), как показано в гл. 6, определяется в конечном счете скорость истечения газа из двигателя, а следовательно и его тяга.
Необходимо подчеркнуть, что для ТРДД все величины, входящие в уравнение (5.6), отнесены к 1 кг рабочего тела, проходящего через основной (внутренний) контур двигателя.
Вывод формулы работы цикла, выраженной через параметры цикла. Выразим работу цикла через параметры рабочего процесса, для чего действительные работы расширения Lр и сжатия Lсж в формуле (5.5) выразим через их идеальные значения (см. рис. 5.1), чтобы затем от отношения температур по уравнению изоэнтропы перейти к отношению давлений.
Отношение работ сжатия в идеальном и действительном процессах называют суммарным КПД процесса сжатия [31]:
h сж = Lсж s /Lсж. Он показывает, какую долю от величины Lсж составляет идеальная работа, затраченная на сжатие воздуха без потерь при одинаковой степени повышения давления в обоих случаях, и оценивает потери в процессе сжатия воздуха в воздухозаборнике и компрессоре. Для дозвуковых и небольших сверхзвуковых скоростей полета h сж = 0,75... 0,85.
Отношение действительной работы расширения к ее значению в идеальном процессе называют суммарным КПД расширения: h р = Lр /Lр s. С его помощью учитываются потери в камере сгорания, турбине и в канале сопла. Величина КПД h р изменяется обычно в пределах h р = 0,85... 0,95.
Выражая действительную работу, затраченную на сжатие и расширение, через идеальную, а идеальную – через температуру начала и конца процесса и подставляя эти выражения в уравнение (5.5), имеем
L e = c р г (T *г – Тсs) h р – c р (T *к s – T н).
Если вынести T *г и Tн за скобки, то с учетом уравнения изоэнтропы получим [31]
L e = c р г T *г h р – c p T н. (5.7)
Здесь p S = p *к / p н – суммарная степень повышения (понижения) давления в цикле, равная произведению степеней повышения давления во входном устройстве и компрессоре:
p S = p V s вх p *кS. (5.8)
Из полученного уравнения видно, что работа цикла зависит от величин T *г, p S, которые называются параметрами рабочего процесса (их называют также параметрами цикла), КПД процессов сжатия h сж и расширения h р, а также от температуры наружного воздуха T н. Она не зависит от давления наружного воздуха. С изменением скорости полета изменяется степень повышения давления p V и, следовательно, p S. Поэтому работа цикла зависит от скорости полета.
При одинаковых параметрах цикла, постоянной температуре наружного воздуха и одинаковых КПД (для трех основных типов ГТД) работа цикла этих двигателей одинаковая:
L e ТРД = L e ТРДД = L e ТВД.
ЗАВИСИМОСТЬ РАБОТЫ ЦИКЛА ОТ ЕГО ПАРАМЕТРОВ
Проанализируем зависимость работы цикла сначала от температуры газа перед турбиной, а затем от суммарной степени повышения давления при условии, что T н, h сж и h р постоянны.
5.3.1. Зависимость работы цикла от температуры газа
перед турбиной
Пусть температура газа перед турбиной изменяется при p S = const. Из уравнения (5.7) следует, что с увеличением температуры T *г работа расширения газа увеличивается пропорционально этой температуре, а работа сжатия от нее не зависит. Поэтому работа цикла изменяется по T *г линейно (рис. 5.3).
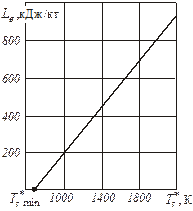Рис. 5.3. Зависимость работы цикла L eот T *г при p S = 25,
T н = 216 К, h сж = 0,85, h р= 0,93
|
При снижении T *г работа цикла уменьшается и при некоторой минимальной температуре T *г min обращается в нуль. Используя уравнение (5.7), из условия L e = 0 получаем выражение для T *г min:
T *г min= T н =.
(5.9)
Для идеального цикла (при отсутствии гидравлических потерь в процессах сжатия и расширения h сж= h р= 1) T *г min= T *к s. Следовательно, работа цикла равна нулю, когда температура газа перед турбиной равна температуре воздушного потока за компрессором и тепло к рабочему телу не подводится (Q1 min= 0).
Для действительного цикла минимальная температура газа перед турбиной выше температуры воздуха за компрессором, следовательно, тепло к рабочему телу подводится, т.е. Q1 min > 0. Так как работа цикла при этом равна нулю, все подведенное тепло идет на преодоление гидравлических потерь и отводится от двигателя с выхлопными газами.
Из (5.9) следует, что T *г min зависит от суммарной степени повышения давления p S, величины T н и от потерь в цикле (рис. 5 4).
Рис. 5.4. Зависимости T *г min от p S при различных значениях T н:
- - - – h сж = 0,75, h р = 0,83; – h сж = 0,85, h р = 0,93
5.3.2. Зависимость работы цикла от суммарной степени
повышения давления
Рассмотрим зависимость работы цикла от суммарной степени повышения давления при условии, что другие параметры, от которых зависит величина L e, неизменны. Для этого представим уравнение (5.7) в виде
L e = c p T н h р. (5.7а)
Из (5.7а) следует, что работа цикла равна нулю в двух случаях: при p S = 1 и при
p S = = p S пр. (5.9а)
В первом случае давление в камере сгорания равно атмосферному, отсутствует перепад давления при расширении газа и рабочее тело неработоспособно, хотя тепло к газу подводится.
Во втором случае работоспособность газа высокая (большой перепад давления в процессе расширения), но подведенного тепла хватает только на преодоление потерь. Это объясняется тем, что суммарная степень повышения давления достигает предельного значения p S пр, при котором заданная температура становится минимальной T *г = T *г min, цикл вырождается. Это очевидно, если из уравнения (5.9а) выразить T *г через p S пр. Так как работа цикла обращается в нуль при двух значениях p S (рис. 5.5), а величина L e всегда положительна, то она должна иметь максимум. Для определения максимума функции L e = f (p S) и соответствующего оптимального значения p S opt представим уравнение (5.7) в следующем виде:
Рис. 5.5. Зависимости работы цикла и определяющих ее параметров от p S при T н = 216 К
|
L e = c p T *г h р – c p T н (e – 1),
где e=.
Если найти производную
= –
и приравнять ее нулю, то получим
e opt =,
откуда
p S opt = =. (5.10)
Оптимальная степень повышения давления, как и величина p S пр, является функцией степени повышения температуры рабочего тела T *г /T н и потерь в цикле. Чем больше подведено тепла и меньше потери, тем больше величина p S opt.
Рис. 5.6. Зависимость оптимальной степени повышения давления в компрессоре от числа M п при T *г / T н = var
|
Оптимальная степень повышения давления p S opt не зависит от скорости полета. Величине p S opt, согласно (5.8), соответствует оптимальная степень повышения давления компрессора p *к opt = p S opt / p V sвх, которая зависит от скорости полета: с увеличением V п степень повышения давления в воздухозаборнике p V sвх повышается, а p *к opt снижается. Она снижается практически до единицы при скоростях полета, соответствующих числам M п = 2,5... 3 (рис. 5.6).
Итак, с увеличением pS работа цикла сначала возрастает, достигая максимума, а затем снижается. Возникновение максимума работы цикла объясняется противоположным влиянием двух факторов: ростом работоспособности рабочего тела (ростом избыточного давления в камере сгорания, что приводит к уменьшению потерь тепла Q 2) и одновременным снижением количества подведенного тепла Q 1 вследствие повышения температуры воздуха за компрессором (см. рис. 5.5). Вначале, при малых значениях p S, преобладает влияние первого фактора, а затем – второго.
Заметим, что снижение работы цикла до нуля при T *г = T *г min (см. рис. 5.3) и при p S = p S пр (см. рис. 5.5) имеет одинаковый физический смысл. В обоих случаях цикл вырождается вследствие уменьшения количества тепла, подведенного к рабочему телу. В первом случае теплоотвод уменьшается из-за снижения температуры газа перед турбиной, а во втором – из-за увеличения температуры воздуха на выходе из компрессора.
Рис. 5.8. Зависимость работы цикла L e от p S при T *г = var, T н = 216 К
|
Проведенный анализ показывает, что для значительного увеличения работы цикла необходимо изменять не только температуру газа перед турбиной, но и суммарную степень повышения давления. Например, с увеличением температуры T *г от 1000 до 2000 К оптимальная степень повышения давления p S opt увеличивается от 10 до 40, а работа цикла – от 210 до 830 кДж/кг, т.е. в 4 раза (рис. 5.8).
ЭФФЕКТИВНЫЙ КПД
Эффективным КПД газотурбинного двигателя называют отношение работы цикла L e к располагаемой энергии внесенного в двигатель топлива Q 0:
h е = L e / Q0.
Он показывает, какая часть располагаемой энергии топлива преобразуется в полезную работу и, следовательно, характеризует двигатель как тепловую машину.
Располагаемая энергия внесенного в двигатель топлива Q0, приходящегося на 1 кг воздуха, связана с теплом Q1, подведенным к 1 кг воздуха, через коэффициент полноты сгорания топлива. Согласно (4.3) Q0 = Q1 / h г, и поэтому
h е = h г. (5.11)
Умножим числитель и знаменатель полученной формулы на L e s (работа идеального цикла) и, пренебрегая различием Q 1 и Q1 s (тепло, подведенное в действительном и идеальном циклах), представим (5.11) в приближенном виде:
h е» h г h th r I, (5.12)
где h t = L e s / Q 1 s – термический КПД идеального цикла; h r I = L e / L e s – коэффициент гидравлических потерь в основном контуре двигателя.
Термический КПД показывает, какую часть от подведенного тепла составляет работа идеального цикла. Он учитывает потери тепла Q 2 s, обусловленные несовершенством идеального цикла Брайтона (p= const).
Если в формулу h t = 1 – Q 2 s / Q 1 s подставить Q 1 s и Q 2 s, выраженные через параметры цикла,
Q 1 s = c p; Q 2 s = c p,
то получим
Рис. 5.9. К сравнению циклов ГТД при
одинаковых T *г, p S и T н:
 - - - – идеального; – действительного
|
h t = 1 –. (5.13)
Из (5.13) видно, что термический КПД однозначно определяется суммарной степенью повышения давления в цикле.
Коэффициент гидравлических потерь h r I показывает, какую часть от идеальной работы цикла составляет его эффективная (действительная) работа. Он учитывает работу, затраченную на преодоление гидравлических и газодинамических потерь в процессах сжатия, подвода тепла и расширения, L r I = L r сж + L r р:
h r I = 1 –. (5.14)
Как следует из (5.11), эффективный КПД зависит от тех же параметров, от которых зависит работа цикла, и, кроме того, от коэффициента полноты сгорания топлива.
При одинаковых параметрах рабочего процесса и одинаковом уровне потерь три основных типа ГТД не отличаются друг от друга по величине работы цикла и подведенного тепла. Следовательно, они не отличаются и по эффективному КПД:
h eТРД = h e ТРДД = h e ТВД.
5.5. ЗАВИСИМОСТЬ ЭФФЕКТИВНОГО КПД
ОТ ПАРАМЕТРОВ ЦИКЛА
Проанализируем зависимость h e, как и Le, сначала от T *г, затем от p S при постоянных значениях T н, h сж, h р и, кроме того, при h г = const.
Рис. 5.10. Зависимости коэффициента гидравлических потерь и эффективного КПД от T *г
(p S = 25, T н =216 К)
|
Зависимость эффективного КПД от температуры газа перед турбиной. Рассмотрим ее при p S= const.
Если T *г = T *г min, то работа цикла равна нулю, а Q1 больше нуля. Следовательно, согласно уравнению (5.11), эффективный КПД также равен нулю. В этом случае все подведенное тепло идет на преодоление потерь.
С ростом T *г увеличивается работа цикла, что приводит к повышению коэффициента гидравлических потерь h r I (см. формулу (5.14), в которой величину L rI с некоторыми допущениями можно принять постоянной) и, следовательно, эффективного КПД.
Если T *г стремится к бесконечности, то h r I стремится к пределу, равному, строго говоря, КПД процесса расширения, а h e к произведению трех величин: термического КПД, КПД процесса расширения и коэффициента полноты сгорания топлива (рис. 5.10).
Зависимость эффективного КПД от суммарной степени повышения давления. Проанализируем эту зависимость при условии, что все остальные величины, от которых зависит h e, постоянны.
Рис. 5.11. Зависимости термического КПД, коэффициента гидравлических потерь и эффективного КПД от p S (T *г = 1600 К, Т н = 216 К)
|
При p S = 1 и p S = p S пр эффективный КПД равен нулю, так как работа цикла равна нулю, а подведенное тепло Q 1 > 0. Следовательно, в диапазоне значений p S от 1 до p S пр КПД должен иметь максимум.
В указанном диапазоне эффективный КПД изменяется в соответствии с изменением произведения h t h r I. С увеличением суммарной степени повышения давления термический КПД монотонно увеличивается (рис. 5.11). Коэффициент гидравлических потерь изменяется так же, как и работа идеального цикла, что следует из анализа формулы (5.14) при L r I = const, и имеет максимум при соответствующей оптимальной степени повышения давления p S opt.
С повышением p S от 1 до p S opt эффективный КПД увеличивается, так как увеличиваются термический КПД и коэффициент гидравлических потерь. В диапазоне значений p S, близких к p S орt, эффективный КПД продолжает расти вследствие повышения термического КПД, при этом величина h r I сохраняется примерно постоянной. Максимума он достигает при условии
= –.
Таким образом, степень повышения давления p 'S, при которой эффективный КПД становится максимальным, больше величины p S opt. При дальнейшем повышении p S в диапазоне от p 'S до p S пр КПД h e снижается из-за уменьшения коэффициента гидравлических потерь.
Наличие максимума эффективного КПД объясняется противоположным влиянием двух факторов: ростом работоспособности рабочего тела с увеличением p S (ростом термического КПД) и уменьшением коэффициента гидравлических потерь вследствие снижения количества подведенного тепла при высоких значениях суммарной степени повышения давления. В конечном счете возникновение максимума эффективного КПД объясняется влиянием факторов, которые обусловливают максимум работы цикла.
Величина p 'S, как и p S opt, зависит от степени повышения температуры T *г / T н и от потерь в цикле. С увеличением температуры газа перед турбиной от 1000 до 2000 К величина p 'S увеличивается от 20 до 150 при принятом уровне потерь (рис. 5.12), что в 2 – 4 раза превышает оптимальную степень повышения давления p S opt. В результате максимальный эффективный КПД увеличивается от ~ 0,33 до ~ 0,53.
Рис. 5.12. Зависимости эффективного КПД от p S при различных T *г (Tн = 216 К, h сж = 0,86, h р = 0,94 и h г = 0,99)
|
Зависимости эффективного КПД и работы цикла от суммарной степени повышения давления и температуры газа перед турбиной ограничены предельной степенью повышения давления и, кроме того, максимальной температурой T *г max, соответствующей стехиометрическому сгоранию топлива (штриховые линии на рис. 5.8 и 5.12). Штриховые линии соответствуют максимально возможному теплоподводу и, следовательно, предельным возможностям воздушно-реактивного двигателя, работающего по циклу с подводом тепла при p = const и с использованием керосина в качестве топлива.
Резюме
(по теме "Газотурбинный двигатель как тепловая машина")
1. Газотурбинный двигатель как тепловая машина характеризуется работой цикла и эффективным КПД, которые зависят от следующих параметров: T *г, p S, T н, h сж, h р, h г.
2. Повышение температуры T *г приводит к монотонному увеличению работы цикла, что объясняется увеличением количества подведенного к рабочему телу тепла. Одновременно увеличивается эффективный КПД вследствие уменьшения доли гидравлических потерь от тепла, внесенного в двигатель с топливом.
3. Работа цикла и эффективный КПД имеют максимум по суммарной степени повышения давления, что объясняется противоположным влиянием двух факторов: ростом термического КПД с увеличением p S и одновременным уменьшением количества подведенного тепла.
4. Оптимальная степень повышения давления p S opt, соответствующая максимуму работы цикла, и степень повышения давления p 'S, соответствующая максимуму эффективного КПД, зависят от степени повышения температуры в цикле T *г / T н (т.е. главным образом от температуры газа перед турбиной) и величины гидравлических потерь. При увеличении T *г / T н и снижении потерь p S opt и p 'S увеличиваются; p 'S в 2 – 4 раза превышает p S opt. Оптимальная степень повышения давления компрессора p *к opt и соответственно p *к 'зависят, кроме того, от скорости полета, уменьшаясь с ее увеличением.
5. Для значительного увеличения работы цикла и эффективного КПД необходимо одновременно увеличивать температуру газа перед турбиной и суммарную степень повышения давления. Температурам T *г = 1500... 1700 К и степеням повышения давления в компрессоре p *к = 30... 50 при современном уровне потерь в условиях высотного полета при дозвуковой скорости соответствуют работа цикла L e» 500... 600 кДж/кг и эффективный КПД h e около 0,5.
6. Три основных типа ГТД (ТРД, ТРДД и ТВ(B)Д (ТВаД)) при одинаковых параметрах рабочего процесса как тепловые машины не отличаются друг от друга.
