Распределение нагрузок по панели, условия закрепления могут иметь различный вид. В предыдущих разделах были рассмотрены и приведены разрешающие уравнения равновесия для различных случаев нагружения панелей. Основываясь на полученных решениях, получим общий вариант граничных условий, который соответствует практически любым статическим и смешанным граничным условиям на поперечных краях панелей.
Естественные граничные условия поставленной задачи были получены в разд. 3.3 и представлены соотношениями (3.13) и (3.14) в виде
;
.
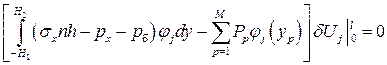Там же приведено описание всех обозначений.
Рассмотрим конкретное представление граничных условий, показанных на рис.3.1. Раскроем статические граничные условия, приведенные в квадратных скобках, для этого выразим напряжения 
и 
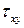через перемещения 
и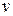 
. Тогда напряжения в пластине можно записать в форме
; 
.
Представим выражения для реакции поперечной балки на границе панели при 
(см. рис.3.2 или рис.3.5). Поперечная реакция балки 
при ее изгибе имеет вид 
, а c учетом представления функции перемещения ее можно представить в виде 
. При растяжении этой балки вдоль оси 
физическая связь между нормальной силой в ней и перемещением 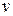запишется в форме 
, а статическое соотношение между потоком касательных сил в обшивке 
и нормальной силой имеет вид
.
Тогда статические граничные условия (3.13) и (3.14) примут вид
; (3.28)
. (3.29)
Слагаемые, описывающие реакцию балки, преобразуем к виду, содержащему упругую форму изгиба и растяжения балки и ее граничные условия. Для этого интегралы для балочных составляющих, содержащие заданные функци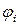и 
и 
, следует проинтегрировать по частям необходимое число раз. Тогда выражения (3.28) и (3.29) можно переписать в виде
;
.
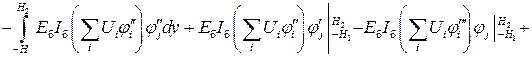
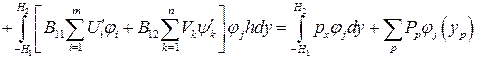Нужно отметить, что на границах балки выражения приобретают конкретный смысл и их можно представить как 
; 
; 
, где
- момент, перерезывающая и нормальная силы на концах балки, где она имеют контакт с продольными элементами. Удовлетворяя условия контакта, запишем: 
; 
; 
, где 
– соответствующие силовыефакторы в продольном элементе в месте их стыка (индекс 
соответствует продольным элементам). Для продольного элемента силовые факторы можно раскрыть через выражения перемещений в местах контакта с поперечной балкой. Если принять, что продольный элемент работает на растяжение-сжатие, то напряжения будут постоянны по сечению и силовые факторы примут вид 
; 
и 
или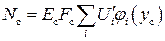 
. Если необходимо учесть момент в продольных элементах, то необходимо, чтобы выбранные функции перемещений учитывали их изгиб. Без учета изгибающих моментов статические граничные условия примут вид
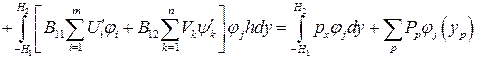; (3.30)
. (3.31)
Если для балочных функций перемещений граничные условия на свободном краю уже удовлетворены, то в выражениях (3.30) и (3.31) умножение проводится только на функции, учитывающие депланацию поперечных сечений. Эти условия можно использовать и в смешанных граничных условиях, где часть края закреплена, а часть свободна от закрепления (см. рис.3.1), что отражается на границах интегрирования и выборе функци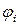й и с учетом выполнения кинематических условий.
Теперь рассмотрим смешанные граничные условия, представленные рис. 3.1, где панель закреплена в точках 
и 
, а между ними край свободен от нагрузки. Сначала удовлетворим условие закрепления панели и для этого выпишем выбранные функции перемещений
;
.
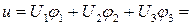
Здесь функци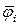и 
и 
в соответствии с методом В.З. Власова уже удовлетворяют геометрическим граничным условиям на краю 
, и поэтому необходимо удовлетворить условие закрепления для выражений, содержащих балочные составляющие перемещений 
и 
. Для этого отделим балочные функции от остальных 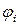и и перепишем выражения для перемещений и 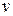в виде
;
.
Тогда из этого представления видно, что для удовлетворения условия закрепления панели необходимо, чтобы выражения в квадратных скобках равнялись нулю, т. е.
; 
. (3.32)
При выбранных шести функциях решения на этом краю необходимо записать еще четыре граничных условия. Так как геометрические граничные условия уже удовлетворены, то запишем статические граничные условия на краю . Эти условия имеют прежний вид (3.30) и (3.31), но при значениях 
и 
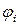на краю и для функций и , учитывающих только депланацию поперечного сечения. Таким образом, получается полная система алгебраических уравнений для нахождения констант интегрирования дифференциальных уравнений рассматриваемой задачи. Как показал практический расчет, если при точечной заделке поперечный край подкреплен балкой, то в зависимости от ее изгибной жесткости этот край может приближаться по своим свойствам к жесткой заделке. Поэтому в зависимости от требования к условиям крепления конструкции и распределения нагрузки в этом месте можно менять параметры поперечного подкрепления для регулирования перемещения на свободном краю между точками крепления. В случае закрепления края по всей высоте граничные условия будут геометрическими и записаны при в виде
;
или
и 
, (3.33)
откуда и будет определена необходимая половина констант задачи.
Дополнительный анализ граничных условий будет сделан при рассмотрении конкретных примеров определения напряженно-деформированного состояния.
