В соответствии с методом В.З. Власова функции перемещений 
и 
и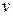щем в виде следующих рядов:
; 
. (3.3)
Здесь функции 
и 
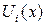, называемые аппроксимирующими, выбираются с учетом условий нагружения и закрепления панели, а функции 
и 
подлежат определению в процессе решения задачи. Так как задача решается в перемещениях, то выбираемые функции должны быть непрерывными и должны удовлетворять геометрическим граничным условиям, если таковые имеются.
Примем физические уравнения в следующем виде:
для ортотропной пластины
(3.4)
для подкрепляющих элементов
.
Здесь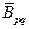 
- средние значения упругих констант пластины, вычисление которых приведено в [1]; 
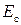и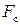 
- модуль упругости и площадь поперечного сечения подкрепляющих элементов.
Учтем, что усилия и жесткости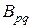 
в пластине
; 
; 
; 
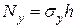. (3.5)
Подставляя в (3.4) и (3.5) формулы для перемещений (3.3) и полученные выражения в (3.1) и (3.2), запишем полную энергию Э в виде
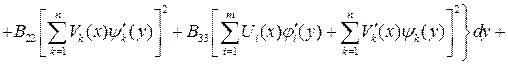
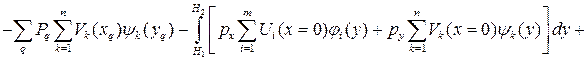
. (3.6)
Так как функции , известны, то полная энергия 
превратится в следующий функционал:
.
Минимум этого функционала в соответствии с принципом Лагранжа будет реализовываться уравнениями Эйлера-Лагранжа, которые являются по физическому смыслу уравнениями равновесия:
; (3.7)
, (3.8)
а естественные граничные условия представляют обобщенные статические граничные условия
и 
. (3.9)
Здесь 
и 
содержат слагаемые внешних нагрузок, входящие в работу внешних сил (3.2).
Уравнения равновесия в перемещениях с использованием соотношений (3.7) и (3.8) в каноническом виде записываются как
; (3.10)
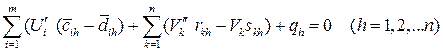, (3.11)
где коэффициенты уравнений равновесия имеют вид
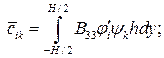
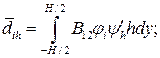
(3.12)
и учитывают все плоские формы деформации обшивки. Здесь 
- полная ширина панели, продольная ось 
делит панель пополам 
, а естественные граничные условия (3.9) запишутся как
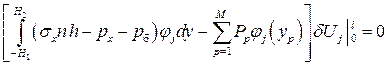; (3.13)
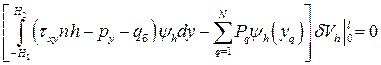, (3.14)
где 
и 
- реакция поперечного силового элемента от действующих на него сил; n - нормаль к поверхности на рассматриваемой границе.
Решение канонической системы уравнений равновесия в общем случае нагружения и граничных условий чаще всего связано с математическими трудностями. Класс задач можно существенно расширить и упростить решение, если это решение представлять в симметричной или кососимметричной форме. Для плоских панелей естественно рассматривать задачи чистого растяжения и задачи поперечного изгиба отдельно. Необходимо оговорить, что конструкция тоже отвечает этим же условиям. Чаще всего рассматриваемые конструкции обладают продольной симметрией формы, что и позволяет общие задачи разлагать на простые составляющие и использовать одни и те же математические функции для решения. Кроме того, с помощью ортогонализации выбираемых функций и 
можно добиться того, что некоторые необходимые коэффициенты уравнений равновесия будут равны нулю, а решение системы существенно упростится. Аналитическое решение системы (3.10) и (3.11) возможно, если число выбираемых функций не больше четырех.
Рассмотрим выбор расчетных функций и их систематизацию с учетом представляемых задач.
