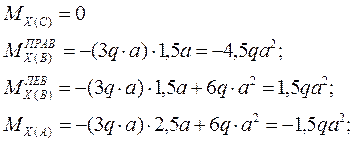ИЗГИБ.
Нейтральный слой
ВИДЫ ИЗГИБА.
1.Плоский и пространственный
2.Прямой и косой
3.Чистый и поперечный.
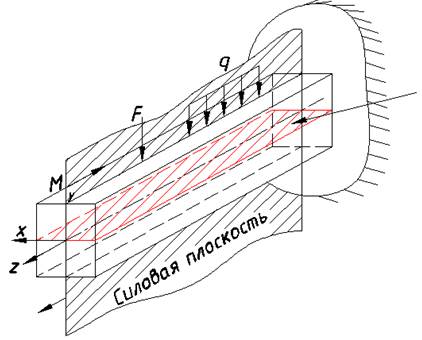
Изгиб, при котором все силы лежат в одной плоскости называется плоским.
Изгиб, при котором силы лежат в двух или нескольких плоскостях называется пространственным.
Изгиб, при котором силовая плоскость совпадает с одной из плоскостей симметрии бруса (главной плоскостью) называется прямым.
Изгиб, при котором силовая плоскость не совпадает ни с одной из плоскостей симметрии бруса называется косым.
Изгиб, при котором в поперечных сечениях бруса возникает только один внутренний силовой фактор - Мизг - называется чистым.
Изгиб, при котором в поперечных сечениях бруса возникают одновременно два внутренних силовых фактора называется поперечным. (Qy и Мизг)
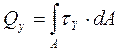
Поперечная сила Qу – результирующая всех внутренних касательных сил, возникающих в поперечных сечениях бруса.
Изгибающий момент Мх – результирующий момент всех внутренних нормальных сил, возникающих в поперечных сечениях бруса, относительно нейтральной оси поперечного сечения.
Поперечная сила Qу, численно равна алгебраической сумме внешних сил, действующих по одну сторону от рассматриваемого сечения.
Если внешние силы стремятся повернуть отсеченную часть балки по часовой стрелке относительно точки, через которую проходит сечение, то ей присваивается знак (+), а в противоположную знак (-).
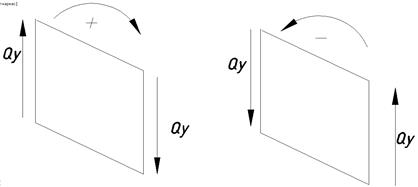
| соответствует вращению часовой стрелки | соответствует вращению против часовой стрелки |
Изгибающий момент Мх в произвольном поперечном сечении балки численно равен алгебраической сумме моментов внешних сил, действующих по одну сторону от рассматриваемого сечения, относительно точки, через которую проходит сечение.
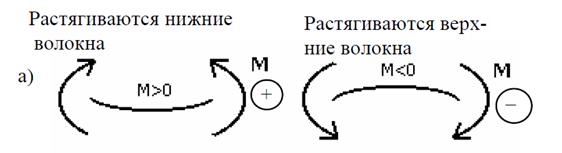
Если внешняя сила стремится изогнуть отсеченную часть балки по часовой стрелке относительно точки, через которую проходит сечение, выпуклостью вниз, то ей присваивается знак (+), а выпуклостью знак (-).
ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИНТЕНСИВНОСТЬЮ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ Q, ПОПЕРЕЧНОЙ СИЛОЙ QУ И ИЗГИБАЮЩИМ МОМЕНТОМ МХ.
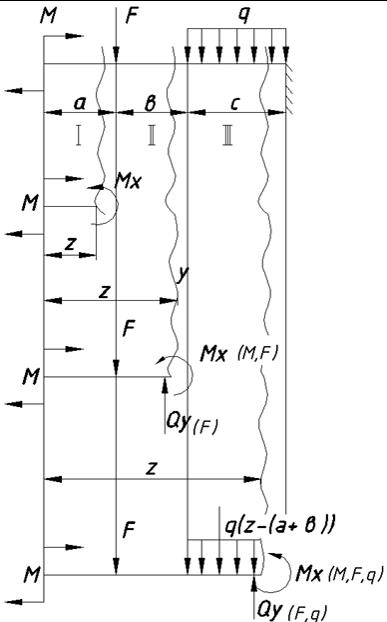
На балку действует равномерно распределенная нагрузка q.
Под действием внешней нагрузки в опорах балки возникают реакции Х и У а, У в. Учитывая, что нагрузка направлена вертикально составляющая реакции в опоре А будет Х = 0
Предполагаем, что реакции У а, У в нами определены.
Рассечем балку сечением, отстоящим от опоры А на расстоянии Z, и вторым сечением, расположенным на расстоянии dZ от первого сечения.
Поперечнаяая сила в первом сечении равна: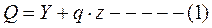 
Во втором сечении: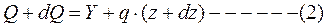 
Изгибающий момент в первом сечении равен: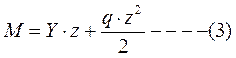 
Во втором сечении: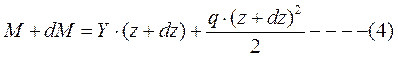 
Вычтем из уравнения (4) уравнение(3)
отсюда получим: 
Полученная дифференциальная зависимость формулируется следующим образом:
Поперечная сила в любом сечении балки может быть найдена как производная от изгибающего момента в этом сечении по абсциссе z.
Вычтем из уравнения (2) уравнение(1)
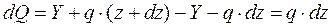
отсюда получим новую дифференциальную зависимость: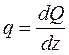 
Она означает, что распределенная нагрузка, действующая в произвольном сечении балки может быть найдена как производная от перерезывающей силы в этом сечении по абсциссе z.
Можно записать общую зависимость: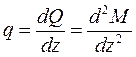 
; 
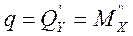
Распределенная нагрузка, действующая в произвольном сечении балки может быть найдена как вторая производная от изгибающего момента, действующего в этом сечении по абсциссе z.
ПРАВИЛА ПОСТРОЕНИЯ ЭПЮР.
1.Если q=0(распределенная нагрузка отсутствует), то Qу=const (на эпюре: горизонтальная прямая), Мх является линейной функцией (на эпюре: наклонная прямая).
2.Если q=const, то Qy является линейной функцией (на эпюре: наклонная прямая), а Мх является квадратной функцией (на эпюре: парабола).
3.Выпуклость параболы направлена в сторону противоположную направлению нагрузки q.
4.Если Qy>0, то Мх – возрастает слева направо;
Qy<0, то Мх – убывает слева направо;
Qy=0, то Мх = const, - чистый изгиб.
5.Если к балке приложена сосредоточенная сила, то в соответствующем сечении поперечная сила Qу изменяется скачкообразно на величину силы, а на эпюре Мх образуется характерный излом (смежные участки эпюры мх сопрягаются не плавно)
6.В том месте, где к балке приложен сосредоточенный момент, на эпюре Мх, образуется скачок на величину этого момента, а на эпюрах q и Qу это не отражается.
7.На свободном или шарнирно опертом конце балки изгибающий момент Мх=0, если там не приложен сосредоточенный момент. Если же сосредоточенный момент приложен, то изгибающий момент Мх = Мi.
8.В заделке сила реакции и реактивный момент численно равны соответственно поперечной силе и изгибающему моменту в этом сечении.
Рассмотрим консольную балку, нагруженную двумя силами.
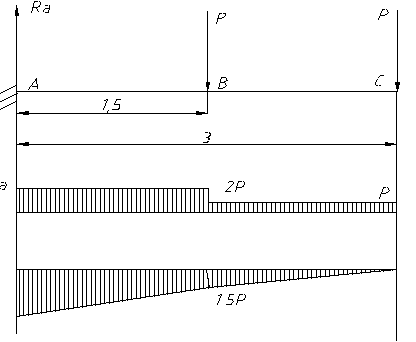
Задача. Построить эпюры Qy и Мх по длине балки. 
1.Определим значения поперечных сил Qy в характерных точках А, В, С и построим эпюру Qy.
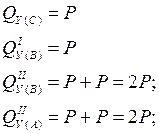
Реакция в точке А равна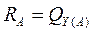 
2. Определим значения изгибающих моментов Мх в характерных точках А, В, С и построим эпюру Мх.
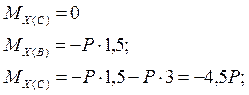
Задача. Построить эпюры Qy и Мх по длине балки.
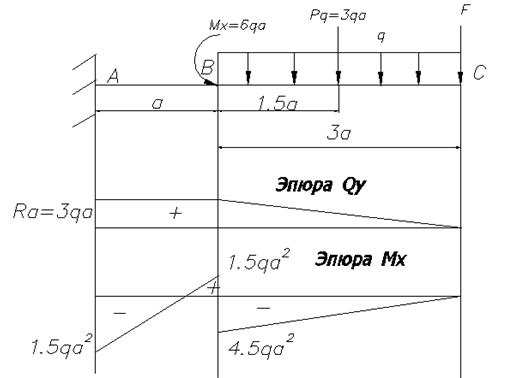
1.Определим значения поперечных сил Qy в характерных точках А, В, С и построим эпюру Qy.
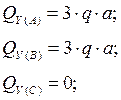Реакция в точке А равна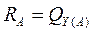
2. Определим значения изгибающих моментов Мх в характерных точках А, В, С и построим эпюру Мх.
