П. 4 Системы дифференциальных уравнений.
Общие понятия. Нормальные системы.
Определение. Системой ДУ называется совокупность уравнений, в каждое из которых входят независимая переменная t, искомые функции и их производные.
Примеры.
1) 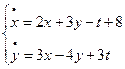 , где
, где 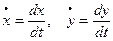 .
.
2)  , 3)
, 3) 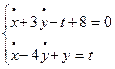 , 4)
, 4) 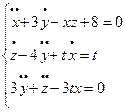 . 5)
. 5) 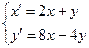 .
.
Определение. Нормальной системой n ДУ 1-гго порядка с n неизвестными называется система уравнений вида:
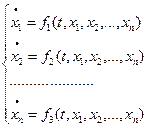 .
. 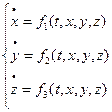 – система трех ДУ 1-го порядка с 3 неизвестными (*).
– система трех ДУ 1-го порядка с 3 неизвестными (*).
В примере это1, 2 и 5 системы.
Замечание. Рассмотрим лишь системы трех линейных ДУ 1-го порядка с 3 неизвестными.
Определение. Общее решение нормальной системы трех линейных уравнений с тремя неизвестными имеет вид: 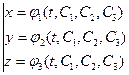 , где С 1, С 2, С 3 – произвольные постоянные. (**)
, где С 1, С 2, С 3 – произвольные постоянные. (**)
Замечание 1. Количество произвольных постоянных системы ДУ 1-го порядка равно количеству неизвестных функций системы.
Замечание 2. В выражения некоторых искомых функций могут входить не все произвольные постоянные. Но в общем решении должны присутствовать все произвольные постоянные, например, 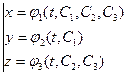 .
.
Задача Коши. Начальные условия для системы (*): 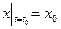 ,
, 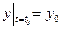 ,
, 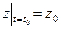 . Для нахождения частного решения системы (*), подставляем начальные условия в общее решение (**). Получим систему алгебраических уравнений для определения произвольных постоянных. Определитель данной системы – вронскиан.
. Для нахождения частного решения системы (*), подставляем начальные условия в общее решение (**). Получим систему алгебраических уравнений для определения произвольных постоянных. Определитель данной системы – вронскиан.
Теорема Коши. Если правые части нормальной системы (*) непрерывны вместе со своими частными производными в окрестности значений t 0, х 0, y 0, z 0 , то существует единственная система функций x (t), y (t), z (t), являющаяся решением системы и удовлетворяющая заданным начальным условиям.
Замечание. Механическая иллюстрация решений нормальной системы двух линейных ДУ с двумя неизвестными  .
.
Пусть (х, у) – координаты точки на плоскости (Оху), которую называют фазовой плоскостью.
Параметрическое уравнение х = x (t), y = y (t) – параметрическое задание линии на фазовой плоскости. Если t – время, то функции х = x (t), y = y (t) выражают законы движения проекций движущейся точки на оси координат, линия х = x (t), y = y (t) – траектория движения, 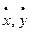 – проекции скорости движущейся точки на оси координат.
– проекции скорости движущейся точки на оси координат.
Определение. Неоднородной нормальной системой (ННС) трех линейных дифференциальных уравнений 1-го порядка с постоянными коэффициентами с тремя неизвестными называется система вида: 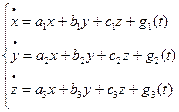 .
.
Определение. Однородной нормальной системой (ОНС) трех линейных дифференциальных уравнений 1-го порядка с постоянными коэффициентами с тремя неизвестными называется система вида: 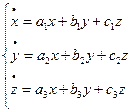 . (1)
. (1)
Замечание. Рассмотрим решение только однородных нормальных систем трех (двух) линейных дифференциальных уравнений 1-го порядка с постоянными коэффициентами.
Определение. Общим решением ОНС называется 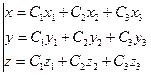 . (2)
. (2)
Замечание (Задача Коши). Для нахождения частного решения надо подставить заданные начальные условия 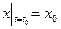 ,
, 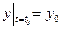 ,
, 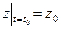 в общее решение (2). В итоге получим систему алгебраических уравнений для определения произвольных постоянных. Данная система будет иметь решение тогда и только тогда, когда определитель данной системы – вронскиан – не будет равен нулю ни при каких значениях t 0:
в общее решение (2). В итоге получим систему алгебраических уравнений для определения произвольных постоянных. Данная система будет иметь решение тогда и только тогда, когда определитель данной системы – вронскиан – не будет равен нулю ни при каких значениях t 0: 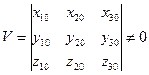 .
.
Определение. Совокупность трех частных решений, удовлетворяющих условию 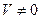 . Образуют фундаментальную систему решений.
. Образуют фундаментальную систему решений.
Определение. Матрица 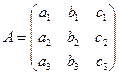 – матрица нормальной НОС (1).
– матрица нормальной НОС (1).
Определение. Уравнение det (A – rE) = 0 или 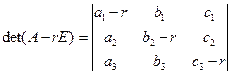 =0 (3)
=0 (3)
называется характеристическим уравнением системы, числа ri, i = 1, 2, 3, называются собственными числами.
Решение ОНС трех уравнений ДУ (1).
1 метод. Сведение к одному ДУ.
Нормальная однородная система может быть заменена одним однородным ДУ, порядок которого равен числу уравнений системы. (Нормальные неоднородные системы ДУ сводятся к неоднородным уравнениям).
И обратно, одно ДУ n -го порядка, разрешенное относительно старшей производной, с помощью введения новых вспомогательных функций всегда можно свести к нормальной системе, например, уравнение 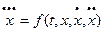 с помощью вспомогательных функций
с помощью вспомогательных функций 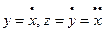 сводится к системе
сводится к системе 






