Лекция 1.
Основные понятия.
Пусть D – область n -мерного пространства Rn точек х=(х1,х2,…,хn), где n≥2.
Наиболее общее уравнение в частных производных k -порядка от n независимых переменных х1,х2,…,хn можно записать в следующем виде
(1)
где k1+ k2+…+ kn=k, u=u(х)=u(х1,х2,…,хn) – неизвестная функция 
-заданная функция от своих аргументов.
D - область задания уравнения (1).
Примеры:
1. 
– уравнение 1-ого порядка;
2. 
– уравнение 2-ого порядка;
3. 
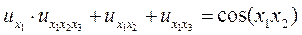– уравнение 3-ого порядка.
Определение: Уравнение в частных производных называется уравнением k -ого порядка, если оно содержит, хотя бы одну частную производную k -го порядка и не содержит производных более высокого порядка.
Определение: Определенная в области D функция u(х)=u(х1,х2,…,хn), непрерывная вместе со своими частными производными, входящими в это уравнение, и обращающая его в тождество по независимым переменным х1,х2,…,хn , называется классическим решением или просто решением дифференциального уравнения (1).
Если размерность пространства 
равна 2, то есть n=2, то в дальнейшим будем писать
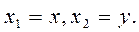
Если n=3, то
Примеры:
1. Проверить, являются ли следующие функции:
а)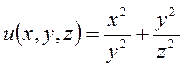 
;
б) 
;
решениями уравнения 
в области: x>0, y>0,,z>0.
Решение: 1) Вычислим u x, u y u z.
.
Подставив в исходное уравнение, получим
.
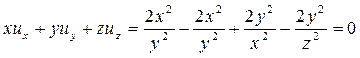Следовательно: функция 
в указанной области является решением данного уравнения.
2) Также найдем частные производные: ux=yz; uy=xz; uz=xy и подставим в исходное уравнение:
при x>0,y>0,z>0.
Вывод: функция u=xyz не является решением исходного уравнения при x>0,y>0,z>0.
Дифференциальное уравнение в частных производных также, как и обыкновенное дифференциальное уравнение, в большинстве случаев имеет бесконечное множество частных решений, то есть определяет некоторое семейство функций, удовлетворяющих данному уравнению.
Совокупность таких функций образует общее решение дифференциального уравнения в частных производных.
Между общими решениями обыкновенного дифференциального уравнения и общими решениями дифференциального уравнения в частных производных имеется существенное различие.
Как известно, общее решение обыкновенного дифференциального уравнения
, где у=у(х)
представляет собой семейство функций, зависящее от 2-х произвольных постоянных:
.
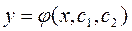Пример:
1) 
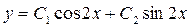, где С1,С2 – произвольные постоянные.
Для их нахождения достаточно задать начальное условие: например у(0)=0,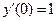 
. И получим С1 =0, С2 = 
.
.
Рассмотрим любое дифференциальное уравнение в частных производных первого порядка с двумя независимыми переменами х и у, не содержащей производной либо по х, либо по у.
Пусть
При вычисление 
считаем фиксированной (постоянной).
При фиксированной у исходное дифференциальное уравнение можно рассматривать как обыкновенное дифференциальное уравнение с искомой функцией u и независимой переменной х.
Пусть общее решение обыкновенного дифференциального уравнения определяется по формуле
.
Это решение содержит у как параметр и оно при постоянном С является решением исходного дифференциального уравнения.
Для того, чтобы полученная функция 
была решением исходного дифференциального уравнения в частных производных необходимо и достаточно, чтобы С было постоянным относительно х, то есть она может быть любой функций от у.
Тем самым получим наиболее общее решение дифференциального уравнения в частных производных первого порядка, если поставим на место С произвольную функцию от у, например, 
:
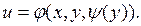
Таким образом, общее решение дифференциального уравнения в частных производных первого порядка содержит одну произвольную функцию из класса С(R) непрерывных функций.
Примеры:
1. 
Решение: перепишем данное уравнение в следующем виде:
и у рассмотрим как параметр.
Последнее уравнение представляет линейное уравнение первого порядка. Его общее решение
Тогда общее решение дифференциального уравнения в частных производных определяется по формуле
.
У дифференциальных уравнениях в частных производных более высоких порядков общее решение содержит произвольные функции, количество которых, вообще говоря, равно порядку уравнения.
Пример:
,
найти общее решение. Для этого представим в виде 
. Отсюда следует 
, где С1(у) – произвольная непрерывная функция.
Интегрируя последнее уравнение, получим
,
где С2(х) – произвольная функция
или
,
где f(x)=C2(x),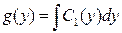 
.
Исходя из общего решения дифференциального уравнения в частных производных можно найти частное решение. Для этого надо найти конкретный вид функции f и g на основании заданных условий рассматриваемой задачи.
Надо отметить, что для только малого числа дифференциальных уравнений в частных производных удается построить в явном виде общее решение. В теории дифференциальных уравнениях в частных производных созданы методы непосредственного нахождения частных решений дифференциальных уравнений, удовлетворяющих определенным начальным и граничным условиям.
Многие задачи физики и механики приводят к исследованию дифференциальных уравнений в частных производных.
Примеры:
1) Выяснить, является ли приведенные ниже равенства дифференциальными уравнениями в частных производных?
а)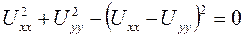 
б) 
в) 
2) Решить дифференциальные уравнения первого порядка.
а)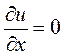 
б) 
в) 
г) 
д)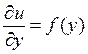 
е) 
ё)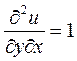 
3) Определить порядок дифференциального уравнения в частных производных.
4) Проверить, что функция
а) 
есть решение уравнения 
.
б)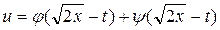 
есть решение уравнения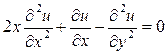 
Самостоятельно.
1) 
2) 
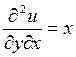
3) 
4) 
5) 
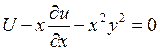
6) 
.
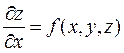Лекция 2.
