Уравнения высших порядков
Это уравнения вида
 , (5)
, (5)
здесь  ,
,  – постоянные;
– постоянные;  – непрерывные функции от х.
– непрерывные функции от х.
Теорема1. Общее решение неоднородного уравнения (5) представляется как сумма какого-нибудь частного решения этого уравнения  и общего решения
и общего решения 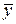 соответствующего однородного уравнения
соответствующего однородного уравнения  , т.е.
, т.е.  ,.
,.
Частное решение  можно находить методом подбора по правой части
можно находить методом подбора по правой части  или методом вариации произвольных постоянных.
или методом вариации произвольных постоянных.
1. Пусть  уравнения (5) имеет вид
уравнения (5) имеет вид 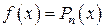 , тогда
, тогда
а) если нуль не является корнем характеристического уравнения, то 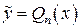 , где
, где  – многочлен с неопределенными коэффициентами;
– многочлен с неопределенными коэффициентами;
б) если нуль – корень характеристического уравнения кратности  , то частное решение ищем в виде
, то частное решение ищем в виде  , где
, где  – многочлен с неопределенными коэффициентами.
– многочлен с неопределенными коэффициентами.
2. Пусть в правой части дифференциального уравнения стоит функция 
 , где
, где  – многочлен от
– многочлен от  ; тогда надо различать два случая:
; тогда надо различать два случая:
а) если  не является корнем характеристического уравнения, то частное решение следует искать в виде
не является корнем характеристического уравнения, то частное решение следует искать в виде  , где
, где  – многочлен той же степени, что и
– многочлен той же степени, что и  , но с неопределенными коэффициентами;
, но с неопределенными коэффициентами;
б) если  есть корень кратности
есть корень кратности  характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде
характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде  , где
, где  – многочлен той же степени, что и
– многочлен той же степени, что и  .
.
3. Пусть правая часть уравнения имеет вид 
 , где
, где  и
и  – многочлены. Тогда вид частного решения определяется следующим образом:
– многочлены. Тогда вид частного решения определяется следующим образом:
а) если число  не есть корень характеристического уравнения, то частное решение имеет вид
не есть корень характеристического уравнения, то частное решение имеет вид  , где
, где  и
и  – многочлены с неопределенными коэффициентами,
– многочлены с неопределенными коэффициентами,  ;
;
б) если число  есть корень характеристического уравнения кратности
есть корень характеристического уравнения кратности  , то
, то  .
.
4. Пусть  , где
, где  и
и  – многочлены от х. Тогда:
– многочлены от х. Тогда:
а) если число  не является корнем характеристического уравнения, то частное решение ищем в виде
не является корнем характеристического уравнения, то частное решение ищем в виде  , где
, где  и
и  – многочлены с неопределенными коэффициентами, где
– многочлены с неопределенными коэффициентами, где  ;
;
б) если число  является корнем кратности
является корнем кратности  характеристического многочлена, то частное решение ищем в виде
характеристического многочлена, то частное решение ищем в виде 
 , где
, где  и
и  имеют тот же смысл, что и в случае а).
имеют тот же смысл, что и в случае а).
Таким образом, методом подбора решаются дифференциальные уравнения (1.7), имеющие правую часть вида 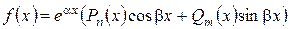 , где
, где  и
и  – многочлены степеней
– многочлены степеней 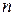 и
и  ;
;  и
и  – числа.
– числа.
Вид частного решения  повторяет вид правой части
повторяет вид правой части 
 , где
, где  – кратность, с которой
– кратность, с которой  (
( и
и  взяты из правой части) встречается среди корней характеристического уравнения;
взяты из правой части) встречается среди корней характеристического уравнения; 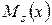 и
и  – многочлены с неопределенными пока коэффициентами, где
– многочлены с неопределенными пока коэффициентами, где 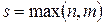 .
.
Пример 8. Найти общее решение линейного неоднородного дифференциального уравнения (ЛНДУ) 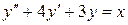 .
.
Запишем общее решение  соответствующего линейного однородного дифференциального уравнения (ЛОДУ)
соответствующего линейного однородного дифференциального уравнения (ЛОДУ)  :
:  .
.
Правая часть ЛНДУ – многочлен первой степени, число нуль не является корнем характеристического уравнения  . Значит, частное решение будем искать в виде
. Значит, частное решение будем искать в виде 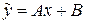 .
.
Подставим 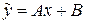 ,
, 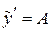 ,
,  в дифференциальное уравнение:
в дифференциальное уравнение:  . Приравнивая коэффициенты при одинаковых степенях
. Приравнивая коэффициенты при одинаковых степенях  , получим
, получим  Решая эту систему, найдем
Решая эту систему, найдем  ,
,  .
.
Тогда  .
.
Общее решение  будет иметь вид
будет иметь вид  .
.
Пример 9. Найти общее решение ЛНДУ 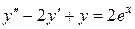 .
.
Запишем общее решение  соответствующего ЛОДУ:
соответствующего ЛОДУ:  .
.
Правая часть ЛНДУ имеет вид  , причем число
, причем число  является корнем характеристического уравнения
является корнем характеристического уравнения  кратности 2.
кратности 2.
Значит, частное решение ЛНДУ будем искать в форме  , т.е.
, т.е.  . Производные
. Производные 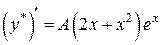 ,
,  подставим в ЛНДУ и сравнивая коэффициенты при одинаковых степенях, получим
подставим в ЛНДУ и сравнивая коэффициенты при одинаковых степенях, получим  , т.е.
, т.е.  .
.
Общее решение  будет иметь вид
будет иметь вид  .
.
Пример 10. Найти частное решение дифференциального уравнения  ,
,  ,
,  .
.
Решение. Решим соответствующее однородное уравнение:  . Характеристическое уравнение
. Характеристическое уравнение  ,
,  ,
,  . Решение однородного уравнения
. Решение однородного уравнения  . Вид частного решения
. Вид частного решения  (метод подбора по правой части). Определим коэффициент
(метод подбора по правой части). Определим коэффициент  :
:
 ,
,  .
.
Подставляя в данное уравнение  и
и  , получим:
, получим:
 ,
,  .
.
Общее решение дифференциального уравнения:  .
.
Определим константы  и
и  , т.е. решим задачу Коши:
, т.е. решим задачу Коши:
 ,
, 
 ,
,  .
.
Ответ:  .
.
Пример 11. Найти общее решение ЛНДУ  .
.
Характеристическое уравнение  соответствующего ЛОДУ имеет корни
соответствующего ЛОДУ имеет корни  , следовательно, общее решение ЛОДУ есть
, следовательно, общее решение ЛОДУ есть  .
.
Правая часть ЛНДУ имеет вид  , т.е. число
, т.е. число 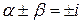 не является корнем характеристического уравнения. Поэтому частное решение ЛНДУ ищем в виде
не является корнем характеристического уравнения. Поэтому частное решение ЛНДУ ищем в виде  или
или 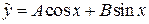 , где
, где  и
и  определяются после подстановки
определяются после подстановки 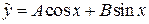 ,
,  ,
,  в исходное ЛНДУ:
в исходное ЛНДУ:
 .
.
Приравнивая коэффициенты при  и
и  в обоих частях, получим
в обоих частях, получим  ,
,  , откуда
, откуда 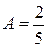 ,
,  .
.
Общее решение 
 .
.
Пример 12. Найти общее решение дифференциального уравнения  .
.
Характеристическое уравнение  имеет четыре корня:
имеет четыре корня:  ,
,  ,
,  ,
,  , следовательно, общее решение
, следовательно, общее решение  соответствующего ЛОДУ
соответствующего ЛОДУ  .
.
Правая часть  представляет собой
представляет собой  . Так как нуль не является корнем характеристического уравнения, то частное решение ЛНДУ повторяет вид правой части и ищется в виде
. Так как нуль не является корнем характеристического уравнения, то частное решение ЛНДУ повторяет вид правой части и ищется в виде  .
.
Дифференцируя  четыре раза и подставляя полученные выражения в дифференциальное уравнение, получим
четыре раза и подставляя полученные выражения в дифференциальное уравнение, получим  .
.
Приравнивая коэффициенты при одинаковых степенях  будем иметь
будем иметь  . Таким образом, общее решение ЛНДУ примет вид
. Таким образом, общее решение ЛНДУ примет вид
 .
.




