Дифференциальные уравнения
Типы дифференциальных уравнений
Порядок ДУ – порядок старшей производной или старшего дифференциала.  – ДУ порядка 1.
– ДУ порядка 1.
Решение – функция, обращающая ДУ в верное равенство. Проверка решения производится подстановкой.
Общее решение – совокупность всех решений, общий вид любого решения.
Задача Коши – найти решение с заданным начальным значением.
Дифференциальные уравнения первого порядка
ДУ с разделяющимися переменными (УРП) имеет вид  или
или  .
.
Пример. Найти общее решение дифференциального уравнения  .
.
В уравнении  ,
,  , значит, это УРП. Запишем в виде
, значит, это УРП. Запишем в виде 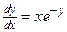 . Разделяем переменные
. Разделяем переменные  . Проинтегрируем
. Проинтегрируем 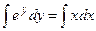 или
или  . Получим общее решение
. Получим общее решение  .
.
Пример. Найти решение ДУ  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 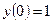 .
.
Данное уравнение по виду УРП: 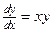 . Разделяем переменные
. Разделяем переменные  . Проинтегрируем
. Проинтегрируем 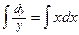 или
или  (
( ). Выразим
). Выразим  , получим общее решение
, получим общее решение 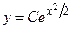 .
.
Найдем частное решение. Подставим  и
и  в ДУ и вычислим
в ДУ и вычислим  :
:  или
или  . Итак,
. Итак,  .
.
Линейное неоднородным ДУ (ЛНДУ) первого порядка  .
.
Линейное однородное ДУ (ЛОДУ) первого порядка  .
.
Построение общего решения линейного ДУ
1) Найти  общее решение ЛОДУ.
общее решение ЛОДУ.
2) Общее решение ЛНДУ ищем в похожем виде  .
.
3) Из уравнения  находим
находим  , подставляем в вид решения.
, подставляем в вид решения.
Пример. Найти общее решение для  .
.
Данное уравнение по виду ЛНДУ:  ,
,  .
.
Соответствующее ЛОДУ  . Его общее решение
. Его общее решение  .
.
Общее решение ЛНДУ будем искать в виде  . Находим
. Находим  из уравнения
из уравнения  :
:  . Подставим
. Подставим  в
в  , получим
, получим  – общее решение.
– общее решение.
Дифференциальные уравнения высших порядков
Понижение порядка – основной метод решения уравнений высших порядков.
Уравнения вида y(n) = f(x) – 
Пример. Решить 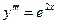 с начальными условиями x0 = 0; y0 = 1;
с начальными условиями x0 = 0; y0 = 1; 


Общее решение 
Подставим начальные условия: 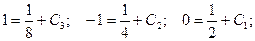
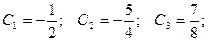
Получаем частное решение (решение задачи Коши): 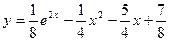 .
.
Уравнения, не содержащие явно искомой функции и ее производных до порядка k-1:  Для понижения порядка на k единиц производят замену переменной:
Для понижения порядка на k единиц производят замену переменной:

Тогда получаем: 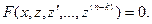
Пример. Найти общее решение уравнения 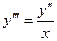 .
.
Подстановка  получим
получим 

Обратная замена: 
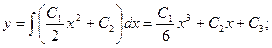
Общее решение: 
Уравнения, не содержащие явно независимой переменной: 
Порядок понижается на единицу заменой 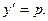
Тогда 
 и т.д.
и т.д.
Подставляя эти значения в исходное дифференциальное уравнение, получаем: 
Пример. Понизить порядок уравнения 
Замена:  получаем
получаем 
 итак, получили ДУ порядка 1.
итак, получили ДУ порядка 1.
Пример. Решить уравнение 
Подстановка 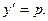 Тогда
Тогда 


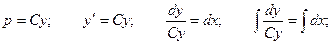

Окончательно получаем общее решение: 
Линейные дифференциальные уравнения 2 порядка
ЛНДУ 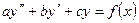 , ЛОДУ
, ЛОДУ 
Задача Коши – найти решение ДУ, удовлетворяющее начальным условиям  ,
,  .
.
Алгоритм поиска общего решения ЛОДУ
1) Найти корни характеристического уравнения – 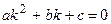 (производная заменяется степенью того же порядка).
(производная заменяется степенью того же порядка).
2) Проверить частные случаи и найти фундаментальную систему решений (ФСР):
– если  , то характеристическое уравнение имеет два вещественных различных корня
, то характеристическое уравнение имеет два вещественных различных корня 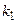 и
и  , ФСР
, ФСР  ,
,  ;
;
– если  , то характеристическое уравнение имеет один вещественный корень
, то характеристическое уравнение имеет один вещественный корень  кратности 2, ФСР
кратности 2, ФСР  ,
,  ;
;
– если  , то характеристическое уравнение имеет два комплексно-сопряженных корня
, то характеристическое уравнение имеет два комплексно-сопряженных корня 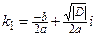 и
и  , ФСР
, ФСР  ,
,  .
.
4) Общее решение ЛОДУ  , где
, где  и
и  –произвольные постоянные.
–произвольные постоянные.
Пример. Найти общее решение дифференциального уравнения  .
.
1) Его характеристическое уравнение имеет вид  .
.
2) Так как  , то корни уравнения комплексно-сопряженные
, то корни уравнения комплексно-сопряженные  .
.
3) ФСР  ,
,  . 4) Общее решение:
. 4) Общее решение:  .
.
Пример. Найти решение ДУ  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 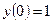 ,
,  .
.
1) Его характеристическое уравнение имеет вид  .
.
2) Так как  , то уравнение имеет два различных вещественных корня
, то уравнение имеет два различных вещественных корня  ,
,  .
.
3) ФСР  ,
,  . 4) Общее решение:
. 4) Общее решение:  .
.
5) Найдем постоянные по начальным условиям 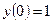 ,
,  . Вычислим:
. Вычислим:  . Подставим в общее решение и его производную
. Подставим в общее решение и его производную 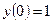 ,
,  :
:  или
или 
Решив, получаем  ,
, 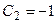 . Тогда искомое частное решение примет вид
. Тогда искомое частное решение примет вид  .
.






