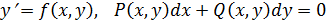 бірінші ретті дифференциалдық теңдеулерді шешу алгоритмі шешу тәсілін анықтауға көмектеседі.
бірінші ретті дифференциалдық теңдеулерді шешу алгоритмі шешу тәсілін анықтауға көмектеседі.
| № | Теңдеудің аты | Теңдеудің формуламен жазылуы + түсініктеме | Теңдеуді шешуге нұсқау |
| Қарапайым ДТ | 
| 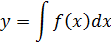
| |
| Айнымалылары ажыратылған теңдеу | 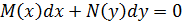
|  , ,
 – тұрақты – тұрақты
| |
| Айнымалылары ажыратылатын теңдеу | 
|  №2 №2 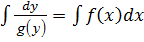
| |

|  №2 №2
| ||
| Сызықтық біртекті теңдеу | 
| 3-пунктті қараңыз: 
 (1) (1)
| |
| Сызықтық біртекті емес теңдеу | 

| Сәйкес сызықтық біртекті теңдеуді шешіңіз. (1) - дегі С-ны  -ке тәуелді функция деп есептеп, (1)-ді
5-пунктке қойыңыз: -ке тәуелді функция деп есептеп, (1)-ді
5-пунктке қойыңыз:
 (C+
+ (C+
+ 
| |
| Бернулли теңдеуі | 

| Ауыстыру: 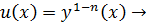

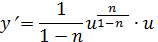
| |
| Толық дифференциалды теңдеу |  , мұндағы , мұндағы 
|  немесе немесе

|
Тапсырма 1. 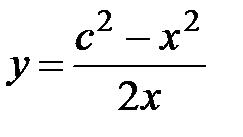 функциясының
функциясының 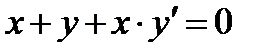 теңдеудің шешімі болатындығын, болмайтындығын тексеріңіз.
теңдеудің шешімі болатындығын, болмайтындығын тексеріңіз.
Шешуі.
Функцияның туындысын табамыз:
 .
.
Берілген теңдеуге  және
және  мәндерін қоямыз:
мәндерін қоямыз:
 .
.
Жауабы: берілген функция теңдеудің шешімі болады.
Тапсырма 2. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 
Шешуі.
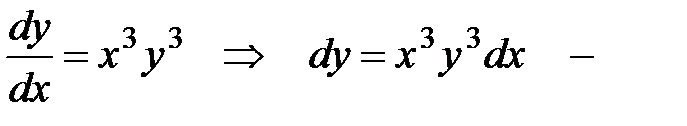 айнымалылары ажыратылатын теңдеу.
айнымалылары ажыратылатын теңдеу. 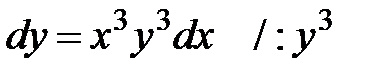


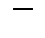 айнымалылары ажыратылған теңдеу.
айнымалылары ажыратылған теңдеу.



Жауабы: 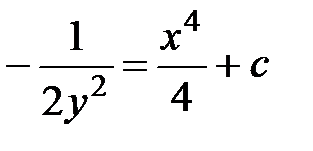
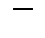 теңдеудің жалпы интегралы.
теңдеудің жалпы интегралы.
Тапсырма 3. Коши есебін шешіп, интегралдық қисықты сызыңыз:  .
.
Шешуі.

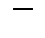 айнымалылары ажыратылатын теңдеу.
айнымалылары ажыратылатын теңдеу.

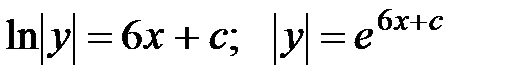
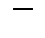 теңдеудің жалпы шешімі.
теңдеудің жалпы шешімі.
Бастапқы шарттарды қолданамыз: 

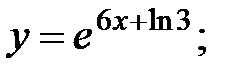

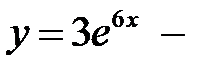 бастапқы шарттарды қанағаттандыратын дербес шешім.
бастапқы шарттарды қанағаттандыратын дербес шешім.
Жауабы:  .
.
Тапсырма 4. Коши есебін шешіңіз: 
Шешуі.

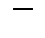 айнымалылары ажыратылатын теңдеу.
айнымалылары ажыратылатын теңдеу.
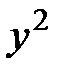
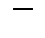 қа бөлеміз:
қа бөлеміз:  теңдеудің жалпы шешімі.
теңдеудің жалпы шешімі.
Бастапқы шарттарды қанағаттандыратын дербес шешімді іздейміз:  .
.
Ескерту. 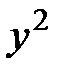
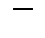 қа бөлгенде
қа бөлгенде 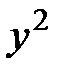 = 0 немесе
= 0 немесе  = 0 шешімін жоғалтуымыз мүмкін. Теңдеуге қою арқылы
= 0 шешімін жоғалтуымыз мүмкін. Теңдеуге қою арқылы  = 0 осы теңдеудің шешімі екендігіне көз жеткіземіз. Сонымен қатар,
= 0 осы теңдеудің шешімі екендігіне көз жеткіземіз. Сонымен қатар,  = 0 теңдеудің жалпы шешіміне кірмейтіндіктен, ерекше шешімі болады.
= 0 теңдеудің жалпы шешіміне кірмейтіндіктен, ерекше шешімі болады.
Жауабы: 
 = 0.
= 0.
Тапсырма 5. Коши есебін шешіңіз: 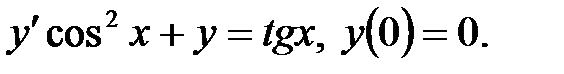
Шешуі.
Тұрақтыны вариациалау тәсілін қолданамыз. Теңдеуді 
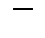 ке бөлеміз:
ке бөлеміз:
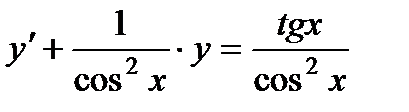
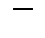 бірінші ретті сызықтық біртекті емес теңдеу.
бірінші ретті сызықтық біртекті емес теңдеу.
Сәйкес сызықтық біртекті теңдеу жазамыз:  .
.
Бұл 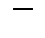 айнымалылары ажыратылатын теңдеу.
айнымалылары ажыратылатын теңдеу.


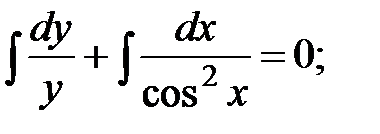
 сызықтық біртекті теңдеудің жалпы шешімі. Сызықтық біртекті емес теңдеудің шешімін
сызықтық біртекті теңдеудің жалпы шешімі. Сызықтық біртекті емес теңдеудің шешімін  түрінде іздейміз, мұндағы
түрінде іздейміз, мұндағы  белгісіз функция.
белгісіз функция.
Берілген теңдеуге 
 мәндерін қоямыз:
мәндерін қоямыз:
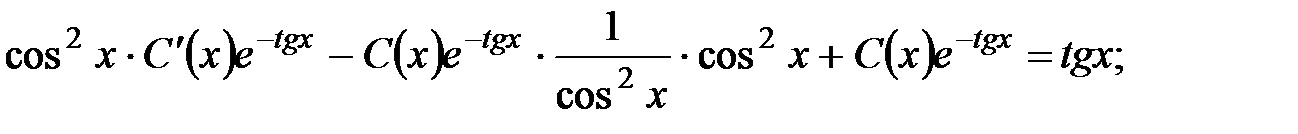

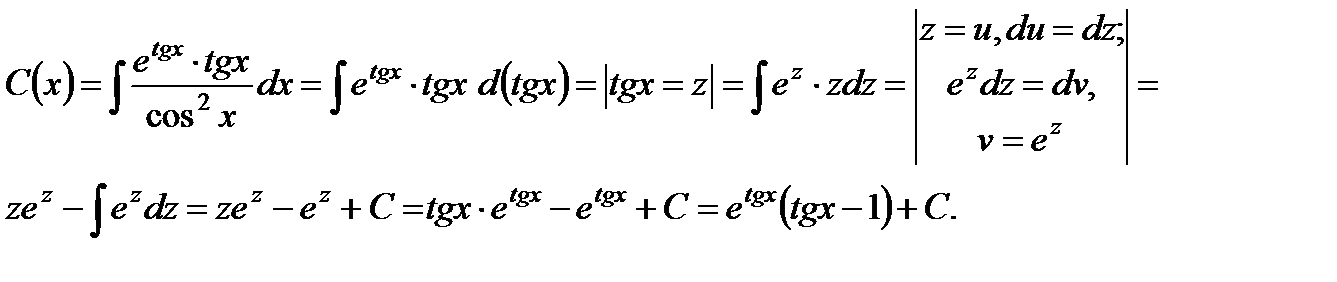
Демек,  теңдеудің жалпы шешімі.
теңдеудің жалпы шешімі.  (0) = 0 бастапқы шартын қолданамыз:
(0) = 0 бастапқы шартын қолданамыз:
0 = -1+ С; С = 1.
Жауабы: 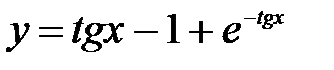 .
.
Тапсырма 6. Дифференциалдық теңдеудің жалпы шешімін табыңыз:
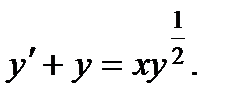
Шешуі.

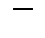 Бернулли теңдеуі.
Бернулли теңдеуі.
Ауыстыру жасаймыз: 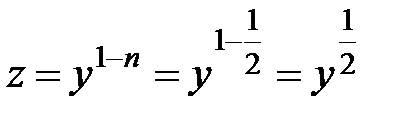 .
.  . Теңдеуге қоямыз:
. Теңдеуге қоямыз:  сызықтық теңдеу.
сызықтық теңдеу.
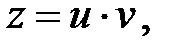


 ,
, 




 .
.
Демек,  .
.
Сонымен, 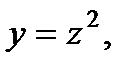 яғни
яғни  .
.
Жауабы:  .
.
Тапсырма 7. Дифференциалдық теңдеудің жалпы интегралын табыңыз: 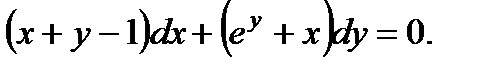
Шешуі.

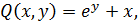



 , демек толық дифференциалдың шарттары орындалады:
, демек толық дифференциалдың шарттары орындалады:  . Белгісіз
. Белгісіз  функцияны мына формула бойынша табамыз:
функцияны мына формула бойынша табамыз:  .
.
 деп аламыз:
деп аламыз:
 .
.
 болғандықтан,
болғандықтан, 
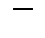 берілген теңдеудің жалпы интегралы.
берілген теңдеудің жалпы интегралы.
Жауабы: 
8 және 9 тапсырмаларды «Ретін төмендетуге болатын жоғарғы ретті дифференциалдық теңдеулер» тақырыбы бойынша құрылған төмендегі кестенің көмегімен шешуге болады.
| № | Теңдеудің формуламен жазылуы | Түсініктеме | Қажет ауыстыру (инструкция) |

| Функцияның туындысы  -ке тәуелді функция арқылы айқын түрде берілген -ке тәуелді функция арқылы айқын түрде берілген
|  рет интегралдау рет интегралдау
| |
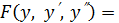 0 0
| Теңдеуде тәуелсіз айнымалы  жоқ жоқ
| 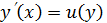 , ,
 ( ( ) )  ( ( ) )
| |
 0 0
| Теңдеуде белгісіз функция  ( ( ) жоқ ) жоқ
|  = =  , , 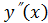 = = 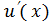
| |


| Теңдеуде белгісіз функцияның  -1 ретті туындылары жоқ -1 ретті туындылары жоқ
| 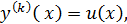
 , …, , …,

|
Тапсырма 8. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 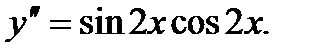
Шешуі.
Бұл теңдеу  түріндегі екінші ретті теңдеу. Екі рет интегралдау арқылы ретін төмендетеміз:
түріндегі екінші ретті теңдеу. Екі рет интегралдау арқылы ретін төмендетеміз:



Жауабы:  жалпы шешімі.
жалпы шешімі.
Тапсырма 9. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 
Шешуі.
Бұл –  функциясы айқын түрде көрсетілмеген теңдеу.
функциясы айқын түрде көрсетілмеген теңдеу.
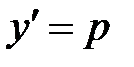 ауыстыруын қолданамыз, сонда
ауыстыруын қолданамыз, сонда  .
.
Теңдеу мына түрге келеді:  айнымалылары ажыратылатын теңдеу. Екі жағын
айнымалылары ажыратылатын теңдеу. Екі жағын  бөлеміз:
бөлеміз: 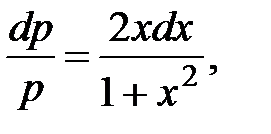

 .
.
 болғандықтан,
болғандықтан,  айнымалылары ажыратылатын теңдеу.
айнымалылары ажыратылатын теңдеу.
 жалпы шешімі.
жалпы шешімі.
Ескерту. 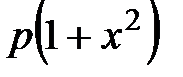
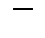 ке бөлгенде
ке бөлгенде  және
және 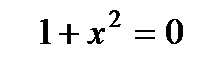 шешімдерін жоғалтып алуымыз мүмкін.
шешімдерін жоғалтып алуымыз мүмкін.  теңдеуінен
теңдеуінен  бірақ бұл шешім
бірақ бұл шешім  мәнінде жалпы шешімде бар.
мәнінде жалпы шешімде бар. 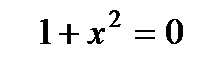 теңдеуі
теңдеуі  -тің нақты мәндерінде орындалмайды.
-тің нақты мәндерінде орындалмайды.
Жауабы: 
Тапсырма 10. Коэффициенттері тұрақты сызықтық біртекті дифференциалдық теңдеудің жалпы шешімін табыңыз.
Мұндай тапсырмаларды орындау үшін екінші ретті коэффициенттері тұрақты сызықтық біртекті дифференциалдық теңдеуді қарастырамыз:

Сипаттаушы теңдеуін жазамыз: 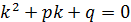 ,
, 
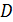
| Сипаттаушы теңдеудің түбірлері | Шешімнің фундаментальді жүйесі | Жоғарғы ретті коэффициент тері тұрақты сызықтық біртекті дифференциалдық теңдеудің жалпы шешімі
 =C1 =C1  1+C2 1+C2  2 2
|
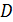 >0 >0
| 
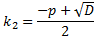
| 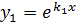 , , 
|  = C1 = C1  C2 C2 
|
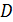 =0 =0
| 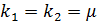 , , 
|  1= 1=  , ,
 2= 2= 
|  = C1 = C1  C2 C2 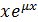 немесе немесе
 = =  С1+ C2 С1+ C2 
|
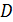 <0 <0
| 
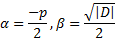
|  1= 1=  , ,  2= 2= 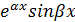
|  =C1 =C1  C2 C2 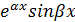 немесе немесе
 = =  C2 C2 
|
Мысал 1. 
Шешуі.
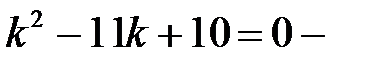 берілген теңдеудің сипаттаушы теңдеуі.
берілген теңдеудің сипаттаушы теңдеуі.
 сипаттаушы теңдеудің әртүрлі нақты түбірлері.
сипаттаушы теңдеудің әртүрлі нақты түбірлері.
Жалпы шешімі: 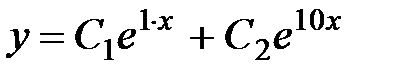 .
.
Жауабы:  .
.
Мысал 2. 
Шешуі.  сипаттаушы теңдеу.
сипаттаушы теңдеу.
 сипаттаушы теңдеудің бірдей түбірлері.
сипаттаушы теңдеудің бірдей түбірлері.
Жалпы шешімі:  .
.
Жауабы: 
Мысал 3. 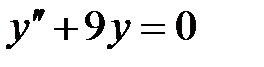
Шешуі. Сипаттаушы теңдеу құрамыз:  .
.
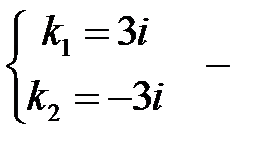 сипаттаушы теңдеудің комплекс түбірлері.
сипаттаушы теңдеудің комплекс түбірлері.  болғандықтан, жалпы шешімі мына түрде болады:
болғандықтан, жалпы шешімі мына түрде болады: 
Жауабы:  .
.
Тапсырма 11. Коэффициенттері тұрақты сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімін табыңыз:

Шешуі.
Бұл екінші ретті коэффициенттері тұрақты сызықтық біртекті емес дифференциалдық теңдеу:
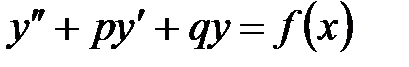 , мұндағы
, мұндағы 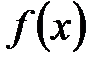
 .
.
Жалпы шешімін мына түрде іздейміз:  =
=  бірт. +
бірт. +  д.ш.,
д.ш.,
мұндағы  бірт. – берілген теңдеуге сәйкес біртекті теңдеудің жалпы шешімі,
бірт. – берілген теңдеуге сәйкес біртекті теңдеудің жалпы шешімі,  д.ш. =
д.ш. = 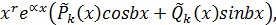 мұндағы
мұндағы 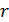
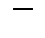 cипаттаушы теңдеудің түбірлерінің ішіндегі a+bi
cипаттаушы теңдеудің түбірлерінің ішіндегі a+bi 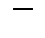 дің саны,
дің саны, 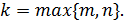 .
.
1) Берілген теңдеуге сәйкес біртекті теңдеуін жазып, жалпы шешімін табамыз:  ,
,  cипаттаушы теңдеуі,
cипаттаушы теңдеуі,  cипаттаушы теңдеудің түбірлері, демек
cипаттаушы теңдеудің түбірлері, демек  бірт.
бірт.  .
.
2) Біртекті емес теңдеудің дербес шешімін  функциясының түріне байланысты анықталмаған коэффициенттер тәсілімен табамыз:
функциясының түріне байланысты анықталмаған коэффициенттер тәсілімен табамыз:  және
және  cипаттаушы теңдеудің түбірі болмайтындықтан, дербес шешімді
cипаттаушы теңдеудің түбірі болмайтындықтан, дербес шешімді 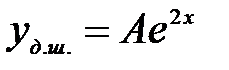 түрінде іздейміз. Сонда
түрінде іздейміз. Сонда 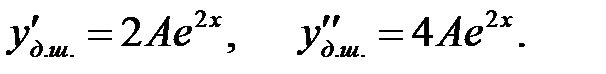 Белгісіз
Белгісіз  коэффициентті табу үшін
коэффициентті табу үшін 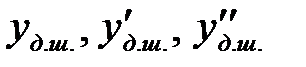 мәндерін бастапқы теңдеуге қоямыз:
мәндерін бастапқы теңдеуге қоямыз:
 ,
,  .
.
Демек, 
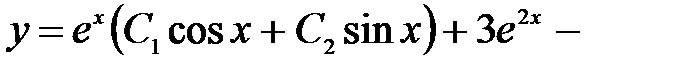 жалпы шешімі.
жалпы шешімі.
Жауабы:  .
.
Тапсырма 12. Дифференциалдық теңдеулер жүйесін айнымалыны жою тәсілімен шешіңіз:

Шешуі.
Бірінші теңдеуді  бойынша дифференциалдаймыз:
бойынша дифференциалдаймыз:  . Жүйеден
. Жүйеден 
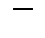 ті жою үшін екі теңдеуді қосамыз:
ті жою үшін екі теңдеуді қосамыз:  . Демек,
. Демек, 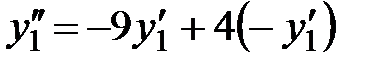 ;
;  коэффициенттері тұрақты сызықтық біртекті дифференциалдық теңдеу.
коэффициенттері тұрақты сызықтық біртекті дифференциалдық теңдеу.

 ,
,  .
.  – ні бірінші теңдеуден табамыз:
– ні бірінші теңдеуден табамыз: 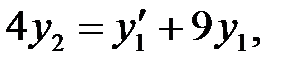

Жауабы: 
Дебиеттер
1. Хасеинов К.А. Математика канондары. – Алматы: MMIV, 2004.
2. Ибрашев Х.И., Еркеғұлов Ш.Т. Математикалық анализ курсы.
1,2 т. Алматы: 1963–1970.
3. Көксалов К.К. Жоғары математика курсы. – Алматы: 2002.
4. Айдос Е.Ж. Жоғары математика.–Алматы: «Иль-Тех-Кітап», 2003.
5. Шипачев В.С. Высшая математика. – М.: В Ш, 1985. –369 с.
6. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т.1,2 – М.: Наука, 1985. – 432 с.
7. Данко П.Е., и др. Высшая математика в упражнениях и задачах. ч.1,2. 2003.
8. Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа /Под ред. А.В. Ефимова и Б.П. Демидовича. – М.: Наука, 1986, 2002– 368 с.
9. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). – М.: Высшая школа, 1983. –176 с.
10. Базарбаева С.Е., Ким Л.Н., Курбанова Р.А. Математика 3 (методические указания и тестовые задания для подготовки к экзамену).-Алматы: АИЭС,-2007.-27 с.
11. Индивидуальные задания по высшей математике: Комплексные числа. Неопределенные и определенные интегралы. Функции нескольких переменных. Обыкновенные дифференциальные уравнения ч.2: Учеб. пособие/ под ред. А.П. Рябушко – Мн.:Выш.шк.,2000.-396 с.
12. Жуматаева С.А.,Темешева С.М. Математика 3. Конспект лекций (для студентов всех форм обучения всех специальностей).- Алматы: АИЭС, -2008.- 66 с.
13. Базарбаева С.Е., Дулэпо В.М. Высшая математика. Методические указания и задания к расчетно графической работе. Ч.6. – Алматы: АИЭС, 2002 – 32 с.
Мазмұны
| 1. | Кіріспе | |
| 2. | Есептеу –сызба жұмыстарының тапсырмалары | |
| 3. | Тапсырмаларды орындауға әдістемелік нұсқаулар. Типтік нұсқаның шешуі | |
| 4. | Әдебиеттер тізімі |






