Жидкая частица в противоположность твердой при движении может изменять форму, т.е. деформироваться. Поэтому, в общем случае движение жидкой частицы может быть разложено на поступательное, вращательное и деформационное.
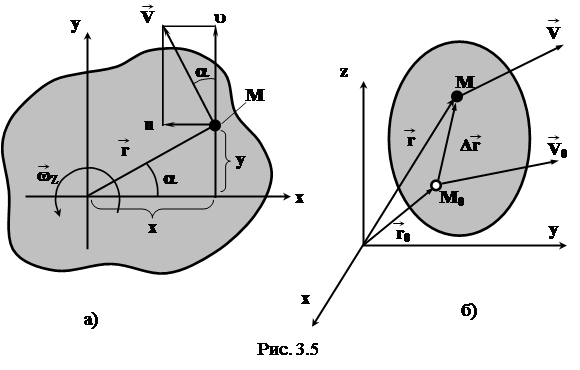
Рассмотрим движение точки 
(рис. 3.5) твердого тела, вращающегося вокруг оси Z с угловой скоростью 
и запишем уравнения составляющих скорости точки М:
u = - wz r∙sina = - wz y, (3.58)
u = wz r∙cosa = wz x. (3.59)
 |
Дифференцируя эти уравнения, получаем следующие выражения
. (3.60)
Суммируя левые и правые части этих выражений, получаем
 |
. (3.61)
Тогда:
. (3.62)
По аналогии с полученным выражением, можем записать:
, (3.63)
. (3.64)
Связь между скоростями V и V0 двух произвольных точек твердого тела (рис. 3.5б) выражается соотношением
, (3.65)
где 
.
Выберем в жидкой частице точки М и М0 достаточно близкими и разложим в ряд Тейлора мгновенные значения проекций скорости u, u, w в точке М, ограничиваясь линейными членами ряда.
Для компоненты u имеем
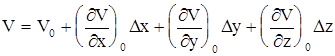, (3.66)
где Dx, Dy, Dz - проекции вектора 
, а индексом «0» отмечены значения производных в точке М0.
Используя тождества
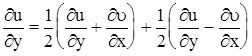; (3.67)
, (3.68)
 |
запишем выражение для ux в виде
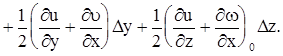(3.69)
Для двух других компонент по аналогии можно получить
; (3.70)
. (3.71)
Анализируя полученные формулы, можно сделать вывод о том, что вторые и третьи члены в правой части записанных выражений образуют проекции векторного произведения некоторого вектора 
на радиус-вектор , причем проекциями вектора служат выражения
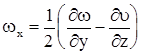; (3.72)
; (3.73)
. (3.74)
Это позволяет считать, что жидкая частица, также как и твердое тело, испытывает вращение с угловой скоростью 
относительно некоторой мгновенной оси.
В гидромеханике, наряду с вектором 
, вращательное движение частиц характеризуют вектором 
, который называется вихрем или ротором вектора 
.
 |
Очевидно, что в записанных формулах для проекций скорости жидкой частицы можно выделить проекции скорости квазитвердого движения 
.
, (3.75)
где 
, и в этом случае имеет место компонента uдеф - скорость, обусловленная деформацией жидкой частицы.
Для выяснения смысла вектора 
рассмотрим некоторые частные случаи движения частицы жидкости (рис. 3.6).
 |
Пусть малый жидкий отрезок Dх движется вдоль оси Х. Скорость левого конца составляет u, а скорость правого конца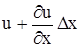 
. Вследствие разницы в этих скоростях за время Dt длина отрезка изменится на величину 
. Скорость изменения длины будет равна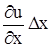 
и, соответственно, по аналогии имеем: 
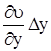и 
, представляющие собой скорости удлинения элементарных отрезков Dy и Dz.
Производные
; 
; 
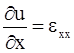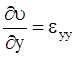являются скоростями удельных линейных деформаций или скоростями удлинения отрезков единичной длины.
При рассмотрении движения жидкого отрезка Dx вдоль оси у можно сделать вывод о том, что вследствие неодинаковости скоростей отрезок Dx за время Dt переместится и повернется на угол
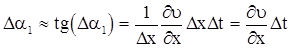. (3.76)
Угловая скорость его вращения будет 
. По аналогии угловая скорость вращения отрезка Dy будет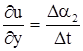 
. Вследствие вращения отрезков Dx и Dy, образовавших вначале прямой угол, произойдет угловая деформация в плоскости «ху». Скорость угловой деформации определится суммой углов Da1 и Da2 и будет равна 
.
В гидродинамике за меру скорости угловой деформации принимают половину этой величины.
; (3.77)
; (3.78)
. (3.79)
Формулы для проекций скоростей жидкой частицы с учетом полученных выше соотношений запишутся в виде:
u = u0 + wyDz - wzDy + exxDx +exyDy + exzDz; (3.80)
u = u0 + wzDx - wxDz + eyxDx +eyyDy + eyzDz; (3.81)
w = w0 + wxDy - wyDx + ezxDx +ezyDy + ezzDz. (3.82)
Записанные формулы выражают в теорему Коши-Гельмгольца: в общем случае движение жидкой частицы можно разложить на переносное движение с некоторым полюсом, вращательное движение с угловой скоростью 
вокруг мгновенной оси, проходящей через этот полюс, а также деформационное движение, которое заключается в линейных деформациях со скоростями exx, eyy, ezz и угловых деформациях со скоростями exy = eyx, exz = ezx, eyz = ezy.
В частных случаях некоторые из составляющих движения могут отсутствовать.
