Третья аксиома. Сила инерции

 

При действии одного тела на другое возникают две силы, равные по величине, направленные по одной прямой в противоположные стороны и приложенные к телам в точке касания.

Конечно, нельзя сказать, что эти две силы уравновешиваются, так как они приложены к разным телам.

Проведём небольшой эксперимент. Попробуем перемещать тяжёлое тело по некоторой криволинейной траектории. Сразу обнаружим, что тело сопротивляется изменению направления движения, изменению скорости. Возникает сила со стороны тела, противодействующая силе 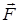, той, которую мы прикладываем к нему.

Эту силу, с которой материальная точка сопротивляется изменению своего движения, будем называть силой инерции этой точки - 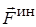. По третьей аксиоме она равна и противоположна действующей на точку силе 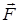, . Но на основании второй аксиомы . Поэтому .

Итак, сила инерции материальной точки по величине равна произведению её массы на ускорение

. (12.2.)

И направлена эта сила инерции в сторону противоположную вектору ускорения.

Например, при движении точки по кривой линии ускорение . Поэтому сила инерции

.

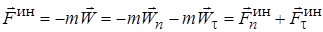То есть её можно находить как сумму двух сил: нормальной силы инерции и касательной силы инерции (рис. 12.1). Причём

Рис. 12.1.

Необходимо заметить, что сила инерции материальной точки, как сила противодействия, приложена не к точке, а к тому телу, которое изменяет её движение. Это очень важно помнить.

 

XIII. Динамика материальной точки

 

Исследование движения тел начнём с анализа движения материальной точки. При этом приходится решать две задачи. Первая задача – известно как точка движется, нужно определить силы вызывающие это движение; вторая, обратная задача – известны силы, действующие на точку, определить как она будет двигаться.

 

 

Первая задача обычно решается методом кинетостатистики.

Метод кинетостатистики

 

Пусть на точку действует несколько сил. Составим для неё основное уравнение динамики: 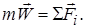Перенесём все члены в одну сторону уравнения и запишем так: или .

Это уравнение напоминает условие равновесия сходящихся сил. Поэтому можно сделать вывод, что, если к движущейся материальной точке приложить её силу инерции, то точка будет находиться в равновесии. (Вспомним, что на самом деле сила инерции не приложена к материальной точке и точка не находится в равновесии.) Отсюда следует метод решения таких задач, который называется методом кинетостатики:

 

Если к силам, действующим на точку, добавить ее силу инерции, то задачу можно решать методами статики, составлением уравнений равновесия.

Пример 13.1. При движении автомобиля с постоянным ускорением , маятник (материальная точка подвешенная на нити) отклоняется от вертикали на угол a (рис. 13.1). Определим с каким ускорением движется автомобиль и натяжение нити.

Рассмотрим «динамическое равновесие» точки. Его так называют потому, что на самом деле точка не находится в равновесии, она движется с ускорением.

На точку действуют силы: вес и натяжение нити , реакция нити. Приложим к точке ее силу инерции , направленную в сторону противоположную ускорению точки и автомобиля, и составим уравнение равновесия:

Рис. 13.1.

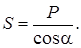Из второго уравнения следует Из первого 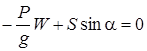и 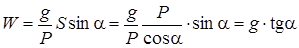.