ЛАБОРАТОРНАЯ РАБОТА №1
Формирование сигнала по заданному спектру с анализом влияния
Каждой гармоники.
ЦЕЛЬ РАБОТЫ.
Овладеть навыками построения спектра периодических сигналов, исследовать связь между формой периодического сигнала и его односторонним спектром.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Понятие измерительного сигнала.
В технических отраслях знаний термин "сигнал" (signal, от латинского signum – знак) очень часто используется в широком смысловом диапазоне, без соблюдения строгой терминологии. Под ним понимают и техническое средство для передачи, обращения и использования информации - электрический, магнитный, оптический сигнал; и физический процесс, представляющий собой материальное воплощение информационного сообщения - изменение какого-либо параметра носителя информации (напряжения, частоты, мощности электромагнитных колебаний, интенсивности светового потока и т.п.) во времени, в пространстве или в зависимости от изменения значений каких-либо других аргументов (независимых переменных); и смысловое содержание определенного физического состояния или процесса, как, например, сигналы светофора, звуковые предупреждающие сигналы и т.п. Все эти понятия объединяет конечное назначение сигналов. Это определенные сведения, сообщения, информация о каких-либо процессах, состояниях или физических величинах объектов материального мира, выраженные в форме, удобной для передачи, обработки, хранения и использования этих сведений.
Динамическое представление сигналов
При исследовании преобразования сигналов линейными цепями во многих случаях целесообразно пользоваться не временной, а частотной формой описания сигналов, а именно: представлять (изображать) сигналы в виде частотных спектров, то есть совокупностью гармонических колебаний (в кратком изложении — гармониками).
Спектральная (частотная) форма представления сигналов использует разложение сигнальных функций на периодические составляющие. Термин "spectrum" ("спектр") впервые применил И. Ньютон в 1571 году при описании разложения солнечного света, пропущенного через стеклянную призму, на многоцветную полосу. В 18-м веке уже Бернулли и Эйлер показали, что произвольные периодические функции представляют собой суммы простейших гармонических функций – синусов и косинусов кратных частот. Эти суммы получили название рядов Фурье, после того как в 1807 году французский инженер Жан Батист Фурье обосновал метод вычисления коэффициентов тригонометрического ряда, которым можно отображать с абсолютной точностью (при бесконечном числе членов ряда) или аппроксимировать с заданной точностью (при ограничении числа членов ряда) любую периодическую функцию, определенную на интервале одного периода T = b - a, и удовлетворяющую условиям Дирихле (ограниченная, кусочно-непрерывная, с конечным числом разрывов 1-го рода). Ряды Фурье в вещественной форме имеют следующий вид:
s(t) =(a0/2) + 
(an cos(2pnf1t) + bn sin(2pnf1t), f1 = 1/T.
an = (2/T)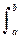 
s(t) cos(2pkf1t) dt, bn = (2/T) 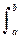s(t) sin(2pkf1t) dt.
На первых этапах своего развития данное направление разложения функций, получившее название гармонического анализа, имело больше теоретический характер и использовалось, в основном, в естественных науках для выявления и изучения периодичности и состава периодических составляющих (в том числе скрытых) в различных явлениях и процессах (активность солнца, метеорологические наблюдения, и т.п.). Положение резко изменилось с появлением электротехнических и радиотехнических отраслей науки и техники и развитием радиосвязи, где гармонический состав сигналов приобрел конкретный физический смысл, а математический аппарат спектрального преобразования функций стал основным инструментом анализа и синтеза сигналов и систем. Сейчас спектральный анализ является одним из основных методов обработки экспериментальных данных во многих отраслях науки и техники.
В качестве базисных функций разложения сигналов, в общем случае, принимаются комплексные экспоненциальные функции exp(j2pft), от которых с использованием формул Эйлера можно перейти к вещественным синус - косинусным функциям. Понятие частотного преобразования не следует связывать только с временными аргументами, т.к. математический аппарат преобразования не зависит от физического смысла независимых переменных. Так, например, при переменной " х ", как единице длины, значение f будет представлять собой пространственную частоту с размерностью 1/|х | - число периодических изменений сигнала на единице длины. В математическом аппарате частотного анализа удобно использовать угловую частоту w = 2pf.
Переход к частотным спектрам позволяет согласовать способы описания сигнала и цепи, для которой известна частотная характеристика, а именно: комплексный коэффициент передачи, или передаточная функция. Поскольку любое реальное колебание или произвольный сигнал можно представить совокупностью гармонических колебаний, выявление формы сигнала на выходе линейной цепи сводится к анализу прохождения через цепь каждой гармоники по отдельности. Согласно принципу суперпозиции, отклик цепи на отдельную гармонику не будет зависеть от присутствия в спектре сигнала остальных гармонических составляющих. Если известна реакция цепи на гармоническое колебание произвольной частоты, суммируя (интегрируя) результат воздействия многих гармоник, можно вернуться к временному представлению сигнала на выходе цепи и таким образом выяснить, как данная цепь изменит заданный сигнал. Эта схема исследования составляет суть спектрального анализа. Умение оперировать спектрами позволяет во многих случаях выявлять изменение формы сигналов, не прибегая к сложным вычислениям.
