МЕТОДЫ СТАТИСТИЧЕСКОГО АНАЛИЗА ДАННЫХ В ЭМПИРИЧЕСКОМ ИССЛЕДОВАНИИ
АНАЛИЗ ПАРНОГО РАСПРЕДЕЛЕНИЯ ПРИЗНАКОВ
Парное (двухмерное) распределение признаков — это распределение совокупности по двум переменным. Если переменная № 1 влияет на переменную №2, то первую называют независимой переменной, а вторую — зависимой. 1
В исследовательской практике нередки случаи, когда нельзя точно определить, какая именно переменная оказывает влияние, а какая — объект воздействия. Например, что считать независимой переменной — оценку собственного здоровья или оценку политической ситуации в стране? В таких случаях лучше говорить о взаимо зависимости признаков.
Анализ двухмерных и трёхмерных распределений признаков, измеренных с помощью номинальных и порядковых шкал, осуществляется чаще всего на основе данных, полученных из таблиц двухмерного (парного) распределения. Эти таблицы нередко называют таблицами сопряжённости. В основе таблицы двухмерного распределения лежат два признака. Приведём пример простейшей таблицы парного распределения, основанной на двух номинальных признаках.
Таблица 2
Влияние участия в последних выборах на характер потребительского намерения
| Намерение купить | ||||
| Товар марки А | Товар марки В | Товар марки С | ||
| Имеет детей в возрасте до 16 лет | 27, 2% | 25,2% | 47,6% | 100,0% |
| Не имеет | 36,8% | 34,5% | 28,7% | 100,0% |
Из двух переменных – наличия детей и характера покупательского намерения — независимой переменной является наличие детей. Естественно, что именно оно может оказать влияние на намерение купить товар.
Для конструирования и описания таблицы следует:
1. Разделить респондентов на подгруппы, имеющие различные значения независимой переменной
2. Сравнить выделенные подгруппы при помощи процентов лиц, имеющих определенные значения зависимой переменной
Наличие детей является независимой переменной, поэтому массив был разделен на подгруппы имеющих и не имеющих детей. Соответственно за 100% берётся численность респондентов, имеющих значения независимой переменной — “имеет” и “не имеет”.
Описать данную таблицу мы можем, сравнив группы имеющих и не имеющих детей при помощи процентов лиц, обладающих определенным значением зависимой переменной. В нашем случае это намерение купить товар определённой марки. Однако, описывать таблицу сопряженности мы имеем право лишь после расчёта значения определённого статистического критерия.
Статистический анализ таблицы сопряжённости двух номинальных признаков
Приведём пример статистического анализа взаимосвязи двух номинальных признаков: участия в последних выборах и потребительских предпочтений.
Для того, чтобы ответить на вопрос, существует ли взаимосвязь между наличием детей и характером покупательского намерения, следует проанализировать таблицу сопряжённости данных двух признаков, применив статистический критерий.
Статистический критерий – правило, при помощи которого проверяются статистические гипотезы. Нулевая гипотеза в данном случае — предположение о статистической независимости рассматриваемых переменных, то есть наличие детей не влияет на характер потребительских намерений. Альтернативная гипотеза —предположение о том, что указанные переменные взаимозависимы, их связь является статистически значимой.
Корреляционная связь является значимой, когда с высокой степенью уверенности можно утверждать, что она вызвана не случайными причинами – колебаниями выборочных показателей вокруг генерального — а наличием такой связи в генеральной совокупности. Нужно отметить, что наличие корреляционной связи необязательно означает существование причинно-следственной связи между данными признаками. Эта связь может быть следствием некой третьей причины, также оба признака могут выступать и в качестве причины, и следствия.
Доверительная вероятность Р —вероятность правильности альтернативной гипотезы. Величина, связанная с доверительной вероятностью — уровень значимости 
, он равен 1-Р. Это вероятность ошибки в нашем выводе о подтверждении альтернативной гипотезы. Если, например, Р=0,95, то =1-0,95=0,05.
Применим для проверки нулевой гипотезы статистический критерий 
,он применяется для анализа взаимосвязей, прежде всего номинальных признаков. В случае, если расчётное значение критерия превысит его критическое значение, определяемое по таблицам распределения ,нулевая гипотеза отвергается. Нужно отметить, что расчёты для определения значимости корреляционной связи осуществляют, основываясь на постулате, что выборка была простой случайной.
Таблица 3
Расчётное значение (основа расчётов – таблица 2)
| Критерий
| Значение |
| 70,39 |
Приемлемым для общественных наук является уровень значимости, равный 0,05 и меньше, то есть вероятность ошибки пять шансов из ста. Если исследователь получает в процессе машинной обработки данных информацию именно о таком уровне значимости, то он может с полным основанием формулировать вывод о наличии связи между признаками. Если же уровень значимости оказался равным величине, большей 0,05, например, составил 0,07, то делать заключение такого рода нельзя.
Формула расчёта числа степеней свободы для таблицы сопряженности имеет следующий вид: df=(c-1)(r-1), где с-число столбцов, r-число строк таблицы. Для нашего случая с=3; r=2, поэтому df=(3-1)(2-1)=2.
Определив число степеней свободы и задав уровень значимости, равный 0,05, мы можем определить критическое значение данного критерия по специальным таблицам.
Приведём фрагмент таблицы «Значения - критерия Пирсона» для уровня значимости 0,05.
| df(число степеней свободы) | |||||
| 3,84 | 5,99 | 7,81 | 9,49 | 11,07 |
Как видно из таблицы, критическое значение для двух степеней свободы составляет 5,99, расчётное же значение критерия – 70,39.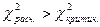 
. То есть расчётное значение критерия превышает критическое. Следовательно, статистическая связь между наличием детей и характером потребительских намерений является значимой.
Описывая таблицу 2, исследователь должен указать, что покупательские предпочтения различаются в группах людей, имеющих и не имеющих детей. Следует отметить, что наиболее существенно группы, имеющие и не имеющие детей, отличаются по доле приверженцев марки С. Среди имеющих детей эту марку выбрали 47,6%, а среди не имеющих — всего 28,7% (см. табл. 2). Если в первой группе товар марки С стоит на первом месте по “популярности”, то во второй группе — на третьем.
Убедившись в том, что связь между исследуемыми переменными является статистически значимой, можно определить её силу (тесноту).
Коэффициент корреляции является мерой зависимости между признаками. Его численное значение и знак указывают на силу (тесноту) и направление корреляционной связи. Численное значение коэффициента корреляции указывает на тесноту связи и может по модулю меняться от нуля до единицы. Чем ближе значение коэффициента к единице, тем связь сильнее. Будем считать связь тесной (сильной), если значение коэффициента корреляции составляет 0,7 и более. Если коэффициент равен 0,3-0,699, то связь умеренная. Значения менее 0,3 указывают на слабую связь.
Довольно часто для анализа тесноты взаимосвязи двух номинальных признаков применяется коэффициент корреляции Крамера. Он изменяется от 0 до 1 и указывает только на тесноту, а не направление связи. Поэтому данный коэффициент не может иметь отрицательных значений. Коэффициент Крамера считается значимым, если эмпирическое значение критерия , рассчитанное для таблицы, окажется больше критического, то есть в том случае, если связь между признаками, положенными в основу таблицы, будет статистически значимой (то есть она существует не только в выборке, но и в генеральной совокупности).
(2)
N — объём выборки; r—число строк; k—число столбцов в таблице; число строк в таблице №2 равно двум, число столбцов – трём.
Min (r-1, k-1) — минимальная из двух величин r-1 и k-1. В нашем случае минимальным из чисел, равных 2-1 и 3-1 является 2-1=1.
К= 
Так как значение коэффициента составляет менее 0,3, то связь между анализируемыми признаками является слабой. Однако, она статистически значима; значимость мы уже проверили с помощью критерия (см. табл.3)
