Статистический анализ уравнения регрессии начинается с проверки адекватности полученного уравнения приближенной регрессии результатам эксперимента. В общем случае гипотеза об адекватности должна быть принята, если выполняется условие
(11)
где 
– табличное значение критерия Фишера при уровне значимости 
и числа степеней свободы числителя 
и 
;
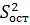- остаточная дисперсия, обусловленная влиянием неучтенных факторов и ошибками измерений в ходе проведения эксперимента;
- дисперсия воспроизводимости, характеризующая рассеивание значений выходного параметра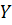 
при повторении одного и того же опыта, при одном и том же сочетании уровней факторов.
Однако, при выполнении пассивного эксперимента, вследствие трудности повторения опытов при неизменных условиях функционирования системы, получение дисперсии воспроизводимости становится практически невозможным.
В рассматриваемых условиях для проверки адекватности целесообразно воспользоваться эмпирической зависимостью
(12)
где 
- оценка дисперсии выходного параметра ;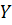
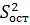- остаточная дисперсия.
Оценки дисперсии рассчитываются по следующим формулам:
(13)
(14)
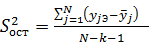(15)
где 
- оценка выходного параметра, вычисленная для j-го опыта по заданному уравнению регрессии.
Если условие (12) выполняется, то гипотезу об адекватности полученного уравнения приближенной регрессии результатам пассивного эксперимента следует принять. В противном случае, при неизменном составе входных факторов, следует выдвинуть конкурирующую гипотезу о нелинейном виде математической модели и весь процесс вычислений повторить для получения модели в виде неполного квадратного или полного квадратного полинома. Так, повышая постепенно степень полинома, можно получить в конечном итоге адекватную математическую модель.
После получения адекватной модели переходят ко второму этапу статистического анализа. На данном этапе производится селекция входных факторов, суть которой заключается в следующем. На величину входного параметра системы, как правило, существенно влияет лишь часть из всей совокупности 
включенных в фактор экспериментов. Для выявления незначимых факторов производится проверка значимости всех коэффициентов регрессии 
с помощью t -критерия Стьюдента.
Факторы, для которых выполняется условие
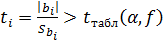(16)
где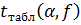 
- табличное значение критерия Стьюдента для уровня значимости и числа степеней свободы 
;
- оценка среднеквадратического отклонения i -го коэффициента регрессии.
являются значимыми, и их следует оставить в уравнении регрессии.
Процесс отбрасывания незначимых коэффициентов последовательно повторяется до тех пор, пока в адекватном уравнении останутся только значимые коэффициенты регрессии.
Задание
1. Задать 
выборок выходных параметров 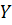с нормальным законом распределения объемом 8 значений (значение берется из таблицы согласно варианту).
2. Задать число входных факторов 
.
3. Выполнить проверку возможности проведения обработки результатов эксперимента методом множественного регрессионного анализа по критерию Кохрена.
4. Определить значения коэффициентов 
и записать уравнение приближенной регрессии в виде
5. Выполнить проверку адекватности уравнения регрессии результатам эксперимента. Если условие адекватности выполняется, то необходимо выполнить проверку значимости оценок коэффициентов регрессии.
6. Если условие адекватности не выполняется, следует расширить исходную матрицу планирования, изменив уравнение регрессии на неполноквадратичное.
7. Для неполного квадратичного уравнения определить значения коэффициентов, выполнить проверку адекватности уравнения регрессии результатам эксперимента и проверку значимости коэффициентов регрессии.
