Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.
Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:
§ 
§ 
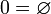
Числа, заданные таким образом, называются ординальными.
Первые несколько ординальных чисел и соответствующие им натуральные числа:
§
§ 
§ 
§ 
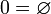
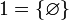
Операции над натуральными числами 
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
§ Сложение. Cлагаемое + Слагаемое = Сумма
§ Умножение. Множитель * Множитель = Произведение
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
§ Вычитание. Уменьшаемое 
Вычитаемое = Разность. При этом Уменьшаемое должно быть больше Вычитаемого (или равно ему, если считать 0 натуральным числом).
§ Деление. Делимое / Делитель = (Частное, Остаток). Частное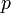 
и остаток 
от деления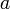 
на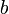 
определяются так: 
, причём 
. Заметим, что именно последнее условие запрещает деление на ноль, так как иначе 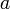можно представить в виде 
, т.е. можно было бы считать частным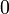 
, а остатком = .
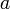Следует заметить, что именно операции сложения и умножения являются основополагающими. В частности, кольцо целых чисел определяется именно через бинарные операции сложения и умножения.
Основные свойства
1. Коммутативность сложения. 
2. Коммутативность умножения. 
3. Ассоциативность сложения. 
4. Ассоциативность умножения. 
5. Дистрибутивность умножения относительно сложения.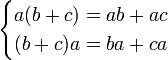 
Натуральные числа в русском языке
§ Числа от 1 до 10 — один (1), два (2), три (3), четы́ре (4), пять (5), шесть (6), семь (7), во́семь (8), де́вять (9), де́сять (10).
§ Числа от 11 до 20 — одиннадцать (11), двенадцать (12), тринадцать (13), четырнадцать (14), пятнадцать (15), шестнадцать (16), семнадцать (17), восемнадцать (18), девятнадцать (19), двадцать (20).
§ Числа от 30 до 90 — тридцать (30), сорок (40), пятьдесят (50), шестьдесят (60), семьдесят (70), восемьдесят (80), девяносто (90).
§ Числа от 100 до 900 — сто (100), двести (200), триста (300), четыреста (400), пятьсот (500), шестьсот (600), семьсот (700), восемьсот (800), девятьсот (900).
§ Большие числа — тысяча, миллион, миллиард, триллион.
§
§ Рациональные числа
§
§ Отрицательные числа.Целые отрицательные числа.
§ Дробные отрицательные числа. Положительные числа.
§ Рациональные числа.
§
§ Отрицательные числа появляются, когда из меньшего числа вычитают большее, например:
§
§ 10 – 15 = – 5.
§
§ Знак «минус» перед 5 показывает, что это число отрицательное.
§
Ряд целых отрицательных чисел бесконечен:
§
§ –1, –2, –3, – 4, –5,...
§
Целые числа - это натуральные числа, целые отрицательные числа и ноль:
§
§..., –3, –2, –1, 0, 1, 2, 3,...
§
§ Дробные отрицательные числа появляются, например, когда из меньшего дробного числа вычитают большее:
§ 
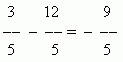
§ Можно также сказать, что дробные отрицательные числа появляются в результате деления целого отрицательного числа на натуральное:
§ 
§ Положительные числа (целые и дробные) в противоположность отрицательным числам (целым и дробным) рассматриваются в арифметике.
§
§ Рациональные числа – это положительные и отрицательные числа (целые и дробные) и ноль. Более точное определение рациональных чисел, принятое в математике, следующее:
§ Число называется рациональным, если оно может быть представлено в виде обыкновенной несократимой дроби вида: m / n, где m и n целые числа.
