Однофазные цепи синусоидального тока

Содержание

1.Краткие теоретические сведения

2. Задание на расчет

3. Примеры расчета цепи

4. Контрольные вопросы

 

1. Краткие теоретические сведения

Переменный электрический ток – это ток, изменяющийся с течением времени. Значение этой величины в рассматриваемый момент времени называется мгновенным значением тока i. Наиболее распространен переменный синусоидальный ток, являющийся синусоидальной функцией времени.

Переменный синусоидальный сигнал характеризуется:

· периодом Т, который выражается в секундах (с),

· частотой f - величиной, обратной периоду, выражается в герцах (Гц).

· круговой частотой ω = 2π f (1/с).

Мгновенное значение тока: i = I_m sin (ωt + ψ_i), где:

· i – мгновенное значение тока, А;

· I_m – амплитудное значение тока, А;

· (ωt + ψ_i) фаза, рад;

· ω – круговая (угловая) частота, 1рад/с;

· ψ_i – начальная фаза тока, рад;

· t – время, с.

Синусоидальные величины принято изображать графиками – временными диаграммами. На графике принято использовать в качестве аргумента произведение ωt, измеряемое в радианах. Периодом становится 2 радиан.

Рис.2.1. Временная диаграмма синусоидального тока

Аналогичным образом характеризуются синусоидальные напряжения и ЭДС. Разность начальных фаз двух синусоидальных величин одной и той же частоты называют сдвигом фаз. Сдвиг фаз между напряжением и током определяется вычитанием начальной фазы тока из начальной фазы напряжения: φ = ψ_u – ψ_i

Действующее значение переменного тока – это среднеквадратичное значение переменного тока за период Т: I=Im/ .

Активными элементами цепи являются источники синусоидального напряжения одной и той же частоты ω. Пассивными элементами являются сопротивление, индуктивность и емкость.

Резистивный элемент - сопротивление характеризуется пропорциональностью между током и напряжением.

i = u/R = (Um/R) sin ωt = Im sin ωt

Резистивный элемент является потребителем электрической энергии.

В любой момент времени напряжение и ток совпадают по фазе, т.е. φ=0, а их амплитудные значения подчиняются закону Ома: U _{R m}=R I_m. Величина R – называется (активным) сопротивлением

Индуктивный элемент – индуктивность характеризуется напряжением самоиндукции.

u = L (di/d t) = ωL Im cos ωt = Um sin (ωt+π/2)

Индуктивный элемент накапливает магнитную энергию в виде магнитных силовых линий. Для амплитуд выполняется закон Ома:

U_Lm=ωL I_m. Величина Х_L =ωL – называется индуктивным сопротивлением, измеряется в Омах. Напряжение на индуктивном элементе по фазе опережает ток на угол φ= π/2.

Емкостной элемент - емкость характеризуется током смещения

i=Imsin ωt =C(duC/dt)= -ωС Uсm cos ωt = = UСm sin (ωt-π/2)

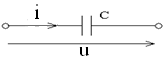
Емкостный элемент накапливает электрическую энергию в виде электрических силовых линий. Для амплитуд выполняется закон Ома:

I_m=ωС U_Сm. Величина Хс=1/ωC называется емкостным сопротивлением, измеряется в Омах. Напряжение на емкостном элементе по фазе отстает от тока на угол 90 градусов, φ= - π/2.

Неразветвленная цепь переменного тока с резистивным, индуктивным и емкостным элементами

 

Значение напряжения на зажимах этой цепи равно сумме значений трех составляющих: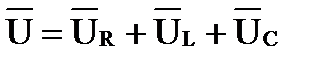

Действующее значение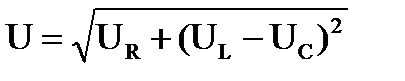

 

Сдвиг фаз между напряжением и током:

Х=X_L-X_C – реактивное сопротивление

- полное сопротивление цепи

Мощности цепи

Активная мощность, Вт:

P = U I cosφ = U_RI = I²R

Реактивная мощность, вар:

Q = U I sinφ = (U_L – U_C)I= I²X

Полная мощность, ВА:

S = U I = I²Z =

Цепь с параллельными ветвями

Рассмотрим разветвленную цепь, состоящую из двух ветвей.

Ток неразветвленной части цепи может быть определен по закону Ома: I = U/Z = UY, где Y-полная проводимость цепи.

Активная проводимость цепи G равна арифметической сумме активных проводимостей параллельных ветвей:

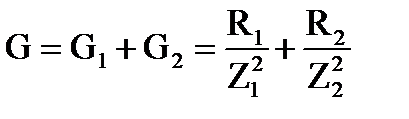
Реактивная проводимость цепи B равна разности индуктивных и емкостных проводимостей параллельных ветвей.

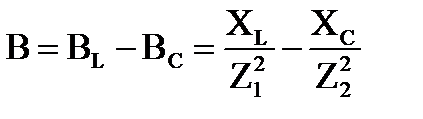
Компенсация реактивной мощности

Идея компенсации реактивной энергии индуктивного потребителя заключается в подключении к нему емкостного потребителя, в результате чего потребление реактивной энергии всей установкой уменьшается.

 

 

2. Задание

К однофазной цепи синусоидального тока напряжением U_н=220 В подключены потребители, типы и характеристики которых приведены в таблице.

Для светильников cos φ=1.

Составить эквивалентную схему замещения потребителей и определить параметры ее элементов.

Рассчитать емкость батареи конденсаторов, которую нужно подключить к потребителю для снижения реактивной мощности до нуля.

№ п/п	Однофазный трансформатор	Однофазный асинхронный двигатель	Светильники Рном, Вт х кол-во
тип	cos φ	тип	Рном, Вт	η, %	cos φ
	ОСМ-0,4	0,78	4ААЕ56В2			0,76	40x2
	ОСМ-0,063	0,75	АОЛБО 11-4			0,62	25x2
	ОСМ-0,25	0,85	4ААТ56А4			0,90	25x2
	ОСМ-0,1	0,75	АОЛБ012-4			0,62	40x2
	ОСМ-0,16	0,85	4ААЕ56А4			0,70	15x3
	ОСМ-0,063	0,75	АОЛБ11-4			0,62	25x2
	ОСМ-0,4	0,85	4ААТ56В4			0,90	40x2
	ОСМ-0,1	0,8	АОЛБ12-4			0,62	40x2
	ОСМ-0,1	0,85	4ААУ56В4			0,65	25x2
	ОСМ-0,25	0,75	АОЛБ21-4			0,62	60x2
	ОСМ-0.063	0,85	4ААТ50А2			0,80	15x3
	ОСМ-0,4	0,75	АОЛБ22-4			0,62	60x3
	ОСМ-0,16	0,82	4ААЕ50А2			0,68	15x2
	ОСМ-0,63	0,75	АОЛБ31-4			0,62	40x4
	ОСМ-0,25	0,8	4ААТ50В2			0,9	40x2
	ОСМ-1,0	0,75	АОЛБ32-4			0,62	200x2
	ОСМ-0,16	0.8	4ААЕ50В2			0,59	25x2
	ОСМ-0,063	0,78	АО Л Б011 -2			0,68	15x2
	ОСМ-0,1	0,82	4ААТ50А4			0,67	15x3
	ОСМ-0,16	0,78	АОЛБ012-2			0,70	15x3
	ОСМ-0,063	0.82	4ААУ50А4			0,51	15x2
	ОСМ-0,1	0.78	АОЛБ11-2			0,72	25x3
	ОСМ-0,1	0.8	4ААТ50В4			0,82	25x2
	ОСМ-0,16	0,78	АОЛБ12-2			0,72	40x2
	ОСМ-0.063	0.8	4ААЕ50В4			0,54	15x2
	ОСМ-0,25	0,78	АОЛБ21-2			0,72	80x2
	ОСМ-1,0	0,78	АОЛБ32-2			0,72	100x5
	ОСМ-0,4	0,78	АОЛБ22-2			0,72	40x5
	ОСМ-0,63	0,78	АОЛБ31-2			0,72	100x3
	ОСМ-0,1	0,9	АВЕО42-4			0,90	15x2
	ОСМ-0,63	0,78	4ААТ56В2			0,94	60x2
	ОСМ-0.063	0,78	АВЕО41-4			0,90	15x2
	ОСМ-0,1	0,78	4ААУ56А2			0,82	25x2
	ОСМ-0,4	0,78	АВЕО72-2			0,95	100x3
	ОСМ-0,16	0,78	4ААТ56А2			0,95	15x5
	ОСМ-0,25	0,78	АВЕ071-2			0,95	60x3
	ОСМ-0,25	0,9	4ААУ63В4			0,65	40x4
	ОСМ-0,16	0,78	АВЕ062-2			0,96	40x3
	ОСМ-0,4	0,9	4ААТ63В4			0,90	60x3
	ОСМ-0,1	0,78	АВЕ061-2			0,95	25x3
	ОСМ-0,4	0,9	4ААЕ63А4			0,65	25x4
	ОСМ-0,25	0,85	АВЕ052-2			0,95	15x4
	ОСМ-0,4	0,75	4ААЕ63В2			0,75	80x2
	ОСМ-0,16	0,85	ABE051-2			0,90	25x2
	ОСМ-0,16	0,9	4ААТ63А4			0,90	60x2
	ОСМ-0,1	0,95	АВЕ042-2			0,90	15x2
	ОСМ-0,63	0,75	4ААТ63В2			0,95	100x3
	ОСМ-0,063	0,85	АВЕ041-2			0,90	15x2
	ОСМ-0,16	0,75	4ААЕ63А4			0,65	25x3
	ОСМ-0,63	0,85	4АХТ71А2			0,95	200x2
	ОСМ-0,25	0,75	4ААТ63А2			0,95	40x5
	ОСМ-0,4	0,8	4АХЕ71А2			0,74	100x3
	ОСМ-0,4	0,82	4АХЕ71В4			0,70	60x4
	ОСМ-1,0	0,8	4АХТ71В2			0,95	150x4
	ОСМ-1,0	0,82	4АХТ71В4			0,92	100x4
	ОСМ-0,63	0,8	4АХЕ71В2			0,83	150x3
	ОСМ-0,25	0,82	4АХЕ71А4			0,70	40x4
	ОСМ-0.4	0,8	4АХТ71А4			0,92	100x2
	ОСМ-0,4	0,85	4ААУ63В2			0,75	60x2
	ОСМ-0,1	0,82	АВЕ061-4			0,95	25x2
	ОСМ-0,1	0,85	4ААУ63А4			0,65	40x2
	ОСМ-0,063	0,9	АВЕ052-4			0,90	25x2
	ОСМ-0,25	0.85	4ААУТ63В4			0,90	80x2
	ОСМ-0,16	0,82	АВЕ062-4			0,95	25x4
	ОСМ-0,16	0,85	4ААЕ63В4			0,65	60x2
	ОСМ-0,25	0,82	АВЕ071-4			0,95	40x3
	ОСМ-0,1	0,75	4ААЕ56А2			0,82	25x2
	ОСМ-0,4	0,83	АВЕ072-4			0,95	60x3
	ОСМ-0,16	0,75	4ААУ56В2			0,76	40x2
	ОСМ-0,063	0,82	ДГ-0,07			0,54	15x3
	ОСМ-0,4	0,8	ДГ-2-0,2			0,71	40x4
	ОСМ-0,1	0,8	ДГ-0,115			0,63	40x2
	ОСМ-0,25	0,8	ДГ-2-0,18			0,63	40x3
	ОСМ-0,16	0,8	ДГ-2-0,14			0,65	60x2

 

3. Примеры расчета цепи

Задание:

К однофазной цепи синусоидального тока напряжением U_ном=220 В подключены потребители:

однофазный трансформатор ОСМ-0,16, cos φ = 0,8;

однофазный асинхронный двигатель ДГ-2-0,14, Р_ном=140Вт, η=66%,

cos φ=0,65;

светильники 60 Вт, 2 штуки.

Составить эквивалентную схему замещения потребителей и определить параметры ее элементов.

Рассчитать емкость батареи конденсаторов, которую нужно подключить к потребителю для снижения реактивной мощности до нуля.

А1. Составление эквивалентной схемы замещения потребителей

Схемы замещения трансформатора и двигателя представляют собой совокупности активного и индуктивного элементов, светильники являются активными элементами. Все потребители соединяются параллельно.

Рис.2. Полная схема замещения потребителей энергии

Для определения параметров схемы замещения рассматриваем каждую из параллельных ветвей цепи отдельно.

Расчет трансформатора:

Число 0,16 в маркировке трансформатора означает его полную мощность, выраженную в киловольтамперах, то есть:

S_тр=0,16 кВА =160 ВA P_тр=S_трcosφ_тр=128 Вт

ток I_тр=S_тр/U=160/220=0,727 A

сопротивления: Z_тр=U/I_тр=220/0,727=302,613 Ом

R_тр=P_тр/I_тр²=128/0,727²=242,182 Ом

индуктивность L_тр=Х_L/2πf=0,578 Гн

Расчет двигателя:

Сначала необходимо определить активную мощность, потребляемую двигателем из сети:

Р_дв=Р_ном/η_дв=140/0,66=212,121 Вт

полная мощность S_дв=P_дв/cosφ_дв=212,121/0,65=326,34 BA

ток I_дв=S_дв/U=326,34/220=1,483 A

сопротивления:

Z_дв=U/I_дв=220/1,483=148,348 Ом

R_дв=P_дв/I_дв²=212,121/1,483²=96,45 Ом

индуктивность L_дв=Х_Lдв/2πf=0,359 Гн

Расчет светильников

Так как мощность светильников одинакова, значит параметры светильников будут равны между собой:

токи

I₁=I₂=P_св/U=60/220=0,273 А

сопротивления

R₁=R₂=P_св/I²=60/0,273²=805,056 Ом

Свернем полную схему в эквивалентную, состоящую из активного и реактивного двухполюсников.

Определяем проводимости: активные: Gтр=Rтр/Zтр2=242,182/302,6132=0,002644 См Gдв=Rдв/Zдв2=96,45/148,3482= 0,004383 См G1=G2=1/R1=1/R2=1/805,056=0,001242 См Эквивалентная активная проводимость цепи: G=Gтр+Gдв+G1+G2=0,009511 См

Реактивные проводимости трансформатора и двигателя равны:

B_тр=X_Lтр/Z_тр²=181,446/302,613²=0,001981 См

B_дв=X_Lдв/Z_дв²=112,714/148,348²= 0,005122 См

Реактивные проводимости светильников равны: B₁=B₂=0

Эквивалентная реактивная проводимость всей цепи:

B=B_тр+B_дв=0,007103 См

Эквивалентная полная проводимость всей цепи:

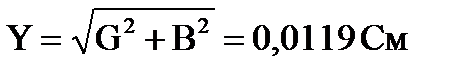
Определяем эквивалентные полное и активное сопротивления всей цепи, индуктивность, ток и активную мощность:

Z_экв=1/Y=1/0,0119=84,0336 Ом

R_экв=G/Y²=67,1633 Ом

X_Lэкв=B/Y²=50,1589 Ом

L_экв=X_Lэкв/2πf=0,1597 Гн

I_экв=U/Z_экв=2,618 А

Р=R_эквI_экв²=460,3322 Вт

Б. Подключим блок конденсаторов для снижения реактивной мощности

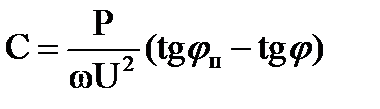Определяем tg φэкв исходной цепи: tg φэкв=XLэкв/Rэкв= 50,1589/67,1633=0,747 По условию задачи требуется обеспечить tg φ=0. Имеем для определения С=22,7 мкФ

 

Построим векторную диаграмму токов

Параметры диаграммы:

I_экв=2,618 А I_C=U/X_C=U·2πfC=1,17 A

φ_п=φ_экв=arctg(X_Lэкв/R_экв)=arctg 0,747=36,8° φ=0

Масштаб выбираем произвольно, например 1см = 0,5 А

Рис.3. Векторная диаграмма цепи после компенсации

Таким образом, при полной компенсации реактивной мощности

I=I_экв cos φ_пр= 2,096 A

Покажем построение графиков мгновенных значений тока и напряжения для эквивалентной схемы

I_экв=2,618 А

φ_п=36,8°

Мгновенные значения токов и напряжения определяются:

i = I_m sin (ωt + ψ_i)

u = U_m sin (ωt + ψ_u)

φ_п= ψ_u – ψ_i=36,8°

Примем ψ_u=0, тогда ψ_i=-36,8°= -(36,8°/180°)π =-0,204π радиан

i = 3,7024 sin (ωt -0,204π), u = 311,127 sin ωt

Рис.4. Временные диаграммы напряжения и тока в процентах от номинальной величины. В качестве номинальной величины приняты значения: для напряжения -300 В, для тока- 3 А.

Покажем построение графиков мгновенных значений для емкостного элемента

I_С=1,17 А

φ_С= - 90°

Мгновенные значения токов и напряжения определяются:

i = I_m sin (ωt + ψ_i)

u = U_m sin (ωt + ψ_u)

Примем ψ_u=0, тогда ψ_i= 90°= π/2 радиан

i = 1,65 sin (ωt +π/2), u = 311,127 sin ωt

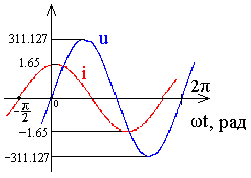
Построение графиков мгновенных значений входного напряжения и тока

I=2,096 A

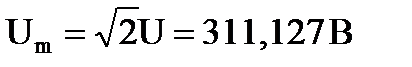
i = 2,964 sin ωt, u = 311,127 sin ωt

 

Проверка 1.

По условию задания и в результате расчета имеем

Sтр =160 ВА	cos φтр= 0,8	sinφтр=0,6
Sдв=326,3 ВА	cos дв= 0,65	sinφдв=0,76
U= 220 В	ω= 314 р/c	C = 22,7 10-6 Ф

 

Уравнение баланса реактивных мощностей можно записать следующим образом: Q_тр + Q_дв + Q_С =0, т.е.

S_тр sinφ_тр + S_дв sinφ_дв - ω С U² =0 или

160 0,6 +326,3 0,76 - 314 22,7 10^-6 220² =96+247- 344= -1.

Величина отклонения от нуля равна 1, что значительно меньше по величине любого из слагаемых, стоящих в левой части уравнения. Поэтому можно считать, что уравнение баланса реактивных мощностей выполняется.

Проверка 2.

Нами была смоделирована цепь согласно заданию, см. рис.4.

Рис.5. Проверка расчета путем моделирования цепи в программе EWB

Рис.6. Осциллограммы напряжения (VA1) и тока (VB2) в цепи после компенсации реактивной мощности

Из рис.6 видно, что ток и напряжение совпали по фазе, т.е расчет был проведен правильно.

 

Контрольные вопросы

1. Каковы фазовые соотношения между током и напряжением для идеализированных элементов:

· резистора;

· индуктивной катушки;

· конденсатора.

2.Как меняются фазовые соотношения между током и напряжением при переходе к пассивным реальным элементам, характеризуемым добротностью Q?

Резистор Катушка индуктивности 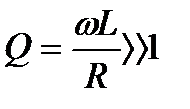Конденсатор

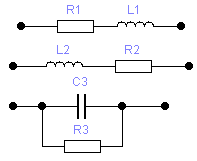
2. Как по показаниям амперметра, вольтметра и ваттметра определить параметры схем замещения реальных пассивных элементов цепи синусоидального тока?

3. Какова методика построения векторных диаграмм напряжений и токов в однофазных цепях?

4. Как можно определить активную и реактивную проводимости реальной индуктивной катушки?

5. Как можно определить активную, реактивную и полную проводимости исследуемой цепи?

6. Как применяются закон Ома и законы Кирхгофа для расчета разветвленных однофазных цепей?

7. Каковы условия наступления резонанса токов?

8. Что понимается под активной, реактивной и полной мощностью цепи?

9. Как рассчитывается коэффициент мощности и каково его технико-экономическое значение?

10. Как можно определить добротность параллельного резонансного контура?