Различные формы представления комплексного числа
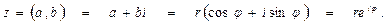
 | |||||||
 | |||||||
 | |||||||
 | |||||||
упорядоченная алгебраическая тригонометрическая показательная
пара форма форма форма
 модуль комплексного числа;
модуль комплексного числа;
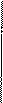
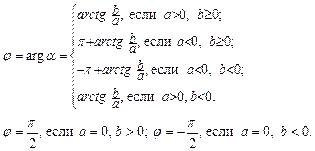
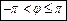
 – главное значение аргумента комплексного числа.
– главное значение аргумента комплексного числа.
Действия над комплексными числами
В тригонометрической и показательной формах
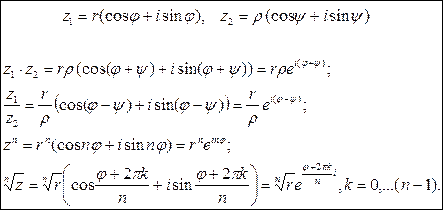
Уравнение окружности с центром в точке 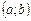
и радиусом 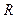
1) В декартовых координатах: 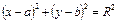 .
.
2) В комплексной форме: 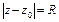 , где
, где  .
.
3) В параметрической форме: 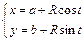 , где
, где  .
.
4) В комплексно-параметрической форме:
Так как 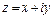 , то из 3)
, то из 3) 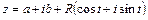 , где
, где  .
.
5) В показательной форме: 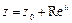 или
или 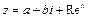 , где
, где  .
.
Элементарные функции в комплексной области
 , где
, где 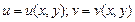 .
.
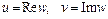 .
.
Показательная функция

 .
.
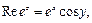
 .
.
Тригонометрические функции
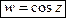
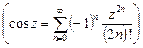 .
.
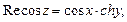
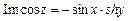 .
.
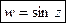
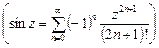 .
.
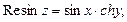
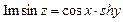 .
.
Связь между показательной и тригонометрическими
Функциями комплексного переменного
 – формула Эйлера.
– формула Эйлера.
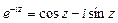 .
.
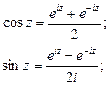
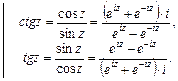
Гиперболические функции
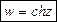
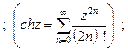

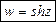


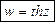
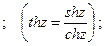
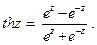
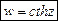
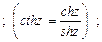
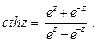
Обратные тригонометрические функции
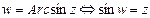

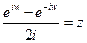 или
или 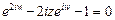 .
.
Решая это уравнение относительно 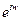 , получаем:
, получаем:
 Отсюда имеем:
Отсюда имеем:
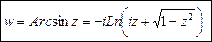
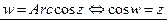
Решая уравнение  , получаем:
, получаем:
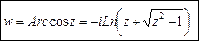
Аналогично получаем:
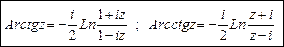
Логарифмическая функция
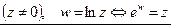
 ;
; 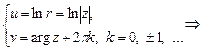

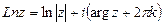 , где
, где 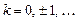

 .
.
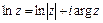 – главное значение логарифма.
– главное значение логарифма.
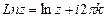 , где
, где 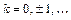
Свойства логарифмической функции
1) 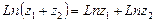 .
.
Следствие:  .
.
2)  .
.
Следствие: 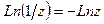 .
.
3)  .
.
Обобщенная степенная функция
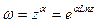 .
.
Дифференцируемость и аналитичность функции
Необходимые условия дифференцируемости
Если функция 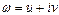 дифференцируема в точке
дифференцируема в точке 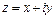 , то
, то  и
и  в точке
в точке  удовлетворяют условиям Коши-Римана
удовлетворяют условиям Коши-Римана
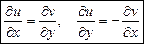
Достаточные условия дифференцируемости
Если функции 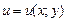 и
и 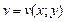 дифференцируемы в точке
дифференцируемы в точке  и удовлетворяет условиям Коши-Римана, то функция
и удовлетворяет условиям Коши-Римана, то функция  дифференцируема в точке
дифференцируема в точке  .
.
3) Формулы для вычисления производной функции 
а) 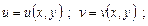
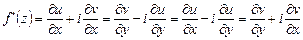 .
.
б) 
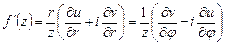 .
.
4) Если функция 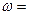
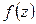 дифференцируема в каждой точке области и имеет в области непрерывную производную
дифференцируема в каждой точке области и имеет в области непрерывную производную 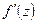 , то она называется аналитической в области.
, то она называется аналитической в области.
Ряды в комплексной области
Числовые ряды в комплексной области
 ;
;
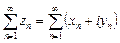 ; (
; (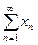 и
и 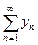 – числовые ряды).
– числовые ряды).
Теорема 1. Для того чтобы 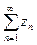 сходился и имел сумму
сходился и имел сумму  , необходимо и достаточно, чтобы ряды
, необходимо и достаточно, чтобы ряды 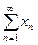 и
и  сходились и имели соответственно суммами числа
сходились и имели соответственно суммами числа 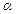 и
и 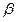 .
.
Теорема 2. Если 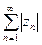 сходится, то сходится и ряд
сходится, то сходится и ряд 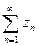 .
.
(Ряд 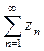 – абсолютно сходящийся ряд).
– абсолютно сходящийся ряд).
Справочные сведения о числовых рядах
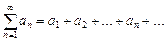 , (1)
, (1)
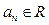 .
.
Необходимый признак сходимости:
Ряд (1) сходится => 
|
Вывод:
 => Ряд (1) расходится => Ряд (1) расходится
|
I. Знакоположительные ряды
 ,
, 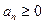
| Признак сравнения I | Признак сравнения II | ||
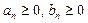 .
(1) .
(1) 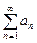 – миноранта,
(2) – миноранта,
(2) 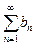 – мажоранта. – мажоранта.
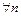 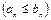 (3)
Ряд (2) сходится =>
Ряд (1) сходится.
Ряд(1) расходится =>
Ряд (2) расходится. (3)
Ряд (2) сходится =>
Ряд (1) сходится.
Ряд(1) расходится =>
Ряд (2) расходится.
|

(2)
Ряды (1) и (2) одновременно сходятся или расходятся. |
II. «Эталонные» ряды к признаку сравнения
| Геометрический ряд | Обобщенный гармонический ряд | ||
|
|
| Признак Даламбера |
(1) 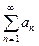 , , 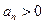
 => ряд (1) сходится, => ряд (1) сходится,

    => ряд (1) расходится, => ряд (1) расходится,
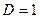 =>? =>?
|
| Радикальный признак Коши |
(1) 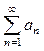 , , 
 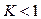 => ряд (1) сходится, => ряд (1) сходится,
  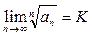  => ряд (1) расходится, => ряд (1) расходится,
 =>? =>?
|
Интегральный признак Коши
(1) 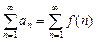 , , 
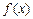 – непрерывная, неотрицательная, убывающая функция на
промежутке – непрерывная, неотрицательная, убывающая функция на
промежутке 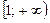 . Тогда . Тогда
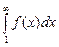 сходится => ряд (1) сходится, сходится => ряд (1) сходится,
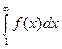 расходится => ряд (1) расходится. расходится => ряд (1) расходится.
|







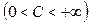
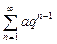 (1)
(1)
 => Ряд (1) сходится:
=> Ряд (1) сходится: 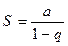 .
. => Ряд (1) расходится.
=> Ряд (1) расходится.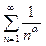 (2)
(2)
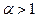 => Ряд (2) сходится;
=> Ряд (2) сходится; => Ряд (2) расходится.
=> Ряд (2) расходится.
