Задание. Написать первые четыре члена последовательности { xn }, если: 1) 
; 2) х 1=1, xn = xn – 1+2.
Решение. 1) Подставляя последовательно n =1, 2, 3, 4, … в формулу для общего члена последовательности, найдем: х 1= –1; 
; 
; 
;
2) В соответствии с формулой xn=xn – 1+2 получим: х 2= х 1+2=3, х 3= х 2+2=5, х 4= х 3+2=7.
Задание. Какие из следующих последовательностей ограничены сверху? снизу? ограничены?
1) 2; 4; 6; 8; …
2) –1; –4; –9; –16; …
3) –2; 4; –8; 16; ….
Решение. 1) Данная последовательность, состоящая из всех чётных положительных чисел, ограничена снизу, но не ограничена сверху;
2) xn = – n 2<0 (n =1, 2, 3, …), последовательность ограничена сверху, но не ограничена снизу;
3) xn =(–2) n не ограничена, так как для любого числа M >0 можно найти такой номер n, что |xn|=2 n > M.
Задание. Какие из последовательностей монотонные, а какие — строго монотонные: 1) xn =2 n +1; 2) –1; –1; –2; –2; –3; –3; …
Решение. 1) данная последовательность строго возрастает, т.к. xn +1=2(n +1)+1=2 n +3>2 n +1= xn для всех натуральных чисел n;
2) данная последовательность невозрастающая, так как 
, n =1, 2, … и некоторые (например, первый и второй) члены этой последовательности равны между собой.
Задание. Доказать, что 
есть бесконечно малая.
Решение. Запишем последовательность значений:
–1, – 
, – 
, – 
, …, 
, …
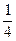отсюда видно, что с возрастанием n значения переменной xn приближаются к нулю так, что с некоторого номера N абсолютные значения переменной будут меньше любого наперёд заданного сколь угодно малого положительного числа 
. Докажем это. Пусть дано >0, тогда 
или 
< , отсюда n > 
, следовательно, можно принять номер N > , при значении которого для любых номеров n 
N будет выполняться неравенство 
. Пусть, например, ε=0,01, тогда 
для всех n N, где 
.
Если ε= 
, то 
, т.е. можно принять номер N =3. Следовательно, значения переменной по абсолютной величине 
для всех номеров 
. Это и означает, что переменная xn есть бесконечно малая величина.
Постановка задачи. Пользуясь определением последовательности, доказать, что 
.
План решения. 1. Число а называется пределом последовательности { xn }, если для 
, 
. Это означает, что неравенство 
имеет решение для 
.
2. Найти, при каких n справедливо неравенство , т.е. решить это неравенство относительно n.
3. Если решение имеет вид , то а — предел числовой последовательности { xn }.
⋙Если решение неравенства нельзя представить в виде , то число а не является пределом последовательности { xn }.
Задание. Пользуясь определением предела последовательности, доказать, что 
.
Решение. 1. По определению число а =2 называется пределом числовой последовательности 
, если 
.
2. Найдём, при каких n справедливо неравенство , т.е. решим это неравенство относительно n.
3. Неравенство имеет решение 
. Следовательно, 2 — предел числовой последовательности .
Задание. Вычислить предел.
Решение. 
1
Задание. Вычислить предел.
Решение. 
= 
0
