Пример 1. Осуществить расчеты влияния факторов (табл.1) с помощью способов элиминирования (цепных подстановок, абсолютных разниц и проч.).
Таблица 1
| Показатели | Условные обозначения | По плану | Факт | Абс. отклонение | % выполнения плана | Отклонения в % |
| Численность работников, чел. | Ч | -2 | 94,286 | 5,714 | ||
| Производительность труда, тыс. грн. | СВ | 116,667 | 16,667 | |||
| Выпуск продукции (за год) | ВП |
Методические рекомендации к решению задачи:
1. Способ цепных подстановок
Создаем факторную модель объема выпуска продукции за год:
ВП = СВ х Ч;
ВПпл = СВпл х Чпл = 1200 х 35 = 42000 (тыс.грн.);
ВПум = СВ ф х Чпл = 1400 х 35 = 49000(тыс.грн.)
ВПф = СВф х ЧФ = 1400 х 33 = 46200(тыс.грн.).
Изменение выпуска продукции за счет производительности труда:
ΔВПсв = ВПум - ВПпл. = 7000(тыс.грн.).
Изменение выпуска продукции за счет численности:
ΔВП ч = ВП ф - ВП ум = - 2800 (тыс.грн.).
Проверка:
46200 – 42000 = 4200 (тыс.грн.), 7000 + (- 2800) = 4200(тыс.грн.).
2. Способ абсолютных разниц:
ΔВП ч = (Чф - Чпл) х СВпл = (33 - 35) х 1200 = - 2400 (тыс. грн.);
ΔВПсв = Чф х (СВф - СВпл) = 33 х (1400 - 1200) = 6600(тыс.грн.).
За счет сокращения численности рабочих на 2 чел. объем продукции уменьшился на 2400 тыс.грн. За счет роста производительности труда на 200 тыс. грн./чел, дополнительно получено 6600 тыс. грн. продукции.
Резерв в выпуске продукции составляет 2400 тыс. грн.
Определяем общее влияние факторов:
Δ ВПсв + ΔВПч = (- 2400) + 6600 = 4200 (тыс. грн).
3. Способ процентных разниц
Определяем влияние фактора численности работников:
(-5,72 х 42000): 100 = 2402,4 (тыс. грн).
Определяем влияние фактора производительности труда:
(15,72 х 4200): 100 = 6602,4(тыс. грн).
Уменьшение количества работников на 5,72% привело к уменьшению объема продукции на 2402,4(тыс. грн).
Пример 2. Цена изделия на рынке - 4,6 грн / ед., прямые затраты на изделие - 2,36 грн., годовая сумма постоянных затрат - 652 тыс.грн. При каком объеме производства предприятие не будет иметь убытков?
Методические рекомендации к решению задачи:
Для безубыточной деятельности предприятие должно работать так, чтобы выручка от реализации (Р) достигла как минимум суммы затрат (С), то есть: Р = С.
Р = д · р,
С = П + Зод,
р д = П + Зо д,
П = р д – З о д,
д= П / (р-Зо).
Таким образом: 65200: (4,6 - 2,36) = 291,1 тыс.грн.
Условные обозначения:
Зо - переменные затраты на единицу продукции,
д – количество изделий,
П- сумма постоянных затрат,
Р - цена единицы продукции.
Пример 3. Определить зависимость выпуска от запуска изделий на поточной линии, используя такую совокупность наблюдений (табл.2):
Таблица 2
Запуск, 
| 78,408 | 95,832 | 56,628 | 87,12 | 65,34 | 60,984 |
Випуск, 
| 73,93 | 89,831 | 49,8583 | 80,375 | 60,604 | 55,446 |
Определить основные характеристики корреляционной зависимости между y и x.
Методические рекомендации к решению задачи:
1.Определим средние величины x и y.
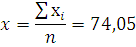
2. Для дальнейших расчетов проведем предварительные вычисления. Их результаты представим в табл.3.
Таблица 3
| 
| ()()
|
| 4,36 | 5,59 | 24,35 |
| 21,78 | 21,49 | 468,06 |
| -17,42 | -18,48 | 322,04 |
| 13,07 | 12,03 | 157,26 |
| -8,71 | -7,74 | 67,40 |
| -13,07 | -12,89 | 168,51 |
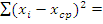 1214,38
|  1205,63
|  1207,62
|
3.Рассчитаем величину коэффициента корреляции для определения тесноты связи между у и х по формуле:
Где
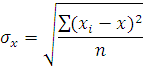
И
Подставляя соответсвующие значения, получаем:
Отсюда
Поскольку коэффициент корреляции довольно высокий (R>0,5), выбираем линейную форму зависимости, которая имеет вид
Для определения параметров уравнения решим систему линейных уравнений:
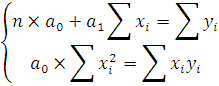
Анализируя систему уравнений, видим, что неизвестными для решения являются 
и 
. Эти величины рассчитываемвуємонняіты связи9,6 (тив в табл.4.
Таблица 4
| 6147,8 | 9183,8 | 3206,7 | 7589,9 | 4269,3 | 3719,1 | =34116,58
|
| 5796,7 | 8608,7 | 2823,4 | 7002,3 | 3959,9 | 3381,3 |  31572,22
|
Тогда получим систему нормальных уравнений:
из системы определим величины 
и 
:
-5,34
=1,15
4. Значит, уравнение регресии имеет вид
5. Проверим
Вывод: анализ свидетельствует о том, что взаимосвязь между исследуемыми величинами (х и у) очень тесный (R=0,99). Полученная линейная формула зависимости дает возможность довольно точно прогнозировать величину запуска в производство изделий для получения необходимого количества качественных товаров.
Пример 4. Используя теорию игр, проанализируйте ситуацию, когда игроками являются природа и предприятие, которое изготавливает жалюзи и стеклопакеты. Оптимизируйте среднюю величину дохода предприятия, несмотря на погоду.
Затраты предприятия на единицу продукции составляют: жалюзи─5 усл.ед., стеклопакеты─18 усл.ед. Цена реализации равна: жалюзи─11 усл.ед., стеклопакеты─32 усл.ед.
Статистические данные за несколько лет свидетельствуют, что предприятие реализует по теплой погоде─681 стеклопакетов и 2349 жалюзи; при холодной погоде─1236 стеклопакетов и 739 жалюзи.
Методические рекомендации к решению задачи:
1.Определим стратегии
-предприятия:
Стратегия А─при теплой погоде;
Стратегия В─при холодной погоде;
-природы:
Стратегия С─при теплой погоде;
Стратегия D─при холодной погоде.
2.Рассчитаем доход предприятия при разных комбинациях стратегий предприятия и природы:
-при стратегии предприятия А и стратегии природы С вся продукция будет реализована и доход будет составлять:
681×(32-18)+2340×(11-5)=23574
-при стратегии предприятия А и стратегии природы D доход предприятия составит:
681×(32-18)+739×(11-5)-(1236-681)×32,4=31950
-при стратегии предприятия В и D природы доход предприятия составит:
1236×(32-18)+739×(11-5)=21738
-при стратегии предприятия В и природы С доход предприятия составит:
2340×(11-5)+1236×(32-18)-(739-2349)×6=41004
2. Рассматривая предприятие (
) и природу (
) как двух игроков, построим матрицу платежей в виде таблицы 5.
Таблица 5
| Игроки | Природа ()
| |||
| Предприятие ()
| Стратегия | C | D | Min по строчке |
| А | ||||
| В | ||||
| Max по столбцу |
Из матрицы видно, что предприятие получит наибольший доход, который составляет 41004 гр.ед., а наименьший 21738 гр.ед.
Очевидно, что следует выбрать смешанную стратегию, которая сложилась из отдельных элементов «чистых стратегий» А и В.
4.Обозначим частоту применения игроком стратегии А через х. Тогда частота применения В (1-х). Если игрок в использует оптимальную смешанную стратегию, то при стратегии природы С(тепло) и D(холод) доход предприятия должен быть одинаковым:
41004 х -21738 
(1- х)=23574 х +31950×(1- х)
х=0,755
1-х=0,245
5.Значит игрок будет иметь в процессе использования стратегий А и В в соотношении 0,755:0.245 доход в сумме:
- при использовании стратегии С:
41004×0,755+21738×0,245=25626,12 усл. ед.
- При использовании стратегии D:
23574×0,755+31950×0,245=25626,12 усл. ед.
Такой одинаковый доход называют средним платежем или ценой игры.
6. Определим, какое количество стеклопакетов и жалюзи предприятие должно изготавливать для обеспечения гарантированного среднего дохода:
(681с+2340ж)×0,755+(1236с+739ж)×0,245=817с+1948ж.
Выводы: изготавливая 817 стеклопакетов и 1948 жалюзи, предприятие стабильно будет рабо тать при любой погоде, получая доход 25629 усл. ед.
Пример 5.
Определить возможность отклонения уровня рентабельности в будущем году, если известно, что она за предыдущие годы составляет:
2000 год – 10%;
2001 год – 11%;
2002 год – 8%;
2003 год – 9%;
2004 год – 11%;
2005 год – 7%;
2006 год – 10%;
2007 год – 9%;
2008 год – 8%;
2009 год – 10%.
Методические рекомендации к решению задачи:
Расчет дисперсии рентабельности предприятия представлен в таблице 6.
Таблица 6.
Расчет дисперсии рентабельности предприятия
| Уровень рентабельности, % | Количество случав наблюдения | Вероятность | Дисперсия |
| 0,1 | (7-9,3)2  0,1=0,529
| ||
| 0,2 | (8-9,3)2 0,2=0,338
| ||
| 0,2 | (9-9,3)2 0,2=0,018
| ||
| 0,3 | (10-9,3)2 0,3=0,147
| ||
| 0,2 | (11-9,3)2 0,2=0,578
| ||
| Итого | 1,0 | 1,61 |
1. Средне ожидаемое значение рентабельности составляет:
(%).
2. Стандартное средне квадратическое отклонение составляет:
3. Коэффициент вариации (В) составляет:
.
Выводы: отклонение уровня рентабельности в будущем году может составлять 13,65% от среднего значения.
