Числовые характеристики выборки вычисляются по следующим формулам:
- эмпирическое (выборочное) среднее
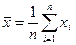; (4)
- выборочная дисперсия
, или 
; (5)
- стандартное отклонение
, или 
; (6)
- размах выборки
; (7)
- эмпирический центральный момент 
-го порядка
, или 
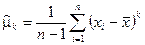; (8)
- эмпирические коэффициенты асимметрии и эксцесса
, 
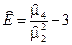. (9)
Несмещенные оценки коэффициентов асимметрии и эксцесса вычисляются по формулам:
, 
, (10)
где
, 
.
Вторая формула (5) дает несмещенную оценку дисперсии 
, но, несмотря на это, после извлечения квадратного корня (формула (6)) получается смещенная (несколько преуменьшенная) оценка для среднеквадратичного отклонения. Несмещенная оценка 
получается после введения поправочного коэффициента 
, зависящего от объема выборки:
, 
, (11)
где 
- гамма-функция Эйлера. Использовать эту формулу имеет смысл лишь при малом объеме выборки, поскольку множитель при больших значениях 
приблизительно равен единице и очень слабо изменяется с ростом : 
; 
; 
; 
.
Отметим, что оценки математического ожидания и дисперсии 
и 
являются несмещенными оценками при произвольных распределениях, оценка стандартного отклонения (11) может быть смещенной при распределениях, отличных от нормального распределения.
Порядок выполнения задания
- Присвойте переменной ORIGIN значение равное единице.
- Из файла с именем «Lab1 Nx», где N – номер варианта задания, считайте исходные данные и разместите их в массиве Х.
- С помощью встроенной функции length (X) определите объем выборки – .
- Определите максимальное и минимальное значения и размах выборки.
- Выполните операцию ранжирования выборки.
- Задайте (или вычислите) число
интервалов группирования данных. - Вычислите характеристики интервалов группированной выборки:
, 
, 
, 
. - Определите с помощью встроенной функции hist(x,X) массив значений (вектор) относительных частот.
- Постройте гистограмму и полигон относительных частот, используя различные стили графического оформления результатов.
- Сравните гистограмму (полигон) с теоретической плотностью вероятностей.
- Определите оптимальное значение количества интервалов группированной выборки ; все дальнейшие вычисления проводите при этом значении .
- Определите массив (вектор) относительных накопленных частот.
- Постройте графики эмпирической функции распределения по исходной и группированной выборке, сравните результаты.
- Сравните эмпирическое и теоретическое распределения (изобразив на одном графике эмпирические полигоны частот и указанное в задании распределение).
- Вычислите все указанные в задании числовые характеристики выборки с использованием формул (4) – (11) и встроенных функций системы Mathcad. Сравните результаты вычислений.
- Используя квантиль
распределения Колмогорова, постройте доверительную область для эмпирической функции распределения. Обратите внимание на то, как изменяется «ширина» доверительной области с изменением 
. - Сформулируйте выводы по проделанной работе.
- Сохраните рабочий документ.
При определении оптимального значения количества интервалов группированной выборки (пункт 11.) можно воспользоваться приведенной ниже Маткад-программой Gist(X,m) (или аналогичной программой, составленной самостоятельно). Параметры этой программы: X – массив, содержащий числовые значения элементов выборки, m – количество интервалов группировки данных.
Обратившись к этой программе с различными значениями параметра и построив соответствующие графики, оптимальное значение можно определить визуально, «на глаз». Проделав эту работу, сравните полученное вами оптимальное значение с приведенными выше рекомендациями.
