Лекция 5. ПРЕДЕЛЫ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Числовую функцию f(n) = an, заданную на множестве натуральных чисел (n ÎN), называют числовой последовательностью. Говорят, что последовательность задана, если каждому натуральному числу n по некоторому закону f поставлено в соответствие число f(n). В том случае, когда закон f задан формулой, говорят об аналитическом задании последовательности, при этом, как правило, записывают аналитическое выражение для члена аn, называемого общим членом последовательности. Например, последовательность квадратов целых чисел: 1, 4, 9, 16, 25,.., n2,... = { n 2}.
Часто закон, по которому задается последовательность, позволяет построить очередной член последовательности по известным предыдущим. Такой способ задания называется рекуррентным. Хорошо известная арифметическая прогрессия а, а + d, а + 2d, а + 3d,...= { а + (n-1)d }может быть задана при помощи рекуррентного соотношения: аn = аn-1 + d.
Геометрическая прогрессия b, bq, bq2, bq3,...= { bqn-1 } может быть задана при помощи следующего рекуррентного соотношения: bn+1 = bn q.
Для полного задания последовательности, кроме рекуррентного соотношения, необходимо задать некоторое число первых членов последовательности. Так, для арифметической и геометрической последовательностей, из бесконечного числа членов достаточно задать лишь их первые члены а и b, а также и параметры прогрессий d и q.
Последовательность { xn } называется ограниченной сверху, если существует число М (верхняя граница), такое, что, xn < M для всех n.
Последовательность { xn } называется ограниченной снизу, если существует такое число m (нижняя граница), что xn > m для всех n.
Если для всех членов последовательности выполняется условие xn > xn-1, то она называется возрастающей.
Если для всех членов последовательности выполняется условие xn < xn-1, то она называется убывающей.
Поскольку для всех n кроме того выполняется условие, то это последовательность.
Последовательность { xn } называется ограниченной, если она ограничена и сверху и снизу.
Вторая из приведенных выше последовательностей является ограниченной снизу возрастающей последовательностью.
Пример.Рассмотрим далее три последовательности:
1, 0, -1, -2, -3,......, - п,....;
2, 4, 6,......2 n, …...;
1, 2-1, 2-2, 2-3, ……., 2-n ….
Первая из приведенных выше последовательностей ограничена сверху, например, числом 2 и является убывающей.
Вторая из приведенных выше последовательностей ограничена снизу, например, числом 1 и является возрастающей.
Третья последовательность является ограниченной убывающей последовательностью.
Последовательность { хn } называется бесконечно большой, если для любого положительного числа А (сколь бы большим его ни взяли) существует номер N такой, что для всех членов последовательности с номерами n > N выполняется неравенство | хn | > А.
Последовательность { xn } называется бесконечно малой, если для любого положительного числа ε>0 (сколь бы малым его ни взяли) существует номер N такой, что для всех членов последовательности с номерами n > N выполняется неравенство | xn | < ε.
Рассмотрим последовательность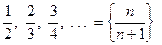 
Члены этой последовательности по мере возрастания номера члена приближаются к числу 1. Говорят, что эта последовательность сходится к числу 1.
Строгое определение может быть дано следующим образом.
Последовательность {xn} сходится к числу А, если для любого сколь угодно малого числа ε > 0 можно указать такое натуральное число N(ε), что для всех n больше N, то есть для n > N выполняется неравенство |xn ‒ А| < ε.
То что А является пределом { xn } записывается так: 
. Говорят также, что xn стремится к А и пишут 
.
Проиллюстрируем это определение на приведенном выше примере сходящейся последовательности:
.
Пусть ε = 0,01, тогда неравенство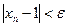 
преобразуется 
и далее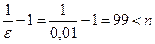 
. Значит неравенство 
выполняется при всех 
, значит найдено искомое 
.
Найдем N(0,0001). 
отсюда 
.
Тем самым установлено, что, начиная с n = 99, будет выполняться неравенство | xn — 1| < 0,01, а начиная с n = 9999, будет выполняться неравенство | xn — 1| < 0,0001.
Теперь можно записать, что 
.
Каждому члену числовой последовательности (поскольку это число) соответствует точка на числовой оси. Если последовательность имеет пределом число с соответствующей точкой А, то для всех номеров последовательности, начиная с некоторого N, точки соответствующие членам последовательности находятся внутри промежутка (А - ε, А + ε), называемого ε-окрестностью числа А.
Если ε очень мало, то число N может быть весьма большим. Следовательно, большое количество членов последовательности окажутся вне ε-окрестности, однако их всегда будет лишь конечное число. Все остальные члены последовательности, начиная с номера N и более, попадают в ε-окрестность. Таким образом, если последовательность сходится к А, то какую бы окрестность точки А ни взять, почти все числа xn попадают в выбранную окрестность.
Отсюда следует, что добавление или исключение конечного числа членов такой последовательности не влияет на ее сходимость. Если последовательность { xn } сходится к А, то пишут: 
(читается: «предел xn при n, стремящемся к бесконечности, равен А»). В этом случае говорят, что число А есть предел последовательности { xn } или иначе, при неограниченном увеличении номера общий член последовательности стремится к величине А.
Последовательность {xn} называется бесконечно большой, если для любого сколь угодно большого числа E можно указать такое натуральное число N(E), что для всех n больше N(E), то есть для n > N(E) выполняется неравенство |xn| > E.
Если при этом начиная с некоторого номера xn> 0, то говорят, что xn имеет предел 
или 
. Если же начиная с некоторого номера xn < 0, то говорят, что xn имеет предел 
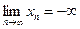или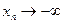 
.
Если последовательность не имеет конечного предела или не имеет предела вообще, то ее называют расходящейся. Так, последовательность -1, 1, -1, 1,... (-1)n,... расходится, так как в этом случае 
не существует. А последовательность -1, 0, -1, -2, -3,......, - п,.... расходится, так как не имеет конечного предела, хотя .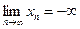
