При изучении движения жидкости интенсивность массовых сил  обычно считается известной. Неизвестными являются функции
обычно считается известной. Неизвестными являются функции  ,
,  ,
,  ,
,  – всего четыре неизвестных функции. Определяемые функции должны удовлетворять уравнениям Эйлера (6.5). Поскольку число неизвестных превышает число уравнений, к уравнениям Эйлера необходимо присоединить уравнение неразрывности в дифференциальной форме.
– всего четыре неизвестных функции. Определяемые функции должны удовлетворять уравнениям Эйлера (6.5). Поскольку число неизвестных превышает число уравнений, к уравнениям Эйлера необходимо присоединить уравнение неразрывности в дифференциальной форме.
Уравнение неразрывности, записанное для элементарного объема жидкости в форме прямоугольного параллелепипеда размерами  (см. рис.6.1) можно получить на основании следующих рассуждений.
(см. рис.6.1) можно получить на основании следующих рассуждений.
Гипотеза сплошности, применительно к идеальной жидкости, предполагает, что за время 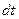 объемы жидкости втекающей и вытекающей из элементарного параллелепипеда должны быть равны. Объемы жидкости втекающей через грани перпендикулярные осям
объемы жидкости втекающей и вытекающей из элементарного параллелепипеда должны быть равны. Объемы жидкости втекающей через грани перпендикулярные осям  легко найти по составляющим скорости
легко найти по составляющим скорости 
 . .
| (6.28) |
Аналогичные объемы вытекающей жидкости, с учетом изменения скорости, равны
 . .
| (6.29) |
Сплошность в рассматриваемом объеме не нарушится, если
  , ,
| (6.30) |
что после подстановки (6.28) и (6.29) в (6.30) приводит к результату

| (6.31) |
Уравнение (6.30) и есть уравнение неразрывности идеальной несжимаемой жидкости в дифференциальной форме.
Присоединив к уравнениям равновесия (6.5) уравнение неразрывности (6.31) получаем систему дифференциальных уравнений для определения четырех функций, характеризующих установившееся движение жидкости.



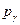
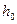


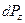





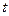



 –
– 
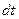


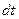



 О
О
Уравнение Бернулли для струйки в поле силы тяжести
Если ось  направить по линии действия силы тяжести вверх, то из (6.12) получим
направить по линии действия силы тяжести вверх, то из (6.12) получим
 , ,  , ,  , , 
| (6.32) |
и уравнение (6.15) принимает вид

| (6,33) |
или
  
| (6.34) |
Если записать уравнение Бернулли для частицы жидкости при установившемся движении в двух ее положениях на линии тока (она совпадает с траекторией), то получим
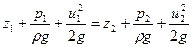
| (6.35) |
Уравнение Бернулли для струйки в криволинейном канале,
вращающемся с постоянной угловой скоростью
В том случая, когда жидкость движется в криволинейном канале, вращающемся с постоянной угловой скоростью, и линия действия силы тяжести параллельна оси вращения канала (рис.6.4), массовые силы, включая силу инерции в переносном движении, отнесенные к единице массы равны
 . .
| (6.36) |
Здесь учтены силы инерции в переносном движении, связанные с нормальным ускорением и сила тяжести. Сила инерции, определяемая кориолисовым ускорением, не рассматривается, т.к. она не влияет на движение частицы жидкости в направлении ее относительного движения.
Тогда, полагая
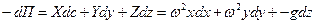 , ,
| (6.37) |
после интегрирования найдем потенциал массовых сил
 , ,
| (6.38) |
или
 . .
| (6.39) |
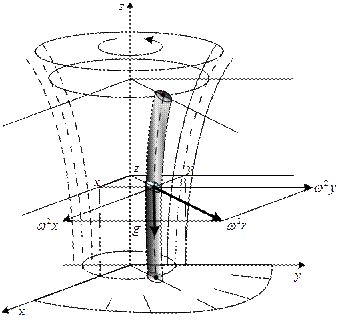 Рис.6.4
Рис.6.4
|
Уравнение Бернулли (6.15) принимает вид
 , ,
| (6.40) |
или
 . .
| (6.41) |
Для двух сечений элементарной струйки можно записать
 . .
| (6.42) |
Здесь  есть угловая скорость в переносном движении.
есть угловая скорость в переносном движении.
Геометрическая интерпретация уравнения Бернулли для струйки идеальной жидкости
Каждое слагаемое в уравнении (6.34) можно рассматривать, как составляющую энергии частицы, отнесенную к единице веса.
Если за плоскость сравнения принять плоскость с нулевой потенциальной энергией, то:
- потенциальная энергия единицы веса определится формулой
 ; ;
| (6.42) |
- удельная кинетическая энергия составит
 ; ;
| (6.42) |
- удельная энергия давления будет равна
 . .
| (6.42) |
Для удельной энергии и ее составляющих, в гидравлике применяют следующие термины и обозначения:
H - гидродинамический или полный напор;
z - геометрический напор;
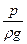 - пьезометрический напор;
- пьезометрический напор;
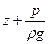 - гидростатический напор;
- гидростатический напор;
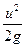 - скоростной или кинетический напор.
- скоростной или кинетический напор.
|
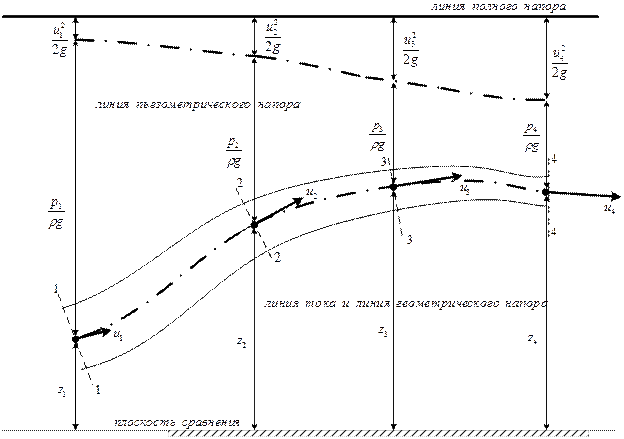
Рис. 6.5. Геометрическая интерпретация уравнения Бернулли для струйки идеальной жидкости.
Единицей измерения напора является единица длины. Ясно, что при движении идеальной жидкости отдельные составляющие полного напора могут изменяться, но полный напор остается величиной постоянной (рис. 6.5).
Лекция 7
Уравнение Бернулли для струйки реальной жидкости
потока реальной жидкости. Режимы движения жидкости
Уравнение Бернулли для струйки вязкой жидкости
Течение реальной жидкости, в отличие от течения идеальной, характеризуется наличием потерь энергии на преодоление сил сопротивления движению – в первую очередь это потери на преодоление сил трения, обусловленных вязкостью жидкости и ее трением о стенки канала. Поэтому в правую часть формулы (6.35) необходимо добавить слагаемое, которое и будет учитывать потери энергии струйки
 , ,
| (7.1) |
где 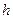 -- потери напора на участке между сечениями 1-1 и 2-2.
-- потери напора на участке между сечениями 1-1 и 2-2.
Энергия, затраченная на преодоление сил вязкого трения, превращается из механической энергии в энергию тепловую. Процесс носит необратимый характер.
Уравнение Бернулли для потока вязкой жидкости
при установившемся движении
Если движение жидкости установившееся и плавно изменяющееся происходит в направлении оси x, то
  ; ;  ; ;  . .
| (7.2) |
В этом случае давление по живому сечению потока распределяется по гидростатическому закону, т.е.
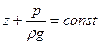 . .
| (7.3) |
Если поле скоростей имеет искривленные линии тока, гидростатический закон распределения давления в живом сечении нарушается, но при достаточной плавности потока этим фактом можно пренебречь (рис.7.1).
 Рис. 7.1
Рис. 7.1
|
При переменной по сечению скорости частиц жидкости ( ), удельную кинетическую энергию массы жидкости, протекающей через живое сечение потока A можно рассчитать по формуле
), удельную кинетическую энергию массы жидкости, протекающей через живое сечение потока A можно рассчитать по формуле
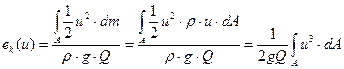 , ,
| (7.4) |
где 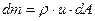 - масса жидкости, которая прошла через сечение за единицу времени.
- масса жидкости, которая прошла через сечение за единицу времени.
В общем случае вычисления по формуле (7.4) невозможны, т.к. функция  неизвестна. Целесообразно воспользоваться средней скоростью потока в сечении v
неизвестна. Целесообразно воспользоваться средней скоростью потока в сечении v
 . .
| (7.5) |
Заменить в уравнении Бернулли для потока удельную кинетическую энергию  на
на 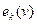 можно, если ввести коэффициент кинетической энергии (коэффициент Кориолиса)
можно, если ввести коэффициент кинетической энергии (коэффициент Кориолиса)
 . .
| (7.6) |
В этом случае
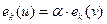 . .
| (7.7) |
Коэффициент  определяется для всех практически значимых случаев течения потока экспериментально и характеризует отношение действительной кинетической энергии массы жидкости, протекающей через живое сечение потока, к кинетической энергии той же массы жидкости, вычисленной по средней скорости потока в сечении.
определяется для всех практически значимых случаев течения потока экспериментально и характеризует отношение действительной кинетической энергии массы жидкости, протекающей через живое сечение потока, к кинетической энергии той же массы жидкости, вычисленной по средней скорости потока в сечении.

| Условия движения жидкости | ||
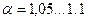
| - при прямолинейном турбулентном течении в трубах; | ||

| - при прямолинейном турбулентном течении в открытых каналах; | ||

| - при прямолинейном ламинарном течении в трубах (теоретическое решение). |
Вводя в рассмотрение средние значения геометрического напора z и пьезометрического напора 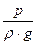 , запишем для плавно изменяющегося потока, ограниченного жесткими стенками (канал, русло, трубопровод) уравнение Бернулли
, запишем для плавно изменяющегося потока, ограниченного жесткими стенками (канал, русло, трубопровод) уравнение Бернулли
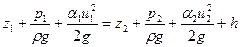 . .
| (7.8) |
Графическое толкование уравнения Бернулли для потока вязкой жидкости в предположении, что потери напора h линейно зависят от длины канала, приведено на рис. 7.2, где  - потери напора на участке между сечениями 1-2, 1-3, 1-4 соответственно. Линия полного напора в этом случае не остается горизонтальной, как при движении идеальной жидкости, а представляет линию нисходящую по направлению движения потока.
- потери напора на участке между сечениями 1-2, 1-3, 1-4 соответственно. Линия полного напора в этом случае не остается горизонтальной, как при движении идеальной жидкости, а представляет линию нисходящую по направлению движения потока.
Для характеристики потерь напора на регулярном участке потока используют понятие гидравлического уклона. Гидравлический уклон – это величина средних потерь напора на единицу длины канала
 . .
| (7.9) |
Локальное гидравлического уклона характеризует скорость уменьшения полного напора потока по направлению его движения
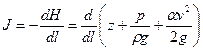 . .
| (7.10) |
 Рис.7.2.
Рис.7.2.
|
Классификация потерь напора
Потери напора при движении вязкой жидкости подразделяют на:
· потери напора на преодоление гидравлического сопротивления по длине, которые пропорциональны длине участков русла или трубы, направляющей движение потока;
· потери на преодоление гидравлических сопротивлений в пределах коротких участков, на которых имеются различные конструктивные нерегулярности – резкое сужение или расширение русла, внезапное увеличение или уменьшение диаметра трубы, поворот трубы или русла, устройства входа или выхода, трубопроводная арматура (краны, задвижки, разветвления и т.д.).

| (7.11) |
Обычно потери напора определяют через скоростной напор и соответствующий коэффициент сопротивления 
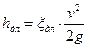 , ,
| (7.12) |
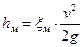 . .
| (7.13) |
Большинство зависимостей для определения коэффициентов сопротивления  или их конкретные значения установлены экспериментальным путем. На значения коэффициентов сопротивления влияет множество факторов:
или их конкретные значения установлены экспериментальным путем. На значения коэффициентов сопротивления влияет множество факторов:
· конструктивные формы и размеры;
· шероховатость стенок канала или трубы;
· скоростной режим течения жидкости;
· положение управляющих элементов запорной арматуры.
Одна из общих формул для определения потерь по длине – формула Дарси-Вейсбаха, для круглых труб имеет вид
 , ,
| (7.14) |
где  - коэффициент гидравлического трения;
- коэффициент гидравлического трения;
l - длина трубопровода;
d – диаметр трубы.
Очевидно, что в этом случае  .
.
Коэффициенты местного сопротивления определяются исключительно экспериментальным путем и их значения можно найти в справочниках и учебниках. Обычно в формуле (7.12) коэффициент 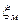 определяется применительно к скоростному напору за местным сопротивлением (рис.7.3)
определяется применительно к скоростному напору за местным сопротивлением (рис.7.3)
 Рис. 7.3
Рис. 7.3
| 
|
Режимы движения жидкости
Экспериментально установлено существование двух основных видов движения жидкости – ламинарного и турбулентного.
Ламинарным называют такой режим течения жидкости, когда все линии тока направлены параллельно оси канала, когда слои жидкости двигаются без перемешивания частиц и пульсаций скорости.
При турбулентном движении слои жидкости интенсивно перемешиваются, движение частиц не носит упорядоченного характера, траектории имеют вид замысловатых линий, наряду с основным перемещением в направлении оси канала малые объемы жидкости вращаются и перемещаются в направлении перпендикулярном оси канала.
Наглядно особенности течения при разных режимах можно наблюдать с помощью экспериментальной установки, в которой жидкость перемещается в стеклянной трубе, а для визуализации течения в основной поток жидкости вводят струйки подкрашенной жидкости с близким значением кинематического коэффициента вязкости. Схема установки и примерная картина изменения формы струйки подкрашенной жидкости показаны на рис. 7.4.
В расходном баке 1 с помощью внутренней перегородки 9 поддерживается постоянный уровень жидкости, что обеспечивает, при установленном с помощью крана 6 расходе жидкости, постоянную скорость ее движения в стеклянной трубке 2. К установившемуся потоку жидкости в трубке 2 подмешивается струйка подкрашенной жидкости из расходного бачка 3, которая подается через кран 4 по трубке 5.
До определенной скорости движения жидкости по трубке 2 заметного обмена частицами жидкости между окрашенной струйкой и окружающей ее жидкостью не происходит. Если в поток вводить несколько струек подкрашенной жидкости, то все они перемещаются не смешиваясь с остальной массой жидкости. Это позволяет утверждать, что при установленной скорости движения жидкость движется отдельными слоями не перемешивающимися между собой. Линии тока при этом прямолинейны и устойчивы. Средняя скорость движения жидкости, до которой наблюдается описанное явление, называют критической -  .
.
При увеличении скорости течения до значения больше критического, окрашенные струйки начинают искривляться; а при еще большем увеличении - струйки распадаются на отдельные хорошо различимые вихри, интенсивно перемешивающиеся с остальной массой жидкости.
При уменьшении скорости потока после достижения турбулентного режима течения явление повторяется в обратном порядке, но с одним отличием – скорость, на которой происходит переход от турбулентного режима течения к ламинарному оказывается меньше, чем при переходе от ламинарного к турбулентному. Ламинарный и турбулентный режимы отличаются величиной сопротивления движению потока. Потери напора при турбулентном движении больше. Качественно зависимость гидравлического уклона от скорости потока представлена на рис. 7.5.

 Рис. 7.4.
Рис. 7.4.
|
В диапазоне скоростей 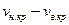 движение жидкости считают смешанным; при
движение жидкости считают смешанным; при  – ламинарным, а при
– ламинарным, а при  – турбулентным. Абсолютное значение критических скоростей зависит от кинематической вязкости жидкости и геометрических параметров живого сечения.
– турбулентным. Абсолютное значение критических скоростей зависит от кинематической вязкости жидкости и геометрических параметров живого сечения.
 Рис. 7.5
Рис. 7.5
|
Для труб круглого сечения при напорном движении потока нижняя критическая скорость пропорциональна кинематической вязкости и обратно пропорциональна диаметру трубы
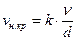 , ,
| (7.15) |
где коэффициент пропорциональности k остается неизменным при различных значениях 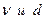 . Теория подобия гидравлических потоков позволила определить этот безразмерный коэффициент, как критическое значение числа подобия – числа Рейнольдса. Значение критического числа Рейнольдса установлено многочисленными экспериментами и равно 2300 для круглых труб.
. Теория подобия гидравлических потоков позволила определить этот безразмерный коэффициент, как критическое значение числа подобия – числа Рейнольдса. Значение критического числа Рейнольдса установлено многочисленными экспериментами и равно 2300 для круглых труб.
 . .
| (7.16) |
Для каналов иной формы поперечного сечения и открытых русел характерный линейный размер необходимо заменить гидравлическим радиусом R, что изменит численное значение критического числа Рейнольдса. Так как для круглой трубы  , формула (7.16) принимает вид (7.17) и может использоваться для вычисления нижней критической скорости
, формула (7.16) принимает вид (7.17) и может использоваться для вычисления нижней критической скорости
 . .
| (7.17) |
Для открытого русла прямоугольного сечения в качестве характерного линейного размера часто выбирают глубину потока h. Если 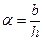 , где b – ширина русла, то легко получить формулу для расчета критического значения числа Рейнольдса
, где b – ширина русла, то легко получить формулу для расчета критического значения числа Рейнольдса  в зависимости от коэффициента
в зависимости от коэффициента 
 . .
| (7.18) |
При  , а при
, а при  .
.






