Построение фазовых траекторий произведем методом изоклин. Определяем изоклины горизонтальных и вертикальных касательных. Приравняем правые части системы (1) к нулю и получим:
с1x1 + a12x1x2=0
с2х2 + a21x1x2=0
Изоклина вертикальных касательных х2=c1/a12 = L1(x1 x2)
Изоклина горизонтальных касательных х2=0=L2(x1 x2)
Изоклины вертикальных и горизонтальных касательных пересекаются между собой и с осями координат в особых точках. Начала фазовых траекторий - это начальные численности популяций. Фазовые кривые стремятся к точкам равновесия (устойчивым узлам).
Г) модели линейной теории автоматического управления
Статикой называется установившийся режим звена или системы, при котором входной и выходной сигналы звена (или системы) постоянны во времени.
Поведение звена (системы) в статике наглядно отражается его статическойхарактеристики, под которой понимается зависимость между установившимися значениями выходной и входной величин.
y вых. уст. = f (x вх. уст.)
По виду статической характеристики различают линейные и нелинейные звенья. Статическая характеристика линейного звена представляет собой уравнение прямой линии:
y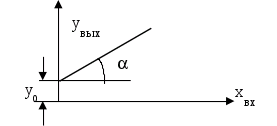 
вых = kxвх+ yo,
где k = tg α
Звенья, статические характеристики которых не являются прямыми линиями, называются нелинейными.
В основном все звенья в природе являются нелинейными.
Вопрос линейности статических характеристик имеет чрезвычайно важное значение. Дело в том, что в динамике САР описываются дифференциальными уравнениями. И если в САР входит нелинейное звено, дифференциальное уравнение получается нелинейным. Решение нелинейных дифференциальных уравнений – процесс трудоёмкий и сложный. Поэтому на практике нелинейные элементы заменяют их линейными моделями для облегчения их описания. Этот процесс называется линеаризацией. Итак, линеаризация нелинейного звена – замена его линейной моделью с сохранением основных свойств нелинейного звена. Простейшими методами линеаризации являются метод касательной, метод секущей и кусочно–линейная линеаризация.
При линеаризации касательной полагают, что в процессе работы объекта рабочая точка статической характеристики будет совершать лишь незначительные колебания вокруг номинального режима и, следовательно, характеристику можно заменить касательной к характеристике в точке А (системы стабилизации).
Для получения уравнения касательной перенесем начало координат в точку А и запишем уравнение касательной в отклонениях от точки номинального режима:
Dу = kDх
В 
еличина 
- отношение выходной величины к входной – статический коэффициент передачи. Для нелинейных звеньев “ к ” – величина не постоянная и зависит от положения рабочей точки А.
М 
етод секущей, может быть, применим к объектам, имеющим нелинейную статическую характеристику, кососимметричную относительно начала координат.
Характеристику такого типа можно заменить линейной секущей АА, причём провести её нужно так, чтобы ошибки ∆ 1, ∆ 2, ∆
