Спутниковая система навигации (GPS - Global Positioning System) - позволяет в любом месте Земли, при любой погоде, а также в космическом пространстве вблизи планеты определить местоположение и скорость объектов.
Для определения координат и высоты приёмника, используются сигналы как минимум с трёх спутников (Рис 1.12).
Рис. 1.12 Спутник системы GPS на орбите.
Основной принцип использования системы — определение местоположения путём измерения расстояний до объекта от точек с известными координатами — спутников.
Расстояние вычисляется по времени задержки распространения сигнала от посылки его спутником до приёма антенной GPS-приёмника.
GPS-приёмники (Рис. 1.13) используются для определения местонахождения и скорости.
Рис. 1.13
GPS-приёмники могут быть выполнены в виде отдельных устройств и встроены в другое оборудование (мобильный телефон)
Функции GPS-приёмников:
— позволяют видеть своё местонахождение на электронной карте;
— имеют возможность прокладывать маршруты с учётом дорожных знаков, разрешённых поворотов и пробок;
— искать на карте конкретные дома и улицы, достопримечательности, кафе, больницы, автозаправки и прочие объекты инфраструктуры.
Однако с использованием GPS-приёмника практически невозможно определить своё точное местонахождение внутри железобетонного здания, в подвале, в тоннеле.
Лазерные дальномеры -ручные лазерные безотражательные дальномеры. Предназначены для измерения расстояний до 200 метров, с точностью до 1,0 мм. Наиболее распространенное название этих приборов - лазерные рулетки.
Электронный тахеометр — геодезический прибор для измерения расстояний, горизонтальных и вертикальных углов. Используется для вычисления координат и высот точек местности при топографической съёмке местности, при разбивочных работах, переносе на местность высот и координат проектных точек.
Достоинства Электронного тахеометра:
— Высокая дальность измерения (500 метров)
— Высокая точность измерения расстояний (±2 мм)
— Высокая скорость измерений расстояний (менее 1 сек)
— Большой объем памяти для хранения данных (>1 Мб) + слот для CF карт памяти.
— Видимый лазерный луч малого диаметра. Позволяет легко выполнять измерения сквозь препятствия.
— Простой экспорт в AutoCAD и другие CAD системы. Загрузка координат в тахеометр.
— Внутреннее программное обеспечение решает не только различные вычислительные задачи, но и предоставляет эффективные средства контроля и анализа измерений.
— определение координат
— высота недоступного объекта
— вычисление площади
— архитектурные обмеры
— проецирование точки
В настоящее время на рынке существует огромное количество разнообразного аппаратного обеспечения, причем организация, внедряющая у себя ГИС, несомненно уже обладает некоторым набором вычислительной техники, поэтому перед ней встает задача использования имеющейся техники с ГИС, из чего вытекает необходимость наличия в системе драйверов — программ, осуществляющих связь с определенным периферийным устройством, и передающих данные от компьютера к устройству и обратно.
ОРГАНИЗАЦИЯ ДАННЫХ В ГИС
2.1 ОРГАНИЗАЦИЯ ПРОСТРАНСТВЕННЫХ ДАННЫХ
ГИС как системы обработки пространственно-временной информа-
ции относятся к классу информационных систем. Они имеют общие,
присущие всему классу, и индивидуальные, присущие только ГИС, свой-
ства. К особенностям ГИС следует отнести наличие больших объемов
хранимой в них информации.
Рис. 2.1
Кроме того, они отличаются специфичностью организации и структурирования моделей данных (Рис. 2.1).
ГИС характеризуются разнообразием графических данных со спе-
цифическими их частями и связями. В частности, карта может быть рас-
смотрена как двухмерная аналоговая модель, отображающая трехмер-
ную поверхность (Рис.2.2).
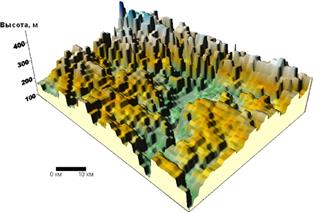Рис. 2.2
Используя процедуры абстракции, определим более общую модель
геоинформационных данных как абстракцию данных, которые содержатся на земной поверхности. Такой подход требует выделения основных типов данных и их многочисленных связей.
Одной из основных моделей в первых ГИС был набор имен и характеристик в сочетании с множеством именованных данных, местонахождение которых задается координатами. Эта простая модель не содержала каких-либо семантических данных, помогающих пользователю при работе с базами данных. Дальнейшие исследования привели к необходимости развития и усложнения такой модели. Другими словами, возникла потребность создания общей модели данных ГИС и ее основных частей для оптимальной обработки в базах данных и эффективного описания объектов.
Данные реального мира, отображаемые в ГИС, можно рассматривать с учетом трех аспектов: пространственного, временного и тематического.
Пространственный аспект связан с определением местоположения, временной - с изменениями объекта или процесса с течением времени, в частности от одного временного среза до другого. Примером временных данных служат результаты переписи населения. Тематический аспект обусловлен выделением одних признаков объекта и исключением из рассмотрения других.
Все измеримые параметры моделей геоинформационных данных подпадают под одну из этих характеристик: место, время, предмет. Затруднительно исчерпывающим образом описать сразу все три эти характеристики. Поэтому при построении моделей данных на основе наблюдений явлений реального мира один параметр считают "неизменным", изменения другого "задаются" и при этом "измеряют" изменения
третьего параметра.
Зафиксировав географическое положение и изменяя время, можно
получить временные ряды данных. Зафиксировав время и изменяя географическое положение, получаем данные по профилям.
В большинстве технологий ГИС для определения места используют один класс данных - координаты, для определения параметров времени и тематической направленности - другой класс данных - атрибуты.
Однако прежде чем рассмотреть два основных класса данных в ГИС, необходимо рассмотреть методы определения местоположения точек объектов на поверхности Земли.
Определение положения точек на поверхности Земли
Координатные данные, составляющие один из основных классов геоинформационных данных, используют для указания местоположения на
земной поверхности.
Поверхность Земли имеет сложную форму. При общей площади ее
поверхности 510 млн. км2 71 % приходится на дно морей и океанов и
29 % - на сушу. Это дает основание считать, что земная поверхность
состоит из двух резко отличающихся морфологических элементов - ма-
териков и океанов.
С учетом того, что поверхность вод Мирового океана занимает по-
чти 3/4 поверхности Земли, за общую фигуру земли принимают тело,
ограниченное поверхностью воды океанов. Такая поверхность называ-
ется уровненной. Потенциал силы тяжести на ней имеет одно и то же
значение. Другими словами, эта поверхность везде перпендикулярна от-
весной линии, т.е. везде горизонтальна.
Можно построить семейство горизонтальных поверхностей. Повер-
хность, которая совпадает с поверхностью Мирового океана в состоя-
нии покоя и равновесия и продолжена под материками, образует фигу-
ру, принятую в геодезии за общую фигуру Земли, называемую геоид.
С помощью методов дистанционного зондирования удалось уста-
новить, что Земля имеет грушевидную форму. В качестве математичес-
кой модели Земли применяют эллипсоид, который в геодезии принято
называть референц-зллипсоидом. В СССР до 1946 г. использовался эл-
липсоид, полученный Ф. Бесселем. В 1946 г: для обязательного исполь-
зования был введен эллипсоид, вычисленный в ЦНИИГАиК в 1940 г.
под руководством Ф.Н. Красовского при участии А.А. Изотова.
Для отображения положения точек поверхности на плоскости ис-
пользуют различные математические модели поверхности и различные
системы координат. На практике применяют два основных типа коорди-
нат: плоские и сферические. Реже применяют криволинейные или по-
лярные.
Выбор системы координат зависит от размеров исследуемых участ-
ков поверхности, как следствие, от влияния кривизны Земли. При изоб-
ражении небольших участков Земли часть уровненной поверхности мож-
но принять за плоскость. Такими участками будут участки до 20 км дли-
ной и площадью до 400 км2.
В этих случаях применимы плоские координаты. Плоские декар-
товы координаты определяются заданием двух осей. При этом обыч-
но координата Х указывает на восток, Y - на север. Задают масштабные
отрезки. Упорядоченная пара (X, Y) определит положение точки в за-
данной системе.
Плоские полярные координаты используют расстояние от начала координат (r) и угол ((r) от фиксированного направления. Направление обычно фиксируется на север, а угол отсчитывается по часовой стрелке от него. Полярные координаты удобны при проведении измерений от какой-либо заданной точки, например, когда используются данные таких источников, как радарные съемки.
При необходимости учета кривизны Земли применяют пространственные системы координат.
Для определения географической системы координат (разновидности сферической системы) введем следующие понятия:
• плоскость земного экватора - проходит через центр Земли перпендикулярно к оси вращения;
• плоскость географического (астрономического) меридиана- проходит через ось вращения Земли и отвесную линию в точке земной поверхности;
• меридиан - линия пересечения плоскостей географических меридианов с земной поверхностью;
• параллель - линия, образованная пересечением плоскости, параллельной плоскости земного экватора, с поверхностью Земли.
Положение точки определяется широтой ((р) и долготой (А.).
Широта - это угол между точкой и экватором вдоль меридиана '.
Она изменяется от -90 ° (южный полюс) до +90 ° (северный полюс).
Долгота - это угол в плоскости экватора между меридианом точки
и главным (нулевым) меридианом, проходящим через Гринвич (Англия).
Она изменяется от -180° (западная долгота) до +180° (восточная дол-
гота).
На рисунке 2.3 изображено измерение широты и долготы для точки на поверхности Земли с координатами 550 с. ш. и 600 в. д.
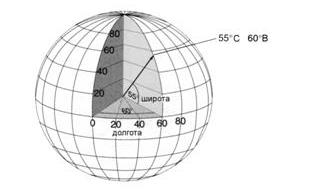Рис. 2.3
Основными понятиями этой системы координат являются:
меридиан - линия постоянной долготы;
параллель - линия постоянной широты;
большой круг - воображаемый круг на земной поверхности, обра-
зованный плоскостью, проходящей через центр земного шара;
малый круг - воображаемый круг на земной поверхности, образо-
ванный плоскостью, не проходящей через центр земного шара.
Рассмотренные системы координат носят в большей степени теоре-
тический характер. На практике используют более широкий набор сис-
тем координат: геоцентрические, топоцентрические, полярные гео-
дезические, эллиптические и др.
Координатные данные
Геометрически информация, содержащаяся на карте, может быть
определена как совокупность наборов точек, линий, контуров и площа-
дей, имеющих метрические значения, отражающие трехмерную реаль-
ность. Эта информация образует класс координатных данных ГИС, являющийся обязательной характеристикой геообъектов. Будучи частью (классом) общей модели данных в ГИС, координатные данные определяют класс координатных моделей.
Основные типы координатных моделей
Класс координатных моделей можно разбить на типы. При этом сле-
дует учесть, что попытка включить в описание широкий набор групп
приводит к усложнению базы данных и процессов обработки. В ГИС
используют меньшее число атомарных моделей по сравнению с САПР.
В ГИС, как и в САПР, применяют набор базовых геометрических
типов моделей, из которых создают все остальные, более сложные. С
учетом предметной области карт ограничиваются лишь описанием та-
ких типов (структур географических данных), которые относятся к пред-
ставлению топографии и к тематическому упорядочению.
В ГИС включают следующие основные типы координатных данных:
• точка (узлы, вершины) (см. Рис. 2.4);
Рис. 2.4 Отображение точечных объектов.
;
• линия незамкнутая (см. Рис. 2.5);
Рис. 2.5 Отображение линейных объектов
• контур (замкнутая линия);
• полигон (ареал, район) - группы примыкающих друг к другу замкнутых участков (Рис. 2.6).
Рис. 2.6 Отображение полигональных объектов.
В некоторых системах в описание основных типов моделей включа-
ют понятие пространственная сеть, которая является развитием типа
данных район. Контуры и линии часто объединяют общим термином -
"линейные объекты". Таким образом, в разных ГИС число основных
типов координатных моделей меняется от трех до пяти. Проводя сравне-
ние с технологиями САПР, отметим, что основные типы координатных
данных являются аналогами атомарных моделей в САПР, которые назы-
вают примитивами.
Приведенные выше понятия носят концептуальный характер. На
практике для построения реальных объектов используют большее чис-
ло составных координатных моделей. В разных ГИС они незначительно
отличаются, поэтому рассмотрим в качестве примера набор данных в
системе ГеоГраф:
• точка - пара координат X, Y;
• отрезок - линия, соединяющая две точки;
• вершина (вертекс) - начальная или конечная точка отрезка;
• дуга (линия) - упорядоченный набор связных отрезков (или вершин);
• узел - начальная или конечная вершина дуги;
• висячий узел - узел, принадлежащий только одной дуге, у которой
начальная и конечная вершины не совпадают;
• псевдоузел - узел, принадлежащий только двум дугам либо одной замкнутой дуге, у которой начальная и конечная вершины совпадают. Исключением является узел, принадлежащий двум дугам, одна из которых самозамкнута в этом узле, а другая примыкает к ней (такой узел является нормальным);
• нормальный узел - узел, принадлежащий трем (и более) дугам.
Нормальным также является узел, принадлежащий двум дугам, одна из
которых самозамкнута в этом узле, а другая примыкает к ней;
• висячая дуга - дуга, имеющая висячий узел;
• замкнутая дуга - дуга, у которой совпадают начальная и конечная
вершины (у такой дуги имеется только один узел);
• полигон - единичная область, ограниченная (находящаяся внутри)
замкнутой дугой или упорядоченным набором связных дуг, которые об-
разуют замкнутый контур;
• покрытие - набор файлов, фиксирующий в виде цифровых запи-
сей пространственные объекты (точки, дуги, полигоны) и структуру
отношений между ними;
• пустое покрытие - покрытие, в котором отсутствуют простран-
ственные объекты;
• слой - покрытие, рассматриваемое в контексте его содержатель-
ной определенности (растительность, рельеф, административное деле-
ние и т.п.) или его статуса в среде редактора (активный слой, пассивный
слой);
• внутренний идентификатор пространственного объекта - целое чис-
ло, являющееся служебным идентификатором системы (уникальное для
каждого объекта данного покрытия и назначаемое автоматически в процес-
се работы редактора). Может изменяться системой в процессе работы;
• пользовательский идентификатор (внутренний ключ) простран-
ственного объекта - целое число, служащее для связи объектов цифро-
вой карты с базой (таблицами) тематических данных. Назначается и из-
меняется только пользователем.
Точечные объекты. Простейший тип пространственного объекта задают точечные данные, к которым относятся не только точки, но и все точечные условные знаки. Выбор объектов, представляемых в виде точек, зависит от масштаба карты или исследования. Например, на крупно масштабной карте точками показываются отдельные строения, а намелкомасштабной карте - города.
Особенность точечных объектов состоит в том, что они хранятся и в
виде графических файлов, как другие пространственные объекты, и в
виде таблиц, как атрибуты. Последнее обусловлено тем, что координаты
каждой точки описывают как два дополнительных атрибута. В силу это-
го информацию о наборе точек можно представить в виде развернутой
таблицы или таблицы, содержащей помимо координат наборы атрибу-
тов (идентификационные номера, тематические характеристики и т.д.).
В таких таблицах каждая строка соответствует точке - в ней собрана вся
информация о данной точке. Каждый столбец - это признак, содержащий
типизированные данные: координаты или атрибуты. Каждая точка незави-
сима от всех остальных точек, представленных отдельными строками.
Линейные объекты. Они широко применяются для описания се-
тей, для которых в отличие от точечных объектов характерно присут-
ствие топологических признаков.
Любая сеть состоит из узлов (вершин) - соединений, концов обо-
собленных линий и звеньев (дуг) - цепей в модели базы данных.
Для каждого узла существует специальная характеристика, называ-
емая валентностью, определяемая количеством звеньев в нем. Концы
обособленных линий одновалентны. Для уличных сетей (пересечения
типа "крест") наиболее характерны четырехвалентные узлы. В гидроло-
гии чаще всего встречаются трехвалентные узлы.
В древовидной сети (Е-дерево) каждая пара узлов имеет лишь одно
соединение, не допускаются петли и замкнутые контуры, большая часть
речных сетей имеет древовидную структуру.
Линейные объекты, как и точечные, имеют свои атрибуты, причем
разные для дуг (звеньев) и узлов. Атрибутами для дуг являются:
• направление движения, интенсивность движения, протяженность;
• количество полос, время пути вдоль звена;
• диаметр трубы, направление движения газа;
• напряжение в ЛЭП, высота опор;
• количество путей, уклон, ширина тоннеля, грузоподъемность и др.
Атрибуты для узла:
• наличие перехода, названия пересекающихся улиц;
• наличие автоматического регулирования перекрестков;
• тип (ручной или автоматический) перевода стрелок;
• характеристики трансформаторов ЛЭП;
• мощность компрессора.
Некоторые атрибуты (например, названия пересекающихся улиц)
служат для связи одного типа объектов с другими (узлы со звеньями),
другие характеризуют только участки звеньев сети.
Во многих ГИС для включения дополнительных атрибутов в сеть необходимо разбиение существующих звеньев и создание новых узлов. Например, звено улицы, часть которой ремонтируется, разрывается на
месте начального и конечного участка ремонта, его атрибуты присваи-
ваются новому (двухвалентному) узлу. Другой пример: для отрезка до-
роги, проходящей через мост, создаются новое звено и два новых узла.
Такой подход может привести к появлению недопустимо большого чис-
ла звеньев и двухвалентных узлов, поэтому он имеет ограничение, оп-
ределяемое ресурсами конкретной ГИС.
Сети часто используют как системы линейной адресации. В этих
случаях точки размещают в сети по данным о номере звена и о расстоя-
нии от его начала. Это более удобно, чем использовать X, Y координаты
точки из таблицы, поскольку такие данные непосредственно указывают
положение точки в сети.
Данный подход определяет метод присвоения атрибутов отдельным
участкам звеньев. При этом линейные объекты (здания, тоннели) хра-
нятся в отдельных таблицах, а с сетью они увязаны путем указания но-
мера звена и расстояния от его начала.
Для точечных объектов необходимо указать одно значение коорди-
нат, для линейных — два (для начальной и конечной точек). Это позволя-
ет при необходимости рассчитать X, Y координаты этих объектов и ис-
ключает необходимость дробить звенья и вводить двухвалентные узлы.
Ареалы. В настоящее время в ГИС может быть представлено не-
сколько типов ареалов: зоны в приложении к окружающей среде или
природным ресурсам, социально-экономические зоны, данные об уго-
дьях и др.
Для ареальных объектов границы могут определяться свойством или
явлением, а также независимо от явления (затем перечисляются значе-
ния атрибутов). Кроме того, границы могут устанавливаться искусст-
венно, например для микрорайонов.
Взаимосвязи между координатными моделями
В общем случае пространственные данные могут иметь большое число разнообразных связей. Эти связи играют важную роль для пространственного анализа данных. Например, связь типа "содержится в" позволяет соотносить объекты с их окружением, связь "пересекает" между двумя линиями важна для анализа маршрутов в сетях.
Взаимосвязи могут существовать между объектами одного типа или разных типов.
Исходя из критерия построения моделей можно выделить три основных типа взаимосвязей между координатными объектами.
Первый тип - взаимосвязи для построения сложных объектов из
ростах элементов, например, взаимосвязи между дугой и упорядочен-
ным набором определяющих ее вершин, взаимосвязи между полигоном
упорядоченным набором определяющих его линий. При этом исполь-
уют процедуры агрегации и обобщения.
Второй тип - взаимосвязи, которые можно вычислить по коорди-
натам объектов. Например, координаты точки пересечения двух линий
определяют взаимосвязь типа "скрещивается" и наличие четырехвален-
тного узла. Табличные координаты отдельной точки и данные о грани-
цax полигонов позволяют найти полигон, включающий данную точку.
Этим определяется взаимосвязь типа "содержится в". Используя данные о
раницах полигонов, можно выяснить, перекрываются ли полигоны, и тем
амым установить взаимосвязь типа "перекрывает". Другими словами, вто-
ой тип связи содержится в атрибутивных данных в неявном виде.
Третий тип - "интеллектуальный". Эти взаимосвязи нельзя вы-
числить по координатам, они должны получать специальное описание и
семантику при вводе данных. Например, можно вычислить пересечение
двух линий, но, если этими линиями являются автодороги, нельзя ска-
зать, пересекаются они или в этом месте находится развязка автодорог.
Следовательно, для решения дополнительных задач необходима инфор-
мация о связях. Учет связей происходит при кодировании данных, т.е. в
подсистемах семантического моделирования.
Номенклатура и разграфка топографических карт
Поскольку основой интеграции данных в ГИС является географическая информация, необходимо рассмотреть понятия разграфка и номенклатура топографических карт.
Разграфкой называется разделение топографических карт на листы.
Номенклатура - это система обозначений отдельных листов топографических карт.
Общегеографические карты делятся на три вида:
• обзорные (масштаб 1: 1 000 000 и мельче);
• обзорно-топографические (масштаб 1: 100 000- 1: 1 000 000);
• топографические (масштаб 1: 100 000 и крупнее).
Обзорно-топографические карты составляются по картам более крупных масштабов.
Топографические карты составляются по результатам съемок территорий и отличаются детальностью изображения местности. Это многолистные карты, т.е. на каждом листе отображается часть территории, а в совокупности на всех листах содержится полное отображение. Строго говоря, криволинейная часть поверхности отображаемой на листе карты соответствует некоей криволинейной трапеции. Поэтому для обозначения определенных листов карты используют термин трапеция.
В основу разграфки топографических карт положен лист карты масштаба 1: 1 000 000. Для составления карты такого масштаба изображение земной поверхности разбивается на 60 колонн (двухугольников) начиная от Гринвичского меридиана через 6°.
Двухугольники нумеруются арабскими цифрами от 1 до 60 на восток от 180°. Возможна нумерация от 0°. В этом случае двухугольники называют не колоннами, а зонами. Нумерация зон от колонн отличается на 30 единиц, например, колонна с номером 40 соответствует зоне с номером 10.
Таким образом колонны и зоны делят земной шар по меридианам. Параллелями через 4° по широте изображение земной поверхности делится на ряды, обозначаемые буквами латинского алфавита к северу и югу от экватора. Таким делением по меридианам и параллелям определяется номенклатура листа карты масштаба 1: 1 000 000 (миллионной).
Номенклатура каждого листа включает букву ряда и номер колонны. Так, лист, на котором показывается г. Москва, имеет номенклатуру N-37, что соответствуют 52 - 56° широты и 36 - 42° долготы. Номенклатура сдвоенных или счетверенных листов карты складывается из обозначений широтного пояса и соответственно двух или четырех колонн.
Номенклатура листов карт более крупных масштабов связана с номенклатурой листов миллионной карты. Так, лист карты масштаба
500 000 составляет 1/4 листа миллионной карты и обозначается добавлением прописной буквы А, Б, В, Г к номенклатуре листа
миллионной карты, например N-37-Б.
Лист карты масштаба 1: 300 000 составляет 1/9 листа миллионной
карты и обозначается римскими цифрами от I до IX, расположенными
перед номенклатурой миллионного листа, например I-N-37.
Лист карты масштаба 1: 200 000 составляет 1/36 листа
миллионной карты и обозначается римскими цифрами от I до XXXVI,
расположенными после номенклатуры миллионного листа, например
N-37-I.
Лист карты масштаба 1: 100 000 составляет 1/144 листа миллионной карты и обозначается арабскими цифрами от 1 до 144, расположенными после номенклатуры миллионного листа, например N-37-143.
Номенклатура листов карт более крупных масштабов строится на
основе листа карты масштаба 1: 100 000, подобно тому, как строились
номенклатуры рассмотренных выше карт на основе листа миллионной
карты.
Так, лист карты масштаба 1: 50 000 составляет 1/4 листа карты мас-
штаба 1: 100 000 и обозначается добавлением прописной буквы А, Б, В,
Г к номенклатуре листа карты стотысячного масштаба, например N-37-144-A.
Лист карты масштаба 1: 50 000 содержит 4 листа карты масштаба 1: 25 000, которые обозначаются добавлением строчных букв а, б, в, г к номенклатуре листа карты пятидесятитысячного масштаба, например N-37-144-E-6.
Лист карты масштаба 1: 25 000 содержит 4 листа карты масштаба
1: 10 000, которые обозначаются добавлением арабских цифр 1, 2, 3, 4
к номенклатуре листа карты двадцатипятитысячного масштаба, например N-37-144-B-a-l.
Лист карты масштаба 1: 100 000 содержит 256 листов карты масш-
таба 1: 5 000, которые обозначаются добавлением арабских цифр от
1 до 256 к номенклатуре листа карты стотысячного масштаба, например N-37-144-(255).
Номенклатура листа карты масштаба 1:2 000 образуется на основе деления листа карты 1: 5 000 на 9 частей. Каждый лист обозначается путем добавления строчных букв русского алфавита а, б, в, г, д, е, ж, з, и к номенклатуре пятитысячного масштаба, например N-37-144-(256-a).
2.2 АТРИБУТИВНАЯ ИНФОРМАЦИЯ В ГИС
Одних координатных данных недостаточно для описания картографической или сложной графической информации. Картографические
объекты кроме метрической обладают некоторой присвоенной им описательной информацией (названия политических единиц, городов и рек). Характеристики объектов, входящие в состав этой информации, называют атрибутами. Совокупность возможных атрибутов определяет класс атрибутивных моделей ГИС.
Выше отмечалось, что атрибутивные данные описывают тематические и временные характеристики. Таблица, содержащая атрибуты объектов, называется таблицей атрибутов.
Атрибуты, соответствующие тематической форме данных и определяющие различные признаки объектов, также хранятся в таблицах. Каждому объекту соответствует строка таблицы, каждому тематическому
признаку - столбец таблицы. Каждая клетка таблицы отражает значение
определенного признака для определенного объекта.
Временная характеристика может отражаться несколькими способами:
• путем указания временного периода существования объектов;
• путем соотнесения информации с определенными моментами времени;
• путем указания скорости движения объектов.
В зависимости от способа отражения временной характеристики она
может размещаться в одной таблице или в нескольких таблицах атрибутов данного объекта для различных временных этапов.
Применение атрибутов позволяет осуществлять анализ объектов базы
данных с использованием стандартных форм запросов и разного рода
фильтров, а также выражений математической логики. Последнее эффективно при тематическом картографировании.
Кроме того, с помощью атрибутов можно типизировать данные и
упорядочивать описание для широкого набора некоординатных данных.
Таким образом, атрибутивное описание дополняет координатное,
совместно с ним создает полное описание моделей ГИС и решает зада-
чи типизации исходных данных, что упрощает процессы классификации и обработки.
Атрибутами могут быть символы (названия), числа (статистическая
информация, код объекта) или графические признаки (цвет, рисунок,
заполнения контуров).
Числовые значения в ГИС могут относиться как к координатным
данным, так и к атрибутивным. Для пояснения этого напомним, что ос-
новной формой представления атрибутивных данных в БД является таб-
лица, а в таблице могут храниться как координаты объектов (координат-
ные данные), так и описательные характеристики (атрибутивные
данные).
Можно по-разному организовывать взаимосвязь координатного и
атрибутивного описания. Например, В. Вебером было предложено спе-
цифическое сочетание координатного и атрибутивного классов для опи-
сания картографических данных. Для построения общей модели дан-
ных ГИС он вводит четырехмерное пространство объекта, где первые
два (плановые) размера присваиваются данным X, У, атрибуты распола-
гаются в третьем измерении, а четвертое измерение резервируется для
временных наборов данных.
Такой подход не нов, он заимствован из методов релятивистской
механики и теории N-мерных пространств. По Веберу, данные по коор-
динате Z следует обрабатывать как атрибуты, помещая их в одну и ту же
категорию наряду с описательными текстами и значениями.
Существуют различные методы хранения атрибутивной информа-
ции в ГИС:
- хранение для всех объектов системы 1-2 стандартных атрибутов;
• хранение таблицы атрибутов, связанных с пространственными
объектами, и информации о реляциях;
• хранение ссылок на элементы данных иерархической или сетевой БД;
· хранение атрибутивной информации может вообще не применять-
ся, если система опирается на классификатор.
Вопросы точности координатных и атрибутивных данных
Использование любой информации допустимо, если она удовлетво-
ряет определенным критериям и стандартам. Одним из критериев при-
менимости пространственно-временных данных в системах ГИС является точность - близость результатов, расчетов или оценок к истинным значениям (или значениям, принятым за истинные). Например, точность горизонтали в цифровой базе данных, полученной на основе дигитализации по карте, можно оценить сравнением ее с горизонталью на исходной карте.
Рассмотрим несколько показателей точности в ГИС' точность вы-
числения, точность измерения, точность представления
Точность вычисления определяется количеством значимых цифр
после запятой, точность измерении - количеством значимых цифр при
измерениях, точность представления - количеством разрядов, описы-
вающих координатные данные
Точность вычислений и измерений не адекватна точности представ-
ления. Большое количество значимых цифр не всегда гарантирует точ-
ность вычислений или измерений.
Точность вычисления в ГИС велика, обычно она намного выше, чем
точность самих данных Более того, набор специальных методов и алго-
ритмов в ряде случаев позволяет повысить точность первичных измере-
ний.
Точность входит в комплекс данных, определяющий важный пока-
затель- качество данных.
В США разработаны национальные стандарты для цифровых кар-
тографических данных, которые применяются при оценке точности циф-
ровых данных.
Стандарт выделяет несколько компонентов качества данных
• позиционную точность;
• точность атрибутов;
• логическую непротиворечивость;
• полноту,
• происхождение.
Позиционная точность выражается степенью отклонения данных
ГИС о местоположении от истинного положения объекта на местности
Обычно точность карт приблизительно определяется толщиной линии,
или 0,4 мм Это соответствует 10 м в масштабе 1: 25 000.
Для проверки позиционной точности используют независимые бо-
лее точные источники, например карту более крупного масштаба, сис-
тему глобального позиционирования (GPS) и др.
Можно на основе известного в статистике правила "переноса оши-
бок" оценить точность, зная погрешности, вносимые различными ис-
точниками. Например, при создании цифровой модели имели место сле-
дующие погрешности-1 мм в исходном материале, 0,4 мм на карте, пред-
назначенной для цифрования, 0,1 мм при цифровании.
Точность атрибутов определяется близостью значений атрибута
к его истинной величине. Атрибуты могут со временем меняться: до-
вольно часто по сравнению с координатными данными.
В зависимости от типов данных точность атрибутов может быть из-
мерена разными способами. Для непрерывных атрибутов (поверхнос-
тей), например в полигонах Тиссена, точность выражается как погреш-
ность измерений. Для атрибутов категорий объектов, например класси-
фицированных полигонов, точность зависит от того, являются ли кате-
гории подходящими, достаточно подробными и определенными, и от
того, какова вероятность наличия в данных грубых ошибок.
Точность атрибута может быть различной в разных частях карты,
поэтому полезнее рассчитывать пространственную вариацию вероятно-
сти ошибки в классификации, чем пользоваться обобщенными статис-
тическими показателями.
Понятие логической непротиворечивости связано с непротиворе-
чивостью данных в базах данных.
В среде ГИС это понятие распространяется на внутреннюю непро-
тиворечивость структур данных и внутреннюю топологическую непро-
тиворечивость векторных данных. В частности, это определяет такие
требования, как замкнутость полигонов, уникальность идентификатора
полигона, наличие или отсутствие узлов на пересечениях дуг.
Понятие полноты (достаточности) данных связано со степенью
охвата данными множества соответствующих объектов. В зависимости
от правил отбора, генерализации и масштаба определяют число соот-
ветствующих объектов для полного описания ситуации, картографичес-
кой композиции, явления и т.п.
Несколько специфический показатель происхождение включает
сведения об источниках данных и операциях по созданию базы данных,
о методах кодирования данных, времени сбора данных, методе обработ-
ки данных, точности результатов вычислений и т.п.
2.3 ЭЛЕМЕНТЫ ЦИФРОВОЙ КОМПЬЮТЕРНОЙ КАРТОГРАФИИ
Векторные и растровые модели
Основой визуального представления данных при помощи ГИС-технологий служит так называемая графическая среда. Основу графической среды и соответственно визуализации базы данных ГИС составляют векторные и растровые модели.
В общем случае модели пространственных (координатных) данных
могут иметь векторное или растровое (ячеистое) представление, со-
держать или не содержать топологические характеристики. Этот подход
позволяет классифицировать модели по трем типам:
• растровая модель;
• векторная нетопологическая модель;
• векторная топологическая модель.
Все эти модели взаимно преобразуемы. Тем не менее при получе-
нии каждой из них необходимо учитывать их особенности. В ГИС фор-
ме представления координатных данных соответствуют два основных
подкласса моделей - векторные и растровые (ячеистые или мозаичные).
Возможен класс моделей, которые содержат характеристики как векто-
ров, так и мозаик. Они называются гибридными моделями.
В дальнейшем под терминами решетка, мозаика, элемент растра
будем понимать одно и то же. Основу такой классификации составляет
атомарная единица (пространства), содержащая представления площа-
дей линий и точек.
Векторная модель
Построение модели. Векторные модели данных строятся на векто-
рах, занимающих часть пространства в отличие от занимающих все про-
странство растровых моделей. Это определяет их основное преимуще-
ство - требование на порядки меньшей памяти для хранения и меньших
затрат времени на обработку и представление.
При построении векторных моделей объекты создаются путем со-
единения точек прямыми линиями, дугами окружностей, полилиниями.
Площадные объекты - ареалы задаются наборами линий. В векторных
моделях термин полигон (многоугольник) является синонимом слова
ареал.
Векторные модели используются преимущественно в транспортных,
коммунальных, маркетинговых приложениях ГИС. Системы ГИС, рабо-
тающие в основном с векторными моделями, получили название век-
торных ГИС.
В реальных ГИС имеют дело не с абстрактными линиями и точка-
ми, а с объектами, содержащими линии и ареалы, занимающими про-
странственное положение, а также со сложными взаимосвязями между
ними. Поэтому полная векторная модель данных ГИС отображает про-
странственные данные как совокупность следующих основных частей:
• геометрические (метрические) объекты (точки, линии и полигоны);
• атрибуты - признаки, связанные с объектами;
• связи между объектами.
Векторные модели (объектов) используют в качестве атомарной
модели последовательность координат, образующих линию.
Линией называют границу, сегмент, цепь или дугу. Основные типы
координатных данных в классе векторных моделей определяются через
базовый элемент линия следующим образом. Точка определяется как
выродившаяся линия нулевой длины, линия - как линия конечной дли-
ны, а площадь представляется последовательностью связанных между
собой сегментов.
Каждый участок линии может являться границей для двух ареалов
либо двух пересечений (узлов). Отрезок общей границы между двумя
пересечениями (узлами) имеет разные названия, которые являются си-
нонимами в предметной области ГИС. Специалисты по теории графов
предпочитают слову линия термин ребро, а для пересечения употребля-
ют термин вершина. Национальным стандартом США официально сан-
кционирован термин цепь (chain). В некоторых системах (Arclnfo,
GeoDraw) используется термин дуга.
В отличие от обычных векторов в геометрии дуги имеют свои атри-
буты. Атрибуты дуг обозначают полигоны по обе стороны от них. По
отношению к последовательному кодированию дуги эти полигоны име-
нуются левый и правый. Понятие дуги (цепи, ребра) является фундамен-
тальным для векторных ГИС.
Векторные модели получают разными способами. Один из наибо-
лее распространенных - векторизация сканированных (растровых) изоб-
ражений. Она заключается в выделении векторных объектов со скани-
рованного изображения и получении их в векторном формате.
Для векторизации необходимо высокое качество (отчетливые линии и
контуры) растровых образов. Чтобы обеспечить требуемую четкость ли-
ний, иногда приходится заниматься улучшением качества изображения.
Процесс сканирования требует незначительных затрат труда, но не-
обходимость последующей векторизации увеличивает расходы практи-
чески до уровня ручного цифрования. При векторизации возможны
ошибки, исправление которых осуществляется в два этапа:
1) корректировка растрового изображения до его векторизации;
2) корректировка векторных объектов.
Векторные модели с помощью дискретных наборов данных отображают непрерывные объекты или явления. Следовательно, можно говорить о векторной дискретизации. При этом векторное представление позволяет отразить большую пространственную изменчивость для одних районов, чем для других, по сравнению с растровым представлением, что обусловлено более четким показом границ и их меньшей зависимостью от исходного образа (изображения), чем при растровом отображении. Это типично для социальных, экономических, демографических явлений, изменчивость которых в ряде районов более интенсивна.
Некоторые объекты являются векторными по определению, напри-
мер границы соответствующего земельного участка, границы районов и
т.д. Поэтому векторные модели обычно используют для сбора данных
координатной геометрии (топографические записи), данных об админи-
стративно-правовых границах и т.п.
Особенности векторных моделей. В векторных форматах набор
данных определен объектами базы данных. Векторная модель может
организовывать пространство в любой последовательности и дает "про-
извольный доступ" к данным.
В векторной форме легче осуществляются операции с линейными и
точечными объектами, например, анализ сети - разработка маршрутов
движения по сети дорог, замена условных обозначений.
В растровых форматах точечный объект должен занимать целую
ячейку. Это создает ряд трудностей, связанных с соотношением разме-
ров растра и размера объекта.
Что касается точности векторных данных, то здесь можно говорить
о преимуществе векторных моделей перед растровыми, так как вектор-
ные данные могут кодироваться с любой мыслимой степенью точности,
которая ограничивается лишь возможностями метода внутреннего пред-
ставления координат. Обычно для представления векторных данных исполь-
зуется 8 или 16 десятичных знаков (одинарная или двойная точность).
Только некоторые классы данных, получаемых в процессе измере-
ний, соответствуют точности векторных данных. Это данные, получен-
ные точной съемкой (координатная геометрия); карты небольших учас-
тков, составленные по топографическим координатам, и политические
границы, определенные точной съемкой.
Не все природные явления имеют характерные четкие границы, ко-
торые можно представить в виде математически определенных линий.
Это обусловлено динамикой явлений или способами сбора простран-
ственной информации. Почвы, типы растительности, склоны, место оби-
тания диких животных - все эти объекты не имеют четких границ.
Обычно линии на карте имеют толщину 0,4 мм и, как часто считает-
ся, отражают неопределенность положения объекта. В растровой систе-
ме эта неопределенность задается размером ячейки. Поэтому следует помнить, что в ГИС действительное представление о точности дают раз-
мер растровой ячейки и неопределенность положения векторного объек-
та, а не точность координат.
Геометрические данные составляют основу векторной модели, тем
не менее, как отмечено выше, в ее состав входят также атрибуты и свя-
зи. Атрибуты уже рассматривались достаточно подробно. Остановимся
на связях в векторных моделях. Для этого необходимо рассмотреть то-
пологические свойства векторных моделей, т.е. рассмотреть топологи-
ческие модели, которые являются разновидностью векторных моделей
данных.
Топологическая модель
Основные понятия. Большое количество графических данных в
ГИС со специфическими взаимными связями требует топологического
описания объектов и групп объектов, которое зависит от "связанности"
(простой или сложной). Оно определяет совокупность топологических
моделей.
Напомним, что топологические свойства фигур не изменяются при
любых деформациях, производимых без разрывов или соединений. Топологически родственные фигуры: прямоугольный четырехугольник, замкнутый контур произвольной формы, окружность, треугольник. Эти объекты (фигуры) имеют одинаковую топологию - одинаковые топологические свойства. Другим примером топологически родственных фигур могут служить арифметические знак” сложения " + " и умножения " х ".
В геоинформационных системах применение термина топологический не такое строгое, как в топологии. В ГИС топологическая модель определяется наличием и хранением совокупностей взаимосвязей, таких, как соединенность дуг на пересечениях, упорядоченный набор звеньев (цепей), образующих границу каждого полигона, взаимосвязи смежности между ареалами и т.п.
В общем смысле слово топологический означает, что в модели объек-
та хранятся взаимосвязи, которые расширяют использование данных
ГИС для различных видов пространственного анализа.
Топологическими характеристиками графические модели ГИС су-
щественно отличаются от моделей САПР. Соответственно это различие
просматривается в программно-технологическом обеспечении этих си-
стем.
Например, вплоть до настоящего времени много разработок ГИС
выполняется с использованием средств Автокада, версий от 10 до 13
Однако в нем не предусмотрены ни работа с покрытиями, ни оверлей-
ные процедуры, ни обработка топологических данных. Принципиально
такие операции в системах CAD (Computer-Aided Desing) возможны, но
путем доработки программного обеспечения, что требует достаточно
высокой квалификации пользователя и, естественно, ограничивает их
круг.
В системах ГИС названные выше процедуры являются встроенны-
ми и делают доступным анализ картографической информации широ-
кому кругу пользователей без всякой доработки.
Элементы топологии, входящие в описание моделей данных ГИС, в
простейшем случае определяются связями между элементами основных
типов координатных данных. Например, в логическую структуру описания данных могут входить указания о том, какие линии входят в район, в каких точках эти линии пересекаются.
Топологические модели позволяют представлять элементы карты и
всю карту в целом в виде графов. Площади, линии и точки описываются
границами и узлами (дуговая/узловая структура). Каждая граница идет
от начального к конечному узлу, и известно, какие площади находятся
слева и справа.
Теоретической основой моделей служат алгебраическая топология
и теория графов. В соответствии с алгебраической топологией коорди-
натные типы данных: площади, линии и точки называются 2-ячейками,
1-ячейками и 0-ячейками соответственно. Карта рассматривается как
ориентированный двухмерный ячеечный комплекс.
Двойственность между теорией графов и алгебраической топологи-
ей позволяет применять теоретические положения графов, а также то-
пологический подход.
Топологическое векторное представление данных отличается от не-
топологического наличием возможности получения исчерпывающего
списка взаимоотношений между связанными геометрическими прими-
тивами без изменения хранимых координат пространственных объектов.
Необходимая процедура при работе с топологической моделью -
подготовка геометрических данных для построения топологии. Этот
процесс не может быть полностью автоматизирован уже на данных сред-
ней сложности и реализуется только при дополнительных затратах тру-
да (обычно значительных). Таким образом, данные, хранимые в систе-
ме, не предусматривающей поддержки топологии, не могут быть надежно
преобразованы в топологические данные другой системы чисто автома-
тическим алгоритмом.
Топологические характеристики должны вычисляться в ходе коли-
чественных преобразований моделей объектов ГИС, а затем храниться
в базе данных совместно с координатными данными.
Основные топологические характеристики моделей ГИС. Топо-
логические модели в ГИС задаются совокупностью следующих харак-
теристик:
• связанность векторов - контуры, дороги и прочие векторы должны
храниться не как независимые наборы точек, а как взаимосвязанные друг
с другом объекты;
• связанность и примыкание районов - информация о взаимном рас-
положении районов и об узлах пересечения районов;
• пересечение - информация о типах пересечений позволяет вос-
производить мосты и дорожные пересечения. Так Т-образ-
ное пересечение (3 линии) является трехвалентным, а Х-образное
(4 линии сходятся в точке пересечения) называют четырехвалентным;
• близость - показатель пространственной близости линейных или
ареальных объектов, оценивается числовым параметром, в
данном случае символом 5.
Топологические характеристики линейных объектов могут быть
представлены визуально с помощью связанных графов. Граф сохраняет
структуру модели со всеми узлами и пересечениями. Он напоминает
карту с искаженным масштабом. Примером такого графа может служить
схема метрополитена. Разница между картой метро и схемой метро по-
казывает разницу между картой и графом.
Узлы графа, описывающего картографическую модель, соответству-
ют пересечениям дорог, местам смыкания дорог с мостами и т.п. Ребра
такого графа описывают участки дорог и соединяющие их объекты. В
отличие от классической сетевой модели в данной модели длина ребер
может не нести информативной нагрузки.
Топологические характеристики ареальных объектов могут быть представлены с помощью графов покрытия и смежности. Граф покрытия топологически гомоморфен контурной карте соответствующих районов. Ребра такого графа описывают границы между районами, а его узлы (вершины) представляют точки смыкания районов. Степень вершины такого графа - это число районов, которые в ней смыкаются. Граф смежности это как бы вывернутый наизнанку граф покрытия. В нем районы отображаются узлами (вершинами), а пара смыкающихся районов ребрами. На основе такого графа ГИС может выдать ответ на вопрос, является ли проходимой рассматриваемая территория, разделенная напроходимые или непроходимые участки.
Топологические характеристики сопровождаются позиционной и описательной информацией. Вершина графа покрытия может быть дополнена координатными точками, в которых смыкаются соответствующие районы, а ребрам приписывают левосторонние и правосторонние идентификаторы.
После введения точечных объектов при построении линейных и
площадных объектов необходимо "создать" топологию. Эти процессы
включают вычисление и кодирование связей между точками, линиями и
ареалами.
Пересечения и связи имеют векторное представление. Топологичес-
кие характеристики заносятся при кодировании данных в виде дополни-
тельных атрибутов Этот процесс осуществляется автоматически во многих ГИС в ходе дигитализации (картографических или фотограмметрических) данных.
Объекты связаны множеством отношений между собой. Это определяет эффективность применения реляционных моделей и баз данных, в основе которых используется понятие отношения. В свою очередь, отношения задают множества связей. Простейшие примеры таких связей: "ближайший к.. ", "пересекает", "соединен с...".
Каждому объекту можно присвоить признак, который представляет
собой идентификатор ближайшего к нему объекта того же класса; таким
образом кодируются связи между парами объектов.
В ГИС часто кодируются два особых типа связей: связи в сетях и
связи между полигонами.
Топологически сети состоят из объектов двух типов: линий (звенья,
грани, ребра, дуги) и узлов (вершины, пересечения, соединения).
Простейший способ кодирования связей между звеньями и узлами зак-
лючается в присвоении каждому звену двух дополнительных атрибутов -
идентификаторов узлов на каждом конце (входной узел и выходной узел).
В этом случае при кодировании геометрических данных будут иметь
место два типа записей:
1) координаты дуг;
2) атрибуты дуг - входной узел, выходной узел, длина, описательные характеристики.
Такая структура позволяет, перемещаясь от звена к звену, определять те из них, у которых перекрываются номера узлов.
Более сложная, но и более совершенная структура имеет список всех звеньев для каждого узла. Это может быть выполнено добавлением к первым двум записи третьего типа;
3) узел: (х, у), смежные дуги (со знаком "+" для входного угла и со знаком "-" - для выходного).
Чтобы избежать неудобств, связанных с хранением неодинакового количества идентификаторов дуг, используют два отдельных файла:
1) простой упорядоченный список, в котором файл узлов сжат до
ряда идентификаторов дуг;
2) таблицу, в которой для каждого узла хранится информация о по-
ложении первой дуги списка.
Используемое в настоящее время математическое обеспечение ГИС
почти исключительно основано на топологических моделях, дающих
хорошее формализованное представление о пространственных соотно-
шениях между основными объектами карты. Однако, если требуется
установить более сложные соотношения, например включение или по-
рядок, нужны дополнительные средства.
Растровые модели
Основы построения. Напомним, что модель данных представляет
собой отображение непрерывных последовательностей реального мира
в набор дискретных объектов.
В растровых моделях дискретизация осуществляется наиболее про-
стым способом - весь объект (исследуемая территория) отображается в
пространственные ячейки, образующие регулярную сеть. При этом каж-
дой ячейке растровой модели соответствует одинаковый по размерам,
но разный по характеристикам (цвет, плотность) участок поверхности
объекта. В ячейке модели содержится одно значение, усредняющее ха-
рактеристику участка поверхности объекта. В теории обработки изоб-
ражений эта процедура известна под названием пикселизация.
Если векторная модель дает информацию о том, где расположен тот
или иной объект, то растровая - информацию о том, что расположено в
той или иной точке территории. Это определяет основное назначение
растровых моделей - непрерывное отображение поверхности.
В растровых моделях в качестве атомарной модели используют двух-
мерный элемент пространства - пиксель (ячейка). Упорядоченная сово-
купность атомарных моделей образует растр, который, в свою очередь,
является моделью карты или геообъекта.
Векторные модели относятся к бинарным или квазибинарным Рас-
тровые позволяют отображать полутона.
Как правило, каждый элемент растра или каждая ячейка должны
иметь лишь одно значение плотности или цвета. Это применимо не для
всех случаев. Например, когда граница двух типов покрытий может про-
ходить через центр элемента растра, элементу дается значение, характе-
ризующее большую часть ячейки или ее центральную точку Ряд систем
позволяет иметь несколько значений для одного элемента растра.
Характеристики растровых моделей. Для растровых моделей су-
ществует ряд характеристик разрешение, значение, ориентация, зоны,
положение.
Разрешение - минимальный линейный размер наименьшего участ-
ка пространства (поверхности), отображаемый одним пикселем.
Пиксели обычно представляют собой прямоугольники или квадра-
ты, реже используются треугольники и шестиугольники. Более высо-
ким разрешением обладает растр с меньшим размером ячеек Высокое
разрешение подразумевает обилие деталей, множество ячеек, минималь-
ный размер ячеек
Значение - элемент информации, хранящийся в элементе растра
(пикселе) Поскольку при обработке применяют типизированные дан-
ные, то есть необходимость определить типы значений растровой мо-
дели
Тип значении в ячейках растра определяется как реальным явлением, так и особенностями ГИС. В частности, в разных системах можно
использовать разные классы значений- целые числа, действительные
(десятичные) значения, буквенные значения
Целые числа могут служить характеристиками оптической плотно-
сти или кодами, указывающими на позицию в прилагаемой таблице или
легенде Например, возможна следующая легенда, указывающая наиме-
нование класса почв- 0 - пустой класс, 1 - суглинистые, 2 - песчаные,
3 - щебнистые и т. п.
Ориентация - угол между направлением на север и положением
колонок растра
Зона растровой модели включает соседствующие друг с другом
ячейки, имеющие одинаковое значение Зоной могут быть отдельные
объекты, природные явления, ареалы типов почв, элементы гидро-
графии и т. п.
Для указания всех зон с одним и тем же значением используют по-
нятие класс зон Естественно, что не во всех слоях изображения могут
присутствовать зоны. Основные характеристики зоны - ее значение и
положение
Буферная зона - зона, границы которой удалены на известное расстояние от любого объекта на карте Буферные зоны различной ширины могут быть созданы вокруг выбранных объектов на базе таблиц сопряженных характеристик.
Положение обычно задается упорядоченной парой координат (но-
мер строки и номер столбца), которые однозначно определяют положе-
ние каждого элемента отображаемого пространства в растре.
Проводя сравнение векторных и растровых моделей, отметим удобство
векторных для организации и работы со взаимосвязями объектов. Тем не
менее, используя простые приемы, например включая взаимосвязи в таб-
лицы атрибутов, можно организовать взаимосвязи и в растровых системах..
Необходимо остановиться на вопросах точности отображения в ра-
стровых моделях. В растровых форматах в большинстве случаев неяс
но, относятся координаты к центральной точке пикселя или к одному из
его углов. Поэтому точность привязки элемента растра определяют как
1/2 ширины и высоты ячейки.
Растровые модели имеют следующие достоинства:
• растр не требует предварительного знакомства с явлениями, дан-
ные собираются с равномерно расположенной сети точек, что позволя-
ет в дальнейшем на основе статистических методов обработки получать
объективные характеристики исследуемых объектов Благодаря этому
растровые модели могут использоваться для изучения новых явлений, о
которых не накоплен материал. В силу простоты этот способ получил
наибольшее распространение;
• растровые данные проще для обработки по параллельным алго-
ритмам и этим обеспечивают более высокое быстродействие по сравне-
нию с векторными;
• некоторые задачи, например создание буферной зоны, много про-
ще решать в растровом виде;
• многие растровые модели позволяют вводить векторные данные, в
то время как обратная процедура весьма затруднительна для векторных
моделей;
• процессы растеризации много проще алгоритмически, чем про-
цессы векторизации, которые зачастую требуют экспертных решений.
Наиболее часто растровые модели применяют при обработке аэро-
космических снимков для получения данных дистанционных исследо-
ваний Земли.
Метод группового кодирования. При растровом вводе информации в ГИС возникает проблема ее сжатия, так как наряду с полезной может попадать и избыточная (в том числе и бесполезная) информация. Для сжатия информации, полученной со снимка или карты, применяется кодирование участков развертки или метод группового кодирования, учитывающий, что довольно часто в нескольких ячейках значения повторяются.
Суть метода группового кодирования состоит в том, что данные вводятся парой чисел, первое обозначает длину группы, второе - значение.Изображение просматривается построчно, и как только определенныйтип элемента или ячейки встречается впервые, он помечается признаком начала. Если за данной ячейкой следует цепочка ячеек того же типа,то их число подсчитывается, а последняя ячейка помечается признакомконца. В этом случае в памяти хранятся только позиции помеченныхячеек и значения соответствующих счетчиков.
Применение такого метода значительно упрощает хранение и воспроизведение изображений (карт), когда однородные участки (как правило) превосходят размеры одной ячейки.
Обычно ввод осуществляют слева направо, сверху вниз. Рассмотрим, например, бинарный массив матрицы (5х6):
001110
001110
011111
011111.
При использовании метода группового кодирования он будет вводиться как: 30312031303120511051.
Вместо 30 необходимо только 20 элементов данных. В рассмотренном примере экономия составляет 30 %, однако на практике при работе с большими массивами бинарных данных она бывает гораздо больше.
Метод группового кодирования имеет ограничения и может использоваться далеко не во всех ГИС.
Элементы бинарной матрицы, т.е. растровой модели, могут принимать только два значения: "1" или "0". Эта матрица соответствует черно-белому изображению. На практике возможно полутоновое или цветное изображение. В этих случаях значения в ячейках растровой модели могут различаться по типам. Тип значений в ячейках растра определяется как исходными данными, так и особенностями программных средств ГИС. В качестве значений растровых данных могут быть применены целые числа, действительные (десятичные) значения, буквенные значения.
В одних системах используются только целые числа, в других - раз-
личные типы данных. При этом ставится условие единства значений для
отдельных растровых слоев. Целые числа часто служат кодами, указы-
вающими на позицию в прилагаемой таблице или легенде.
Структурно определенные растровые модели. Растровые модели делятся на регулярные, нерегулярные и вложенные (рекурсивные или иерархические) мозаики.
Плоские регулярные мозаики бывают трех типов: квадрат, треугольник и шестиугольник. Квадрат - самая удобная модель, так как позволяет относительно просто проводить обработку больших массивов данных. Треугольные мозаики служат
