Указания к выполнению задания

УДК 514.18(076)

ББК 22.151.ЗЯ7

 

 

Рецензент

В.В. Смагин - доцент, канд. техн. наук

 

Составители: В.Г. Середа¹, А.Ф. Медведь²

 

Моделирование метрических характеристик объектов: метод. указания / сост. В.Г. Середа¹, А.Ф. Медведь². – Севастополь: СевГУ, 2016. – 20 с.:ил.

 

Методические указания составлены в соответствии с рабочей программой дисциплины «Начертательная геометрия и инженерная графика» на основании государственного образовательного стандарта высшего профессионального образования.

В указаниях приведены фрагменты теории, варианты индивидуальных заданий, образцы выполненных заданий с примерами их пошагового выполнения.

Методические указания предназначены для студентов технических специальностей дневной и заочной формы обучения.

 

Рекомендовано Учебно-методическим советом института в качестве методических указаний по дисциплине «Начертательная геометрия и инженерная графика» для студентов технических специальностей дневной и заочной формы обучения.

 

 

УДК 514.18(076)

 

© Середа В.Г.¹,

Медведь А.Ф. ², сост., 2016

© ФГАОУВО «Севастопольский

государственный университет», 2016

СОДЕРЖАНИЕ

ВВЕДЕНИЕ
1. Цель и содержание задания
2. Указания к выполнению задания
3. Фрагменты теории
4. Пошаговое выполнение задания
4.1. Пример решения задачи 1
4.2. Пример решения задачи 2
4.3. Пример решения задачи 3
4.4. Пример решения задачи 4
ЗАКЛЮЧЕНИЕ
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ЛИТЕРАТУРЫ

ВВЕДЕНИЕ

К элементарным метрическим задачам относятся задачи на определение расстояний и углов между парами геометрических элементов (точкой, прямой и плоскостью).

Возможны два пути решения элементарных метрических задач:

– без преобразования комплексного чертежа;

– с преобразованием комплексного чертежа (решение проще и поэтому рекомендуется в данном задании).

Преобразование комплексного чертежа – это процесс построения дополнительных изображений объекта по его основным проекциям. В основе преобразования комплексного чертежа лежит перевод (перемещение) объекта из общего положения в частное, т.е. удобное для решения задачи. Это достигается двумя путями:

– изменением положения объекта относительно неподвижных плоскостей проекций (способы вращения и перемещения);

– изменением положения плоскостей проекций по отношению к неподвижному объекту (способ замены плоскостей проекций).

Вариант для выполнения задания определяется как остаток от деления трех последних цифр номера зачетной книжки на 30. Например, если номер зачетной книжки студента 030231, то он выполняет 21-й вариант, так как при делении 231 на 30 в остатке будет 21. Если остаток равен нулю, то принимается 30 вариант.

 

ЦЕЛЬ И СОДЕРЖАНИЕ ЗАДАНИЯ

Цель задания – усвоение основных способов преобразования комплексного чертежа (построения дополнительных изображений) и алгоритмов решения метрических задач.

Содержание работы. Задание состоит из четырех задач.

Задача 1. Определить истинную величину основания АВС трехгранной пирамиды SАВС.

Задача 2. Определить величину расстояния от вершины S до плоскости основания АВС трехгранной пирамиды SАВС.

Задача 3. Определить расстояния между ребрами АS и ВС трехгранной пирамиды SАВС.

Задача 4. Определить истинную величину двугранного угла при ребре ВС трехгранной пирамиды SАВС.

УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЯ

 

Данные для построения комплексного чертежа взять из таблицы 1 в соответствии с вариантом. Задание выполнить на одном листе формата А3 (420х297). Образец выполнения задания приведен на рисунке 1.

Задачи должны быть решены следующими способами:

– плоско-параллельного перемещения;

 

Таблица 1 – Исходные данные (координаты точек в мм) к задачам 1,2,3,4

№ вар.

A

B

C

S

X

y

z

x

y

z

X

y

z

x

y

z

 

Рис. 1

– вращения вокруг проецирующей прямой;

– вращения вокруг линии уровня;

– замены плоскостей проекций.

Студенты могут самостоятельно выбрать наиболее рациональный способ решения каждой задачи, но так, чтобы были применены все перечисленные способы. На чертеже рекомендуется вычертить только те геометрические элементы, которые необходимы для решения поставленной задачи.

Рекомендуемая компоновка листа приведена на рисунке 2.

Задание выполняется в следующей последовательности:

1. В верхней части чертежа справа вычертить и заполнить таблицу исходных данных выбранных по варианту из таблицы 1.

2. В верхней части чертежа слева вычертить условие задачи 1 (две проекции основания пирамиды) и выполнить необходимые построения для решения задачи (см. п. 4.1).

3. Вычертить условие задачи 2 (две проекции основания и вершины пирамиды) и выполнить решение задачи (см. п. 4.2).

4. Вычертить в правой части листа условие задачи 3 (две проекции скрещивающихся ребер пирамиды) и выполнить решение задачи (см. п.4.3).

5. Вычертить внизу листа слева условие задачи 4 (две проекции двугранного угла) и выполнить решение задачи (см. п. 4.4).

6. Обвести чертеж линиями в соответствии с ГОСТ 2.303-68 и заполнить основную надпись (ГОСТ 2.104-68).

Для решения первой задачи следует преобразовать комплексный чертеж так, чтобы плоскость основания пирамиды стала плоскостью уровня.

Для решения второй задачи следует преобразовать комплексный чертеж так, чтобы плоскость основания пирамиды стала проецирующей плоскостью.

Для решения третьей задачи следует преобразовать комплексный чертеж так, чтобы одно из ребер пирамиды стало проецирующим.

Для решения четвертой задачи следует преобразовать комплексный чертеж так, чтобы общее ребро двугранного угла стало проецирующим.

 

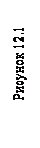3. ФРАГМЕНТЫ ТЕОРИИ

Между парами геометрических элементов можно составить одиннадцать метрических задач:

Задача 1. Определить кратчайшее расстояние между двумя точками.

Задача 2. Определить кратчайшее расстояние между точкой и плоскостью.

Задача 3. Определить кратчайшее расстояние между прямой и параллельной ей плоскостью.

Задача 4. Определить кратчайшее расстояние между двумя параллельными плоскостями.

Задача 5. Определить кратчайшее расстояние между точкой и прямой.

Задача 6. Определить кратчайшее расстояние между двумя параллельными прямыми.

Задача 7. Определить кратчайшее расстояние между двумя скрещивающимися прямыми.

Задача 8. Определить величину угла между двумя пересекающимися прямыми.

Задача 9. Определить величину угла между двумя скрещивающимися прямыми.

Задача 10. Определить величину угла между двумя пересекающимися плоскостями.

Задача 11. Определить величину угла между прямой и плоскостью.

Решение любой элементарной задачи с преобразованием комплексного чертежа состоит из трех операций:

1) мысленно представить отрезок или плоский угол, с помощью которых измеряется искомое расстояние или величина угла;

Рис. 2

 

2) мысленно определить положение объекта относительно плоскости проекций, при котором отрезок или плоский угол проецируются в натуральную величину;

3) вычертить дополнительную проекцию объекта и на ней измерить искомое расстояние или величина угла.

Анализ решений всех одиннадцати элементарных метрических задач показывает, что существует четыре решающих положения (положение объекта относительно плоскости проекций, при котором отрезок или плоский угол, используемый для определения расстояния или величины угла, проецируется в натуральную величину):

1) положение, при котором заданная прямая объекта становится линией уровня;

2) положение, при котором заданная прямая объекта становится проецирующей прямой;

3) положение, при котором заданная плоскость объекта становится проецирующей плоскостью;

4) положение, при котором заданная плоскость объекта становится плоскостью уровня.

При решении задач с помощью преобразования комплексного чертежа выделяют четыре типовых построения, которые называют конструктами (основными задачами).

Конструкт 1. Преобразование прямой общего положения в прямую уровня.

Конструкт 2. Преобразование прямой уровня в проецирующую прямую.

Конструкт 3. Преобразование плоскости общего положения в проецирующую плоскость.

Конструкт 4. Преобразование проецирующей плоскости в плоскость уровня.

Приведем краткие (свернутые) формулировки алгоритмов решения одиннадцати элементарных метрических задач:

– для решения задачи 1 следует преобразовать комплексный чертеж так, чтобы отрезок, соединяющий две точки, стал линией уровня (конструкт 1);

– для решения задачи 2 следует преобразовать комплексный чертеж так, чтобы заданная плоскость стала проецирующей (конструкт 3);

– для решения задачи 3 следует преобразовать комплексный чертеж так, чтобы заданная плоскость стала проецирующей (конструкт 3);

– для решения задачи 4 следует преобразовать комплексный чертеж так, чтобы заданные плоскости стали проецирующими (конструкт 3);

– для решения задачи 5 следует преобразовать комплексный чертеж так, чтобы заданная прямая стала проецирующей прямой (конструкт 2);

– для решения задачи 6 следует преобразовать комплексный чертеж так, чтобы заданные прямые стали проецирующими (конструкт 2);

– для решения задачи 7 следует преобразовать комплексный чертеж так, чтобы одна из заданных прямых стала проецирующей прямой (конструкт 2);

– для решения задачи 8 следует преобразовать комплексный чертеж так, чтобы плоскость определяемая пересекающимися прямыми стала плоскостью уровня (конструкт 4);

– для решения задачи 9 следует преобразовать комплексный чертеж так, чтобы плоскость, проходящая через одну из прямых и параллельная другой прямой, стала проецирующей (конструкт 3);

–.для решения задачи 10 следует преобразовать комплексный чертеж так, чтобы обе плоскости стали проецирующими (конструкт 3);

–. для решения задачи 1 следует преобразовать комплексный чертеж так, чтобы плоскость проходящая через прямую и перпендикулярная заданной плоскости стала плоскостью уровня (конструкт 4).

Основные положения начертательной геометрии, необходимые для выполнения задания приведены в таблице 2.

 

Таблица 2 – Основные графические операции, встречающиеся в индивидуальных заданиях

1. Если дополнительная плоскость проекций перпендикулярна незаменяемой плоскости проекций, то новая проекция точки лежит на линии связи, проходящей через незаменяемую проекцию точки перпендикулярно новой оси проекций и имеет координату замененной проекции точки (основа способа замены плоскостей проекций).

2. Если объект вращается вокруг оси, перпендикулярной плоскости проекций, то проекции точек объекта, одноименные с вырожденной проекцией оси, перемещаются по концентрическим окружностям, сохраняя форму и размеры проекции объекта, а точки второй его проекции перемещаются параллельно оси проекций (основа способа вращения вокруг проецирующей прямой).

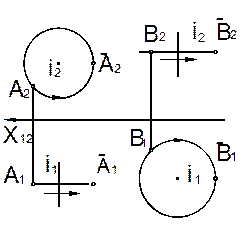Продолжение таблицы 2

3. Если точки объекта перемещаются в плоскостях уровня, то проекции точек на одной из плоскостей проекций перемещаются произвольно, сохраняя расстояния между собой, а на другой – параллельно оси проекций (основа способа плоскопараллельного перемещения), который является частным случаем способа вращения вокруг проецирующей прямой).	4. Если точки объекта поворачиваются вокруг линии уровня, то проекции точек, одноименные с неискаженной проекцией оси вращения, перемещаются по вырожденным проекциям плоскостей вращения точек, перпендикулярно неискаженной проекции оси вращения, а точки другой проекции – по эллипсу (основа способа вращения вокруг линии уровня).
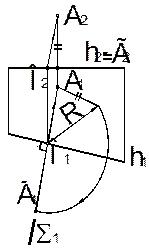
5. Если новая плоскость проекций параллельна прямой общего положения, то новая ось проекций параллельна одной из проекций этой прямой (преобразование прямой общего положения в прямую уровня).	6. Если дополнительная плоскость проекций перпендикулярна прямой уровня, то новая ось проекций перпендикулярна неискаженной проекции этой прямой (преобразование прямой уровня в проецирующую прямую).

 

Продолжение таблицы 2

7. Если дополнительная плоскость проекций перпендикулярна плоскости общего положения, то новая ось проекций перпендикулярна неискаженной проекции прямой уровня плоскости (преобразование плоскости общего положения в проецирующую плоскость).	8. Если дополнительная плоскость проекций параллельная проецирующей плоскости, то новая ось проекций параллельна вырожденной проекции плоскости (преобразование проецирующей плоскости в плоскость уровня).
9. Если прямую общего положения повернуть вокруг проецирующей прямой до положения параллельного плоскости проекций, то одна её проекция займет положение, параллельное оси проекций (преобразование прямой общего положения в прямую уровня).	10. Если прямую уровня повернуть вокруг одноименной проецирующей прямой до положения перпендикулярного плоскости проекций, то неискаженная проекция отрезка прямой займет положение, перпендикулярное оси проекций (преобразование прямой уровня в проецирующую прямую).

 

Продолжение таблицы 2

11. Если плоскость общего положения повернуть вокруг проецирующей прямой до положения перпендикулярного плоскости проекций, то неискаженная проекция линии уровня займет положение, перпендикулярное оси проекций (преобразование плоскости общего положения в проецирующую плоскость).	12. Если проецирующую плоскость повернуть вокруг одноименно проецирующей прямой (оси вращения) до положения плоскости, параллельной плоскости проекций, то её вырожденная проекция займет положение, параллельное оси проекций (преобразование проецирующей плоскости в плоскость уровня).
13. Если одну из проекций прямой общего положения плоско-параллельно переместить без изменения размеров и формы в положение параллельное оси проекций Х, то другая проекция прямой будет равна истинной величине отрезка прямой (преобразование прямой общего положения в прямую уровня).	14. Если неискаженную проекцию отрезка прямой плоско-параллельно переместить без изменения размеров и формы в положение перпендикулярное оси проекций Х, то вторая его проекция выродится в очку (преобразование прямой уровня в проецирующую прямую).

 

Продолжение таблицы 2

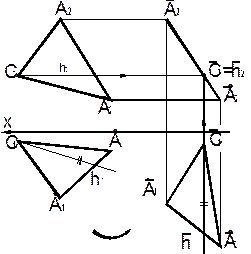
15. Если проекцию плоскости с неискаженной проекцией линии уровня плоско-параллельно переместить без изменения размеров и формы в положение, при котором линия уровня будет перпендикулярна оси Х, то вторая проекция плоскости выродится в отрезок прямой (преобразование плоскости общего положения в проецирующую плоскость).	16. Если вырожденную проекцию плоскости плоско-параллельно переместить без изменения размеров и формы в положение параллельное оси Х, то другая его проекция будет равна истинной величине отсека плоскости (преобразование проецирующей плоскости в плоскость уровня).
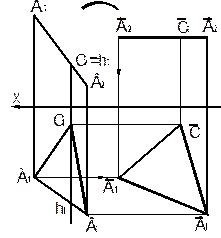
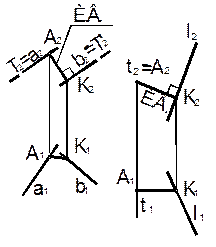
17. Расстояние между скрещивающимися прямыми проецируется в истинную величину на ту плоскость проекции, по отношению к которой их плоскости параллелизма являются проецирующими или по отношению к которой одна из прямых является проецирующей.	18. Расстояние между точкой и плоскостью проецируется в истинную величину на ту плоскость проекций, по отношению к которой плоскость является проецирующей.

 

 

Продолжение таблицы 2

19. Угол между пересекающимися или скрещивающимися прямыми проецируется в истинную величину на ту плоскость проекций, по отношению к которой эти прямые являются линиями уровня.

20. Двугранный угол между пересекающимися плоскостями проецируется в истинную величину на ту плоскость проекций, по отношению к которой линия пересечения плоскостей является проецирующей (плоскости тоже).