Определение 1.1.8. Элементарной абелевой p-группой называют группу, являющуюся прямым произведением подгрупп порядка р.
Теорема 2.3.1. Пусть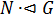 
и 
. Тогда K — простая подгруппа и существуют элементы 
такие, что 
. Кроме того:
1) если N абелева, то 
для некоторого простого р и N — элементарная абелева р-группа;
2) если N неабелева, то каждая минимальная нормальная в N подгруппа принадлежит множеству 
.
Доказательство. Пусть 
и 
. Ясно, что L является нормальной подгруппой группы G. Так как 
для всех 
, то 
, поэтому 
. Поскольку 
— минимальная нормальная подгруппа в N, то по лемме 1.2.4. существуют элементы такие, что . Из леммы 1.2.1 следует что подгруппа K простая.
1. Пусть N абелева. По теореме 6.5, с. 63, подгруппа K имеет простой порядок. Пусть 
. Тогда N — элементарная абелева p -группа порядка 
.
2. Пусть N неабелева. По теореме 1.2.3. каждая минимальная нормальная в N подгруппа принадлежит множеству .
Следствие 2.3.1. Минимальная нормальная подгруппа группы является характеристически простой группой.
Следствие 2.3.2. Минимальная нормальная подгруппа группы либо элементарная абелева р-группа для некоторого простого р, либо является прямым произведением изоморфных простых неабелевых групп. □
Лемма 2.3.1. Пусть 
, 
. Если 
, 
, то существуют элементы 
такие, что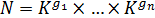 
.
Доказательство.
Так как 
для любого , то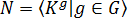 
. Полагая из леммы 1.2.4. для группы H и ее нормальной подгруппы N получаем, что существуют элементы 
такие, что .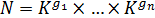
Заключение
В данном реферате были выполнены следующие задачи:
· Рассмотрены основные определения теории групп и центральные теоремы (определение группы, нормальной подгруппы, простой подгруппы, элементарной абелевой p-группы и другие; теорема Лагранжа, теорема о гомоморфизмах и другие).
· Изучены простейшие свойства минимальных нормальных подгрупп.
· Рассмотрены характеристически простые группы и их строение.
· Исследовано строение минимальных нормальных подгрупп конечных групп.
Список литературы
1. Воробьев Н.Н. Алгебра классов конечных групп. Витебск: ВГУ имени П.М. Машерова, 2012.
2. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. - М.: Наука, 1982.
3. Кострикин А. И. Введение в алгебру. Часть 1. Основы алгебры. - М.: Физико-математическая литература, 2000.
4. Кострикин А.И. Введение в алгебру. Часть 2. Линейная алгебра. - М.: Физико-математическая литература, 2000.
5. Кострикин А.И. Введение в алгебру. Часть 3. Основные структуры алгебры. - М.: Физико-математическая литература, 2000.
6. Курош А.Г. Теория групп. – М.: Физико-математическая литература, 2011.
7. Монахов В.С. Введение в теорию конечных групп и их классов: учебное пособие. – Мн.: Вышэйшая школа, 2006.
