Лабораторная работа № 1
ПЕРВИЧНАЯ ОБРАБОТКА ДАННЫХ
Цель работы: ознакомиться с основными понятиями математической статистики и методикой проведения первичного исследования статистических данных.
Задание: При проведении экспериментов фиксировались значения случайной величины X, характеризующей стоимость строительно-монтажных работ на участке, у.е.. Произвести первичную обработку полученных опытных данных с целью изучения свойств случайной величины Х.
Пример выполнения лабораторной работы №1.
1) Составим расчетную таблицу, в которой запишем вариационный ряд (элементы выборки в порядке неубывания признака) и произведем расчеты, необходимые для вычисления числовых характеристик.
Таблица 1.1 – Расчетная таблица
| Номер п/п | Выборка, у.е. | Вариацион- ный ряд, у.е., 
|

| 
| 
|

|
| -42,160 | 1777,466 | -74937,950 | 3159383,959 | |||
| -38,160 | 1456,186 | -55568,042 | 2120476,502 | |||
| -38,160 | 1456,186 | -55568,042 | 2120476,502 | |||
| -30,160 | 909,626 | -27434,308 | 827418,732 | |||
| -27,160 | 737,666 | -20034,998 | 544150,537 | |||
| -25,160 | 633,026 | -15926,924 | 400721,410 | |||
| -23,160 | 536,386 | -12422,690 | 287709,512 | |||
| -23,160 | 536,386 | -12422,690 | 287709,512 | |||
| -22,160 | 491,066 | -10882,014 | 241145,424 | |||
| -22,160 | 491,066 | -10882,014 | 241145,424 | |||
| -21,160 | 447,746 | -9474,297 | 200476,122 | |||
| -18,160 | 329,786 | -5988,906 | 108758,542 | |||
| -14,160 | 200,506 | -2839,159 | 40202,496 | |||
| -13,160 | 173,186 | -2279,122 | 29993,252 | |||
| -11,160 | 124,546 | -1389,929 | 15511,606 | |||
| -9,160 | 83,906 | -768,575 | 7040,150 | |||
| -9,160 | 83,906 | -768,575 | 7040,150 | |||
| -8,160 | 66,586 | -543,338 | 4433,642 | |||
| -7,160 | 51,266 | -367,062 | 2628,162 | |||
| -6,160 | 37,946 | -233,745 | 1439,869 | |||
| -6,160 | 37,946 | -233,745 | 1439,869 | |||
| -4,160 | 17,306 | -71,991 | 299,484 | |||
| -4,160 | 17,306 | -71,991 | 299,484 | |||
| -1,160 | 1,346 | -1,561 | 1,811 | |||
| 0,840 | 0,706 | 0,593 | 0,498 | |||
| 0,840 | 0,706 | 0,593 | 0,498 | |||
| 0,840 | 0,706 | 0,593 | 0,498 | |||
| 4,840 | 23,426 | 113,380 | 548,759 | |||
| 6,840 | 46,786 | 320,014 | 2188,892 | |||
| 6,840 | 46,786 | 320,014 | 2188,892 | |||
| 6,840 | 46,786 | 320,014 | 2188,892 | |||
| 6,840 | 46,786 | 320,014 | 2188,892 | |||
| 8,840 | 78,146 | 690,807 | 6106,735 | |||
| 9,840 | 96,826 | 952,764 | 9375,197 | |||
| 11,840 | 140,186 | 1659,798 | 19652,002 | |||
| 12,840 | 164,866 | 2116,874 | 27180,666 | |||
| 12,840 | 164,866 | 2116,874 | 27180,666 | |||
| 13,840 | 191,546 | 2650,991 | 36689,717 | |||
| 13,840 | 191,546 | 2650,991 | 36689,717 | |||
| 15,840 | 250,906 | 3974,345 | 62953,620 | |||
| 18,840 | 354,946 | 6687,175 | 125986,379 | |||
| 22,840 | 521,666 | 11914,842 | 272134,998 | |||
| 23,840 | 568,346 | 13549,359 | 323016,721 | |||
| 24,840 | 617,026 | 15326,916 | 380720,591 | |||
| 25,840 | 667,706 | 17253,513 | 445830,768 | |||
| 26,840 | 720,386 | 19335,150 | 518955,413 | |||
| 27,840 | 775,066 | 21577,826 | 600726,684 | |||
| 30,840 | 951,106 | 29332,097 | 904601,862 | |||
| 32,840 | 1078,466 | 35416,810 | 1163088,050 | |||
| 55,840 | 3118,106 | 174115,017 | 9722582,533 | |||
| Итого | 21562,720 | 41605,690 | 25342680,292 |
2) Найдем размах выборки  = = 183-85 = 98 у.е.
= = 183-85 = 98 у.е.
3) Вычислим длину интервала  =
=  = 14.
= 14.
4) Границы интервалов:
 = 85,
= 85,  = 85+14 = 99,
= 85+14 = 99,
 = 99+14 = 113,
= 99+14 = 113, 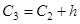 = 113+14 = 127,
= 113+14 = 127,
 = 127+14= 141,
= 127+14= 141,  = 141+14 = 155,
= 141+14 = 155,  = 155+14= 169,
= 155+14= 169,  =169 +14 =183
=169 +14 =183  .
.
5) Построим интервальный статистический ряд:
Таблица 1.2 – Интервальный статистический ряд
Границы интервалов
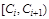 , у.е. , у.е.
| Частоты

| Частости

|
| [85, 99] | 4/50 | |
| (99, 113] | 9/50 | |
| (113,127 ] | 11/50 | |
| (127, 141] | 16/50 | |
| (141, 155] | 7/50 | |
| (155, 169] | 2/50 | |
| (169, 183] | 1/50 | |
| итого |
6) Вычислим числовые характеристики.
В качестве оценки математического ожидания используется среднее арифметическое 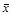 наблюденных значений. Эта статистика называется выборочным средним.
наблюденных значений. Эта статистика называется выборочным средним.
 .
.
По интервальному статистическому ряду определяется модальный интервал, в который попало наибольшее число элементов выборки, и в качестве точечной оценки моды может использоваться среднее значение этого интервала.
 .
.
Для определения выборочного значения медианы используется вариационный ряд. В нашем случае объем выборки  = 50 – четное число, т.е. в качестве оценки медианы примем
= 50 – четное число, т.е. в качестве оценки медианы примем
 =
=  .
.
В качестве оценки дисперсии используется статистика  =
=  .
.
Оценка среднего квадратического отклонения
 =
=  .
.
Оценка коэффициента вариации  .
.
Оценка коэффициента асимметрии  .
.
Оценка коэффициента эксцесса
 .
.
7) Построим гистограмму частот.

Рисунок 1.3 – Гистограмма частот
8) Построим интервальные оценки для неизвестных истинных значений  и
и  .
.
Объем выборки составил n = 50. Требуется с доверительной вероятностью  определить интервальные оценки:
определить интервальные оценки:
а) для средней стоимости строительно-монтажных работ на участке;
б) для дисперсии стоимости строительно-монтажных работ на участке;
в) для среднего квадратического отклонения стоимости строительно-монтажных работ на участке.
а) Средняя стоимость строительно-монтажных работ на участке характеризуется генеральной средней a. Требуется найти интервальную оценку  параметра a с доверительной вероятностью
параметра a с доверительной вероятностью  .
.
Применяем формулу
 ,
,
где  ,
,  ,
,  ,
,  , значение
, значение  определяем по таблицам распределения Стьюдента для
определяем по таблицам распределения Стьюдента для  и
и 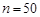 .
.  . Подставим найденные значения в формулу:
. Подставим найденные значения в формулу:

 у.е.
у.е.
Таким образом, с вероятностью  можно гарантировать, что средняя стоимость строительно-монтажных работ на участке находится в пределах:
можно гарантировать, что средняя стоимость строительно-монтажных работ на участке находится в пределах:  .
.
б) определим интервальную оценку для дисперсии стоимости строительно-монтажных работ на участке.
Интервальная оценка дисперсии
 .
.
По таблице процентных точек  -распределения (см. приложение Г) найдем
-распределения (см. приложение Г) найдем
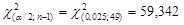 ;
;
 .
.
Следовательно,  .
.
Значит с доверительной вероятностью  можно утверждать, что истинное значение дисперсии будет находиться в интервале
можно утверждать, что истинное значение дисперсии будет находиться в интервале

в) С доверительной вероятностью  можно утверждать, что истинное значение среднего квадратического отклонения s будет находиться в интервале
можно утверждать, что истинное значение среднего квадратического отклонения s будет находиться в интервале

7) Произведем первичную обработку полученной выборки с помощью ЭВМ:
Summary Statistics for Col_1
| Count | |
| Average | 127,16 |
| Median | 128,0 |
| Mode | 134,0 |
| Variance | 440,056 |
| Standard deviation | 20,9775 |
| Coeff. of variation | 16,4969% |
| Minimum | 85,0 |
| Maximum | 183,0 |
| Range | 98,0 |
| Stnd. skewness | 0,276588 |
| Stnd. kurtosis | -0,251092 |


Рисунок 1.4 – Компьютерный расчет






