Количество информации.
Существует несколько подходов к измерению информации. Выделим два из них.
Алфавитный (технический) подход.
В технике информацией, как правило, считается любая последовательность знаков или символов. Для определения количества такой информации подсчитывают длину такой последовательности (сообщения), без учёта её содержательной части.
Определение. Информационным объёмом сообщения называется количество двоичных символов, которое используется для кодирования этого сообщения.
Пусть М – количество символов (мощность) алфавита, в котором записано сообщение, N — количество символов в записи сообщения. Тогда информационный объём сообщения
I=N•log2М (1)
Если 1оg2 М не является целым числом, то его нужно округлить в большую сторону или найти значение log2 М1, где М1 — ближайшая целая степень 2, М1 > М.
Информационный объём сообщения, выраженный в битах, и минимальное количество разрядов, необходимое для записи сообщения в двоичном алфавите, совпадают.
С помощью n двоичных разрядов можно закодировать двоичным кодом все элементы множества мощностью 2. Информационный объём одного символа алфавита, обозначающего элемент данного множества, равен n.
Пример 1. Определите информационный объём слова «разряд», если считать, что алфавит состоит из 10 букв.
Решение. Длина данного сообщения равна 6, мощность алфавита равна 10. По формуле (1) находим I = 6*log2 10. Так как число 10 не является целой степенью числа 2, то значение log210 необходимо округлить в большую сторону или найти значение log2 М, где М — ближайшая целая степень числа 2, М > 10. Следовательно, М=16. Тогда I=6*1og216 = 6*4 = 24бита.
Ответ: 24.
Пример 2. Какое количество информации необходимо для кодирования каждого символа из 256 символов некоторого алфавита?
Решение. По формуле (1) находим I = 1*log2 256 = 8 битов.
Ответ: 8 битов.
В вычислительной технике используются две стандартные единицы измерения информации: бит и байт.
Определение. Бит — минимальная единица количества информации, равная одному двоичному разряду.
Определение. Байт — единица количества информации, являющаяся наименьшей единицей памяти компьютера и равная 8 битам.
Для больших объёмов информации используют производные единицы измерения:
1 б (байт) = 8 бит (8 двоичных разрядов).
1 Кб (килобайт) = 210 б = 1024 б.
1 Мб (мегабайт) = 220 б = 1024 Кб.
1 Гб (гигабайт) = 230 б = 1024 Мб.
1 Тб (терабайт) = 240 б = 1024 Гб.
1 Пб (петабайт) = 250 б = 1024 Тб.
Вероятностный подход.
Определение. Количество информации можно рассматривать как меру уменьшения неопределённости знания при получении информационных сообщений.
За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределённость знания в два раза. Такая единица названа битом.
Пусть N — общее число возможных исходов какого-то процесса, и из них интересующее нас событие может произойти К раз. Тогда вероятность этого события равна К/N. Вероятность выражается в долях единицы
Количество информации для событий с различными вероятностями определяется по формуле:
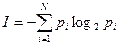 (2)
(2)
где I — количество информации, N — количество возможных событий, р — вероятности отдельных событий.
Если события равновероятны, то количество информации определяется по формуле
I = log2 N (3)
или из уравнения
N = 2 i (4)
Пример 1. В корзине лежат 8 мячей разного цвета (красный, синий, жёлтый, зелёный, оранжевый, фиолетовый, белый, коричневый). Какое количество информации несёт в себе сообщение о том, что из корзины будет вынут мяч красного цвета?
Решение. Так как возможности вынуть мяч каждого из возможных цветов равновероятны, то для определения количества информации, содержащейся в сообщении о выпадении мяча красного цвета, воспользуемся формулой (3): I = lоg2 N = lоg2 8 = 3 (бита).
Ответ: 3 бита.
Пример 2. В корзине лежат 16 мячей разного цвета: 4 красных, 8 синих, 4 жёлтых. Какое количество информации несёт в себе сообщение о том, что из корзины извлечён один мяч?
Решение. Так как количество мячей различны х цветов неодинаково, то вероятности зрительных сообщений о цвете вынутого мяча различны. Для определения этих вероятностей разделим количество мячей одного цвета на общее количество мячей. Получим вероятность вынуть мяч: красного цвета - рк = 4/16 = 0,25; синего цвета - рс = 8/16 = 0.5; жёлтого цвета - рж = 4/16 = 0,25.
Так как события не являются равновероятными, то воспользуемся формулой (1):
I = - (рк*lоg2 рк + рс*lоg2 рс + рж*log2 рж) =(0,25*log20,25 + 0,5*log20.5 + 0,25*log2 0,25) =-(2*0,25*(-2) + 0,5*(-1)) = 1,5 (бита).
Ответ: 1,5 бита.
Количество информации, содержащейся в алфавитном сообщении
Если алфавит состоит из N символов, то количество информации, которое несёт один символ, можно определить по формуле (2) или в случае, если считать, что появление каждого символа события равновероятные, - по формулам (3-4).
Чтобы определить количество информации, содержащейся в сообщении, записанном в некотором алфавите, следует количество информации, которое несёт в себе один символ этого алфавита, умножить на число символов в сообщении.
Пример. Известно, что объём сообщения составляет 3 Кб. Определить мощность алфавита, с помощью которого записано это сообщение, если известно, что оно содержит 3072 символа.
Решение. Объём данного сообщения равен 3 Кб = 3 * 1024 * 8 бит = 24576 бит. Тогда на один символ приходится 24576: 3072 = 3. По формуле (4) определяем количество символов в рассматриваемом алфавите: N=2I =23=8.
Ответ: 8 символов.
Представление числовой информации.
Представление чисел в памяти компьютера имеет специфическую особенность, связанную с тем, что в памяти компьютера числа должны располагаться в байтах - минимальных по размеру адресуемых ячейках памяти. Адресом числа считают адрес первого байта. В байте может содержаться произвольный код из восьми двоичных разрядов.
1. Целые числа представляются в памяти компьютера с фиксированной запятой. В этом случае каждому разряду ячейки памяти компьютера соответствует один и тот же разряд числа, запятая находится справа после младшего разряда (то есть вне разрядной сетки).
Для кодирования целых чисел от 0 до 255 достаточно иметь 8 разрядов двоичного кода (8 бит).
| Десятичное число | Двоичный код |
| о | |
| 1111 1110 | |
| 1111 1111 |
Для кодирования целых чисел от 0 до 65 535 требуется шестнадцать бит; 24 бита позволяют закодировать более 16,5 миллионов разных значений.
Если для представления целого числа в памяти компьютера отведено N бит, то количество различных значений будет равно 2N.
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках стоят единицы. Если под представление целого положительного числа отведено N бит, то максимальное значение будет равно 2N - 1.
Прямой код целого числа может быть получен следующим образом: число переводится в двоичную систему счисления, а затем его двоичную запись слева дополняют необходимым количеством незначащих нулей, соответствующим количеству незаполненных разрядов, отведённых для хранения числа.
2. Для представления целых чисел со знаком старший (левый) разряд отводится под знак числа. Если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то - 1.
Максимальное значение целого числа со знаком достигается в случае, когда в старшем разряде стоит 0, а во всех остальных ячейках стоят единицы. Если под представление целого числа со знаком отведено N бит, то максимальное значение будет равно 2N-1 - 1. Поскольку количество возможных значений в N битах равно 2N - 1, то в случае представления целых чисел со знаком количество отрицательных значений на единицу больше количества положительных значений. Такая ситуация связана с тем, что для представления нуля во всех ячейках стоят нули. Если же в знаковом разряде стоит единица, а во всех остальных разрядах - нули, то это представление соответствует отрицательному (как правило, наименьшему) числу.
Пример. Запишем вид числа -58 в памяти компьютера в 8-разрядном представлении.
Так как 581о = 1110102, то число в памяти компьютера будет представлено следующим образом:
Представление в памяти компьютера целых положительных чисел совпадает с прямым кодом.
З. Другой способ представления целых чисел - дополнительный код.
Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:
1) записываем прямой код модуля числа;
2) инвертируем его (заменяем единицы нулями, нули единицами);
3) прибавляем к инверсному коду единицу.
Пример. Запишем дополнительный код числа —58 в 8-разрядном представлении.
1) Прямой код числа 58 есть 00111010; 2) инверсный (обратный) код 11000101; 3) дополнительный код 11000110.
4. При получении числа по его дополнительному коду необходимо определить его знак. Если число окажется положительным, то переводим его код в десятичную систему счисления.
В случае отрицательного числа необходимо выполнить следующий алгоритм:
1) вычитаем из кода числа 1;
2) инвертируем код;
3) переводим в десятичную систему счисления;
4) полученное число записываем со знаком минус.
Пример 1. Запишем число, соответствующее дополнительному коду 00110110.
Так как в старшем разряде данного числа нуль, то результат будет положительным. После перевода числа из двоичной системы счисления в десятичную получаем 54.
Пример 2. Запишем число, соответствующее дополнительному коду 10110110.
Так как в старшем разряде данного числа единица, то результат будет отрицательным. Вычитаем из кода единицу: 10110110 — 1 = 10110101. Инвертируем код: 01001010. Переводим в десятичную систему счисления 010010102 = 7410. Полученное число записываем со знаком минус: —7410.






