Практическое занятие 7. Матрицы
Вопросы для повторения
1. Транспонирования матриц.
2. Операции сложения и вычитания матриц.
3. Операции умножения и возведения в степень матриц.
4. Понятие обратной матрицы.
Задача 74.
Найти сумму матриц:
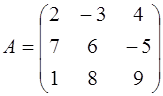 ,
,  .
.
Решение:
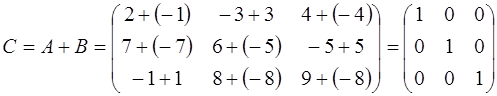 .
.
Задача 75.
Даны три матрицы:
 ,
,  ,
,  .
.
Найти матрицу  .
.
Решение:
 ,
, 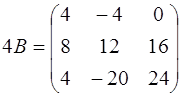 ,
, 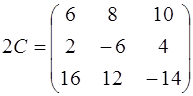 .
.
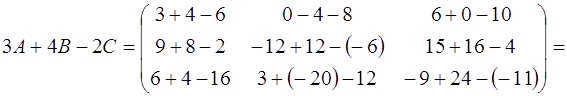
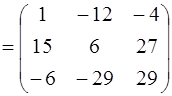 .
.
Задача 76.
Найти произведение матриц 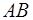 и
и  :
:
1.  ,
,  ;
;
2. 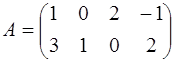 ,
,  ;
;
3.  ,
,  .
.
Ответ:
1. 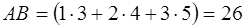 ,
,  ;
;
2. 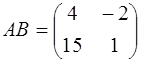 ,
,  ;
;
3. 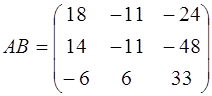 ,
,  .
.
Способ нахождения обратной матрицы
Пусть 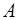 – невырожденная матрица. Припишем к ней справа (или слева) единичную матрицу
– невырожденная матрица. Припишем к ней справа (или слева) единичную матрицу  . Далее с помощью элементарных преобразований над строками сдвоенной матрицы
. Далее с помощью элементарных преобразований над строками сдвоенной матрицы  левая половина приводится к единичной матрице. Тогда сдвоенная матрица приобретает вид
левая половина приводится к единичной матрице. Тогда сдвоенная матрица приобретает вид 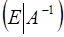 .
.
Задача 77.
Для матрицы 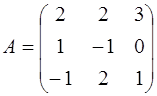 найти обратную матрицу
найти обратную матрицу  и проверить равенство
и проверить равенство  .
.
Решение:
При описанном выше способе нет необходимости специально проверять невырожденность матрицы 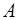 . Это будет вытекать из самой возможности приведения
. Это будет вытекать из самой возможности приведения 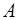 к
к  .
.
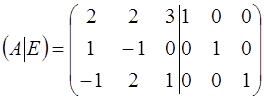

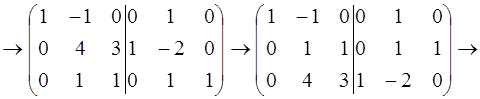


Практическое занятие 8. Определитель и ранг матрицы
Вопросы для повторения
1. Определитель  - го порядка.
- го порядка.
2. Свойства определителей.
3. Правила нахождения определителей  - го порядка.
- го порядка.
4. Понятие ранга матрицы.
Определитель матрицы третьего порядка вычисляется следующим образом:
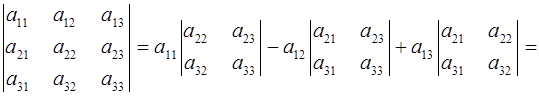
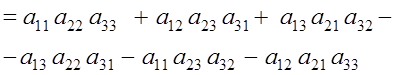
Метод Саррюса
Определитель матрицы третьего порядка представляет собой алгебраическую сумму шести слагаемых. Каждое слагаемое является произведением трех элементов, расположенных в разных столбцах и разных строках матрицы.
Знак «плюс» имеют произведение элементов, образующих треугольники со стороной, параллельной главной диагонали.
Знак «минус» имеют произведение элементов, принадлежащих побочной диагонали, и два произведения элементов, образующих треугольники со стороной, параллельной побочной диагонали.
С помощью формул разложения определителя матрицы по элементам строки или столбца вычисление определителя матрицы любого порядка сводится к вычислению определителей матриц второго или третьего порядков.
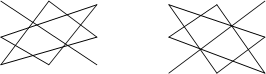

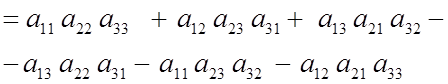
Задача 78.
Упростить выражение:  .
.
Решение: 
Задача 79.
Решить уравнение:  .
.
Решение:
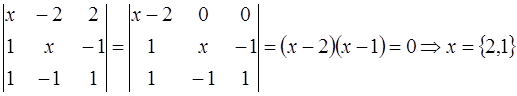 .
.
Задача 80.
Вычислить определитель:  .
.
Решение:
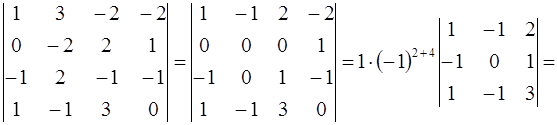
 .
.
Задача 81.
Для данной матрицы 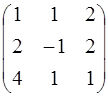 найти обратную
найти обратную
1. методом исключения:
2. методом присоединенной матрицы.
Решение:
1. 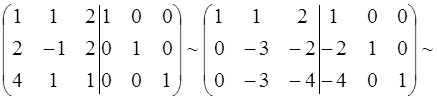

 ;
;
2.  ;
;  .
.
Задача 82.
Решить матичное уравнение 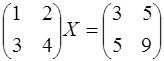
1. методом исключения;
2. методом обратной матрицы.
Решение:
1. 
 ;
;
2. Введем обозначение  , тогда уравнение запишется в виде
, тогда уравнение запишется в виде 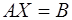 . Умножив слева это уравнение на обратную матрицу
. Умножив слева это уравнение на обратную матрицу  , которая существует, поскольку
, которая существует, поскольку 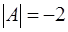 .
.
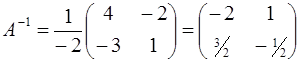 .
.
Тогда  .
.
Задача 83.
Вычислить определитель третьего порядка  .
.
Решение:
Используя формулу Саррюса, получим:
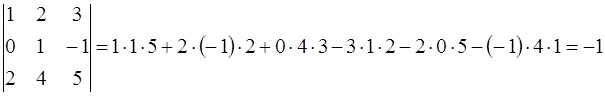 .
.
Задача 84.
Найти ранг матрицы методом элементарных преобразований:
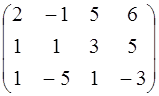 .
.
Решение:
Приведем матрицу к ступенчатому виду с помощью элементарных преобразований:

Полученная матрица содержит две ненулевые строки, значит, ее ранг равен 2. Следовательно, ранг исходной матрицы также равен 2.
Задача 85.
Найти ранг матрицы методом окаймляющих миноров и указать один из базисных миноров  .
.
Решение:
Так как у матрицы A есть ненулевые элементы, то 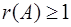 . Найдем какой-либо ненулевой минор 2-го порядка (если он существует). Таким минором является, например
. Найдем какой-либо ненулевой минор 2-го порядка (если он существует). Таким минором является, например  .
.
Значит, 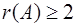 . Вычислим миноры третьего порядка, окаймляющие
. Вычислим миноры третьего порядка, окаймляющие 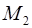 :
:
 ;
;

Все миноры 3-го порядка, окаймляющие 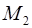 , равны нулю, следовательно
, равны нулю, следовательно  . Итак,
. Итак, 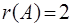 .
.
Одним из базисных миноров является 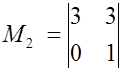 .
.
Практическое занятие 9. Многочлены
Вопросы для повторения
1. Сложение и умножение многочленов.
2. Теорема о делении с остатком.
3. Понятие корня многочлена.
4. Понятие кратности корня многочлена.
5. Схема Горнера.
6. Соотношение степени многочлена и числа его корней.
7. Разложение правильной рациональной дроби на простейшие.
8. Метод неопределенных коэффициентов.
Задача 86.
Выполнить деление с остатком 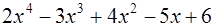 на
на  .
.
Решение:
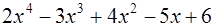
| 
| |||
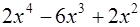
|   
| |||
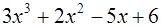
| ||||

| ||||

| ||||
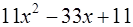
| ||||

| ||||
Задача 87.
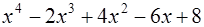 на
на 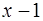 .
.
Решение:
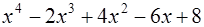
| 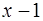
| |||
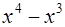
|  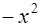  
| |||

| ||||
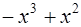
| ||||
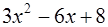
| ||||
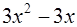
| ||||

| ||||

| ||||
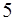
| ||||
Задача 88.
 на
на  .
.
Ответ: (Частное  , остаток
, остаток 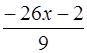 ).
).
Задача 89.
 на
на  .
.
Ответ:  .
.
Задача 90.
При каком условии полином 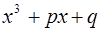 делится на полином
делится на полином  .
.
Ответ: 
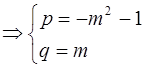 .
.
Задача 91.
При каком условии полином  делится на полином
делится на полином  .
.
Ответ:
Если 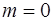 , то
, то 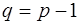 ; если
; если 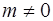 , то
, то 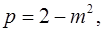
 .
.
Схема Горнера
Пусть  .
.
Если  , то коэффициенты многочлена
, то коэффициенты многочлена  и
и  проще всего найти по схеме Горнера.
проще всего найти по схеме Горнера.
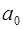
| 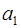
| 
| 
| 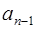
| 
| |
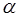
| 
| 
| 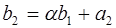
| 
| 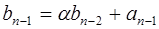
| 
|

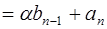
Задача 92.
Пользуясь схемой Горнера вычислить  .
.
 ,
,  .
.
Ответ:
| -3 | -10 | ||||
 .
.
Задача 93.
Пользуясь схемой Горнера вычислить  .
.
 ,
,  .
.
Ответ:
| -3 | -4 | ||||
| -1 | -4 |
 .
.
Задача 94.
Пользуясь схемой Горнера вычислить 
 ,
,  .
.
Ответ:
| -8 | -50 | ||||
| -4 | -18 |
 .
.
Задача 95.
Пользуясь схемой Горнера вычислить 
 ,
,  .
.
Ответ:
 .
.
Задача 96.
Разложить на простейшие дроби  .
.
Ответ:  .
.
Задача 97.
Разложить на простейшие дроби  .
.
Ответ: 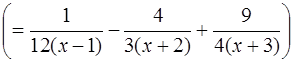 .
.
Задача 98.
Разложить на простейшие дроби 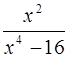 .
.
Ответ:  .
.
Задача 99.
Разложить на простейшие дроби (не вычисляя коэффициентов)  .
.
Ответ:
 .
.
Задача 100.
Разложить на простейшие дроби (не вычисляя коэффициентов)  .
.
Ответ: 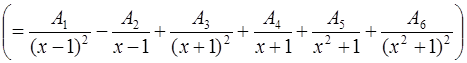 .
.




