Рассмотрим установившейся режим в системе, которая обладает равномерно распределенными линейными параметрами. Задача, связанная с анализом подобных систем, возникает, как только длительности сигналов оказываются настолько малыми (а частоты столь высокими), что длина электромагнитной волны становиться соизмерима с линейными размерами систем. Для того, чтобы показать основное отличие данного класса задач от задач анализа электрических цепей с сосредоточенными постоянными и не слишком усложнять математическую трактовку рассмотрим однородную линию передачи сигналов. Конкретно это может быть двухпроводная линия, коаксиальны кабель и т.п. Подобную систему характеризуют четыре постоянные погонные параметра, т.е. параметры, отнесенные к единицам длины: 1) последовательное линейное сопротивление 
, Ом/м; 2) параллельная проводимость (проводимость утечки между проводами) Gn, См/м; 3) последовательная индуктивность 
, Гн/м; 4)параллельная емкость между проводами 
, Ф/м.
Напряжение и ток в линии являются теперь функциями двух независимых переменных: пространственной координаты x, определяющей место наблюдения сигнала, и времени t, определяющего момент наблюдения. Направление координатной оси выбирается совпадающим с направлением линии и отсчитываемым от ее начала. Задача анализа заключается в нахождении пространственно–временного распределения тока в линии 
и напряжения между проводами 
Расчетная схема элементарного участка линии показана на рис.30 а.
Пусть 
и 
есть напряжение и ток в линии в точке с координатой x в момент t, тогда в точке с координатой (
) в тот же момент времени значения этих перменных (с точностью до бесконечно малых величин высших порядков, чем 
) будут равны:
Из закона Ома для этого участка изменение напряжения равно
т.е. 
Аналогично (или из свойства дуальности) изменение тока на этом участке равно
Полученные уравнения образуют систему двух уравнений с частными производными первого порядка. Из них легко исключить любую неизвестную функцию путем частного дифиринцирования одного уравнения по x, а второго по t. После решения новой системы уравнений можно получить два телеграфных уравнения:
описывающих электромагнитные процессы в длинной линии, Уравнения относятся к классу гиперболических уравнений математической физики, для их решения требуется задание как начальных, так и граничных условий для напряжения и тока. Для установившегося режима уравнение (94) превращается в обыкновенное дифиринциальное уравнение. Например, для установившегося синусоидального режима из уравнения, перейдя к комплексным изображениям, получим
откуда, после преобразований, находим
и из выражения аналогично определяем
Если обозначить через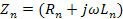 
комплексное сопротивление линии на единицу длины, а через 
– комплексную проводимость на единицу длины, то уравнения примут вид
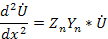
и
Разумеется, в общем случае, здесь величина 
, а связана с постоянной распространения
В установившемся синусоидальном режиме уравнения также превращаются в обыкновенные дифференциальные уравнения:
Для конечных приращений эта система в соответствии со схемой на рис.30 б, примет вид
Кроме того, надо учесть, что нагрузкой данного элемента служит характеристическое сопротивление линии ZO, поэтому систему (104) надо дополнить уравнением 
.
Сигнальный граф в соответствии с полученной системой для отрезка линии передачи показан на рис.30 в. Из сигнального графа находим
Определим характеристическое сопротивление 
, Ом, как сопротивление линии в точке, бесконечно удаленной от приемного конца.
Поскольку входное сопротивление 
должно равняться характеристическому (волновому) Z0, из формулы (106) найдем
В случае распределенной механической системы – механической длинной линии с распределенной на единицу длины массой mn=m/l, податливостью (обрат упругости) Cn=Cm/l и потерями Gn=Gm/l – система будет представлять бесконечную цепочку из указанных элементов (рис.31 а). Переходя к механической моделирующей цепи (рис. 31 б) и к электрической модели(рис.31 в) и затем к дуальной цепи, получим длинную линию (рис.31 г) без сопротивления проводов Rn=0. Из уравнения для электрической длинной линии при Rn=0, заменяя i=dq/dt, найдем
где 
скорость распространения электромагнитных волн в линии.
Используя электромеханическую аналогию (табл. 5), из последнего уравнения, приняв 
где η – коэффициент вязкости среды;
E – модуль Юнга среды;
S – площадь поперечного сечения, получим волновое уравнение для линейной вязкоупругой среды, описываемой реологической моделью Максвелла, дополненной элементом инерции (массы):
где 
- фазовая скорость волны;
ξ – смещение частиц в волне.
Аналогично можно рассмотреть не продольные, а сдвиговые колебания и волны в линейных вязкоупругих средах. Проведенный анализ показывает, что реологические одномерные задачи линейной вязкоупругой среды сводятся к задачам линейных электрических цепей с сосредоточенными или распределенными постоянными, в случае волнованных задач известные реологические модели следует дополнить элементом массы (аналогично тому, как это сделано для модели Максвелла на рис.31 а)
Механические (акустические) линии на ультразвуковых частотах совместно с пьезо-или магнитно-стрикционными преобразователями часто используют как элементы временной задержки (линии задержки) электрических сигналов.
ЛИТЕРАТУРА
1. Электротехника. /Под ред. Герасимова В.Г. М.: Высшая школа, 1965. 480с.
2. Теоретические основы электротехники. /Под ред. П.А.Ионкина. T.I. М.: Высшая школа, 1976. 544с.
3. Норенков И.Л. Введение в автоматизированное проектирование технических устройств и систем. М.: Высшая школа, 1980. 320с.
4. Чуа Л.О., Пен-Мин Лин. Машинный анализ электронных схем. М.: Энергия, 1980. 640с.
5. Тетельбаум И.М., Тетельбаум Я.И. Модели прямой аналогии. М.: Наука, 1979. 383с.
6. Крон Г. Тензорный анализ сетей. М.: Советское радио, 1978. 719с.
