Исходные данные для силового расчета

 

Исходные данные были взяты из расчетов раздела 1 для значения углового положения ведущего звена φ₁=90^◦. Данные представлены в таблице 2.1.

Таблица 2.1

№пп	Параметр	Обозначение	Размерность	Значение
	Угловая координата кривошипа	φ1	град
	Угловая скорость кривошипа	ω1	рад/с	26,376
	Длина кривошипа ОА	lOA	м	0,3
	Длина шатуна АВ	lВА	м	1,5
	Длина кривошипа ОС	lOC	м	0,12
	Длина шатуна CD	lCD	м	0,6
	Движущая сила	Fд	кН	78,3
	Приведенный суммарный момент сил движущих и сил сопротивления	МпрΣ	кН*м	20,1
	Приведенный момент сил сопротивления	МпрС	кН*м	33,5
	Теоретический приведенный момент движущих сил	Мд.теор	кН*м	13,4
	Приведенный суммарный момент инерции	JпрΣ	кг*м2
	Приведенный момент инерции первой группы звеньев	JпрI	кг*м2
	Момент инерции звена 2	JS2	кг*м2
	Момент инерции звена 4	JS4	кг*м2	3.5
	Масса коленчатого вала с маховиком	m1+ mмах	кг
	Масса шатуна АВ	m2	кг
	Масса шатуна CD	m4	кг
	Масса нижнего поршня 3	m3	кг
	Масса верхнего поршня 6	m6	кг
	Масса тяги DE(D’E’)	m5, m5’	кг

 

Построение планов скоростей и ускорений

2.2.1 Построение планов скоростей

 

Масштаб плана скоростей:

Линейная скорость точки Aзвена 1найдена по формуле для вращательного дви­жения

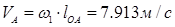
где V_А – скорость точки А,

ω₁ – угловая скорость звена 1,

l_OA – длина кривошипа ОА.

Для нахождения скорости точки Взвена 3составим векторное уравнение сложного движения:

где V_B – скорость точки В,

V_ВА – скорость точки В относительно точки А.

Из графического решения этого уравнения установлены значения скорости

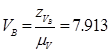м/c

м/c

где z_VBA – длина вектора скорости V_BA в масштабе μ_V,

z_VB – длина вектора скорости V_B в масштабе μ_V.

Угловая скорость звена 2 определена из формулы для вращательного движения

где l _BA – длина шатуна ВА.

Скорость точки S₂ определена пропорциональным делением отрезков плана скоростей:

мм

м/с

где l_AS2 – длина отрезка AS₂,

z_VS2 - длина вектора скорости V_S2 в масштабе μ_V.

Линейная скорость точки Сзвена 1найдена по формуле для вращательного дви­жения

где V_С – скорость точки С,

ω₁ – угловая скорость звена 1,

l_OС – длина кривошипа ОС.

Для нахождения скорости точки Dзвена 5составим векторное уравнение сложного движения:

где V_D – скорость точки D,

V_DC – скорость точки D относительно точки C.

Из графического решения этого уравнения установлены значения скорости

м/c

м/c

где z_VDC – длина вектора скорости V_DC в масштабе μ_V,

z_VD – длина вектора скорости V_D в масштабе μ_V.

Угловая скорость звена 4 определена из формулы для вращательного движения

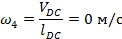
где l_DC – длина шатуна DC.

Скорость точки S₄ определена пропорциональным делением отрезков плана скоростей:

мм

м/с

где l_CS4 – длина отрезка CS₄,

z_VS4 - длина вектора скорости V_S4 в масштабе μ_V.

Все расчеты проводились при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 2.

 

 

2.2.2 Построение планов ускорений

 

Масштаб плана ускорений:

Угловое ускорение звена 1 определено из соотношения

где ε₁ – угловое ускорение звена 1,

М_прΣ – приведенный суммарный момент сил движущих и сил сопротивления,

I_прΣ – приведенный суммарный момент инерции движущихся звеньев механизма.

Ускорение точки А определено путем разложения на составляющие по взаимно перпендикулярным направления:

где aⁿ_A=l_OA*ω₁² =208.708 м/с² – нормальная составляющая ускорения точки А,

a^t_A=l_OA*ε₁ =1,035 м/с² – тангенсальная составляющая ускорения точки А.

Ускорение точки В определено из векторного уравнения

где a_B – ускорение точки В,

aⁿ_BA = l_BA*ω₂² =0м/с² – нормальная составляющая ускорения точки В относительно точки А,

a^t_BA – тангенсальная составляющая ускорения точки В относительно точки А.

Угловое ускорение звена 2 определено из формулы для вращательного движения

где ε₂ – угловое ускорение звена 2.

Ускорение точки С определено путем разложения на составляющие по взаимно перпендикулярным направления:

где aⁿ_C=l_OC*ω₁² =83.483 м/с² – нормальная составляющая ускорения точки C,

a^t_C=l_OC*ε₁ =0,414 м/с² – тангенсальная составляющая ускорения точки C.

Ускорение точки D определено из векторного уравнения

где a_D – ускорение точки В,

aⁿ_DC= l_CD*ω₄² =0 м/с² – нормальная составляющая ускорения точки В относительно точки А,

a^t_BA – тангенсальная составляющая ускорения точки В относительно точки А.

Угловое ускорение звена 4 определено из формулы для вращательного движения

где ε₄ – угловое ускорение звена 4.

Ускорение точки S₂ определено из векторного уравнения

где a_S2 – ускорение точки S₂,

aⁿ_S2A = l_AS2*ω₂² =0 м/с² – нормальная составляющая ускорения точки S₂ относительно точки А,

a^t_S2A = l_AS2*ε₂ =71.111 м/с² – тангенсальная составляющая ускорения точки S₂ относительно точки А.

Ускорение точки S₄ определено из векторного уравнения

где a_S4 – ускорение точки S₄,

aⁿ_S4C = l_CS4*ω₄² =0 м/с² – нормальная составляющая ускорения точки S₂ относительно точки А,

a^t_S4C=l_CS4*ε₄ =28.398 м/с² – тангенсальная составляющая ускорения точки S₂ относительно точки А.

Все расчеты проводились при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 2.

 

 

2.3 Расчет нагрузок, приложенных к механизму

Вследствие ускоренного движения звеньев механизма, к ним приложены силы и моменты инерции.

где G_i –сила тяжести i-го звена,

Ф_i – равнодействующая сил инерции i-го звена,

M_ФSi – главный момент сил инерции относительно центра тяжести i-го звена.

Все расчеты проведены при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 2.

Результаты вычислений приведены в таблице 5.

Таблица 5

G1, кН	G2, кН	G3, кН	G4, кН	G5, кН	G6, кН	ФS2, кН	ФS4, кН	ФB, кН	Ф5, кН	Ф6, кН	MФS1, кН*м	MФS2, кН*м	MФS4, кН*м
	2,5	2,3		2,8	3,0	35,08	5,7	9,66	4,887	5,236	19,533	7,111	0,993

2.4 Определение реакций в кинематических парах

Для нахождения неизвестных силовых факторов были использованы методы кинетостатики.

2.4.1 Расчет группы звеньев 2-3

 

Из схемы группы звеньев 2-3 механизма в масштабе μ_l=100мм/м были определены плечи сил относительно точки А.

Для определения силы F₃₀ была записана сумма моментов для группы звеньев 2-3 относительно точки А.

 

где – сила, с которой звено 0 действует на звено 3,

– плечо силы F₃₀ относительно точки А,

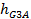– плечо силы G₃ относительно точки А,

– плечо силы G₂ относительно точки А,

– плечо силы Ф_S2 относительно точки А.

Для определения силы F₂₁ было записано векторное уравнение сил для группы звеньев 2-3. Решение уравнения производилось графически.

где F₂₁ – сила, с которой звено 1 действует на звено 2.

Для определения силы F₃₂ было записано векторное уравнение сил для звена 3. Решение уравнения производилось графически.

где F₃₂ – сила, с которой звено 2 действует на звено 3.

Все расчеты проведены при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 2.

 

2.4.2 Расчет группы звеньев 4-6

 

Из схемы группы звеньев 4-6 механизма в масштабе μ_l=100мм/м были определены плечи сил относительно точки С.

Для определения силы F₆₀ была записана сумма моментов для группы звеньев 4-6 относительно точки C.

 

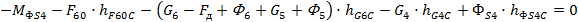
где – сила, с которой звено 0 действует на звено 6,

– плечо силы F₆₀ относительно точки C,

– плечо силы G₆ относительно точки C,

– плечо силы G₄ относительно точки C,

– плечо силы Ф_S4 относительно точки C.

Для определения силы F₄₁ было записано векторное уравнение сил для группы звеньев 4-6. Решение уравнения производилось графически.

где F₄₁ – сила, с которой звено 1 действует на звено 4.

Для определения силы F₆₅ было записано векторное уравнение сил для звена 6. Решение уравнения производилось графически.

где F₆₅ – сила, с которой звено 5 действует на звено 6.

Для определения силы F₄₅ было записано векторное уравнение сил для группы звена 4. Решение уравнения производилось графически.

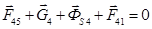
где F₄₅ – сила, с которой звено 5 действует на звено 4.

Все расчеты проведены при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 2.

 

2.4.3 Расчет звена 1

 

Из схемы звена 1 механизма в масштабе μ_l=100мм/м были определены плечи сил относительно точки О.

Для определения момента сопротивления М_с была записана сумма моментов для звена 1 относительно точки О.

 

где – движущий момент,

– сила, с которой звено 2 действует на звено 1,

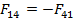– сила, с которой звено 4 действует на звено 1,

– плечо силы F₁₂ относительно точки O,

– плечо силы F₁₄ относительно точки O.

Для определения силы F₁₀ было записано векторное уравнение сил для звена 1. Решение уравнения производилось графически.

где F₁₀ – сила, с которой звено 0 действует на звено 1.

Была определена относительная погрешность между моментами сопротивления определенными графически и аналитически.

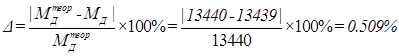
Все расчеты проведены при помощи программы Mathcad. Расчет и результаты расчетов представлены в Приложении 2.

 

 

 

3. ПРОЕКТИРОВАНИЕ ЗУБЧАТОЙ ПЕРЕДАЧИ И ПЛАНЕТАРНОГО МЕХАНИЗМА РЕВЕРC-РЕДУКТОРА СИЛОВОЙ СУДОВОЙ УСТАНОВКИ

 

3.1 Исходные данные

Число зубьев колеса Z₅: Z₅=10.

Модуль колес Z₅ и Z₆: m₅₆=10мм.

Частота оборотов коленчатого вала: n₁=25/6 рад/c.

Частота оборотов гребного вала: n₁₀=125/6 рад/с.

Модуль зубчатых колес планетарного реверс-редуктора: m_п.р.=8мм.

Число сателлитов планетарного реверс-редуктора: k=3.

Зубчатые колеса – цилиндрические, зубья – прямые (β=0 – угол наклона зубьев).

Данные по ГОСТ 13755-81 исходного производящего контура:

- Угол главного профиля a=20^◦;

- Коэффициент высоты головки зуба h_a^*=1;

- Коэффициент высоты ножки зуба h_f^*=1.25;

- Коэффициент граничной высоты h_l^*=2h_a^*=2;

- Коэффициент радиуса кривизны исходной прямой ρ_f^*=0.44;

- Коэффициент радиального зазора c^*=0.25.

 

3.2 Проектирование зубчатой передачи

 

3.2.1 Расчет параметров исходного производящего контура

 

Угол профиля:

Шаг:

Модуль зубьев:

Коэффициент высоты головки зуба:

Коэффициент радиального зазора:

Ширина впадин по делительной прямой:

Толщина зубьев по делительной прямой:

Радиус скругления основания ножки зуба:

 

3.2.2 Расчет параметров зубчатых колес

 

Передаточное отношение одноступенчатого редуктора:

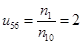
Число зубьев колеса Z₆:

Радиус делительной окружности колеса Z₅:

Радиус делительной окружности колеса Z₆:

Радиус основной окружности колеса Z₅:

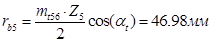
Радиус основной окружности колеса Z₆:

Наименьшее число зубьев без смещения, свободных от подрезания:

 

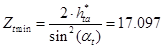
Коэффициент наименьшего смещения исходного контура:

Для определения оптимального смещения исходного производящего контура были рассчитаны параметры зубчатых колес и качественные показатели зубчатой передачи. Смещение x₅ изменялось в пределах от 0,1 до 1,4 с шагом 0,1. Смещение x₆ было принято постоянным и равным

Расчеты производились при помощи программ Mathcad и ZUB. Расчеты представлены в приложении 3. Результаты расчетов представлены в таблице 5.

По данным ГОСТ 16532-81 для кинематической передачи с числом зубьев 10<Z₅<30 и Z₆<30 были выбраны смещения исходного производящего контура

 

3.2.3 Построение профиля зуба колеса, изготавливаемого реечным инструментом

 

Профиль зуба изготовляемого колеса образуется как огибающая ряда положений исходного производящего контура реечного инструмента в станочном зацеплении. При этом эвольвентная часть профиля зуба образуется прямолинейной частью реечного производящего контура, а переходная кривая профиля зуба – закругленным участком.

Процесс построения процесс построения производился поэтапно:

1) были проведены делительная и основная 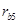окружности, окружности вершин и впадин .

2) от делительной окружности (с учетом знака) было отложено выбранное смещение и проведена делительная прямая исходного производящего контура реечного инструмента. На расстоянии вверх и вниз от делительной прямой были проведены прямые граничных точек, а на расстоянии - прямые вершин и впадин. Станочно-начальная прямая была проведена касательной к делительной окружности в точке (полюс станочного зацепления).

3) была проведена линия станочного зацепления через полюс станочного зацепления касательно к основной окружности в точке , которая образует с прямыми исходного производящего контура инструмента углы .

4) был построен исходный производящий контур реечного зацепления инструмента так, чтобы ось симметрии впадин совпадала с вертикалью, для этого от точки пересечения вертикали с делительной прямой (точки G) было отложено влево по горизонтали отрезок в 1/4 шага и через его конец перпендикулярно линии зацепления проведена наклонная прямая, которая образует угол с вертикалью. Эта прямая является прямолинейной частью зуба исходного производящего контура инструмента. Закругленный участок профиля был построен как сопряжение прямолинейной части контура с прямой вершин или с прямой впадин двумя окружностями радиуса .

Симметрично относительно вертикали был построен профиль второго зуба исходного производящего контура. Расстояние между одноименными профилями зубьев исходного контура равно шагу .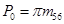

5) Строится профиль зуба проектируемого колеса, касающегося профиля исходного производящего контура в точке К.

Для построения ряда последовательных положений профиля зуба исходного производящего контура была проведена вспомогательная прямая ММ касательно к окружности вершин. Была зафиксирована точка пересечения линии ММ и прямолинейной части профиля инструмента W и центр окружности закругленного участка профиля – точка L. На прямой ММ было отложено несколько отрезков равной длины и отмечаются точки I, II, III,..., XIII. Такие же по величине отрезки были отложены на станочно-начальной прямой Q-Q (точки 1, 2, 3, …, 13) и на дуге делительной окружности (точки ). Из центра колеса через точки на делительной окружности проводятся лучи до пересечения с окружностью вершин в точках . При перекатывании без скольжения станочно-начальной прямой по делительной окружности, точки 1, 2, 3,…, 13 и точки последовательно совпадают, то же происходит для точек I,II,III … и . При этом точка W описывает укороченную эвольвенту, а точка L – удлиненную.

Любое промежуточное положение точки W или L было найдено методом засечек. Для положения 2 выбран треугольник II-2-W, размеры которого при обкатке сохраняются. Когда точка 2 совпадает с точкой , сторона II-2 проходит по лучу и занимает положение стороны . Тогда точка определяется как положение вершины треугольника, построенного методом засечек по известным сторонам ; ; , т.е. треугольник займет положение треугольника . Аналогично было найдено положение точки . Из точки радиусом проведена окружность, а через точку касательно к этой окружности – прямая, которая дает новое (второе) положение исходного производящего контура. Все последующие положения были построены аналогично. К полученному ряду положений профиля зуба исходного контура была проведена огибающая, которая определяет левый профиль зуба изготовляемого колеса. Правый профиль зуба был построен с помощью зеркального отображения левого профиля относительно вертикальной прямой совпадающей с осью симметрии исходного производящего контура. Копируя полученный профиль, на колесе были построены три зуба. Для этого откладываются от вертикали в обе стороны шаги по хорде делительной окружности .Через концы этих отрезков и центр колеса проведены линии симметрии правого и левого зубьев, по отношению к которым по шаблону были построены зубья колеса.

3.2.4 Построение проектируемой зубчатой передачи.

 

Проектируемая зубчатая передача строилась поэтапно:

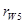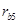1) было отложено межосевое расстояние и проведены окружности: начальные и ; делительные и и основные и ; окружности вершин и впадин 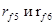. Начальные окружности касаются в полюсе зацепления. Расстояние между делительными окружностями по осевой линии равно воспринимаемому смещению . Расстояние между окружностями вершин одного колеса и впадин другого, измеренного по осевой линии, должно быть равно радиальному зазору .

2) через полюс зацепления касательно к основным окружностям была проведена линия зацепления. Точки касания и - предельные точки линии зацепления, которая образует с перпендикуляром, восстановленным к осевой линии в полюсе, угол зацепления . Точками и 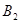отмечена активная линия зацепления. Точка является точкой пересечения окружности вершин колеса с линией зацепления, а точка 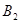является точкой пересечения окружности вершин шестерни с линией зацепления.

3) профили зубьев построены так, чтобы точка контакта К располагалась на активной линии зацепления. Профиль шестерни были получены соответствующим поворотом зубьев, полученных в станочном зацеплении. Эвольвентная часть профиля колеса была построена, как траектория точки прямой при перекатывании ее по основной окружности колеса без скольжения и перенесена в точку контакта зубьев К на линию зацепления. Поскольку и , то эвольвентную часть была сопряжена с окружностью впадин радиусом . Профили других зубьев расположены на расстоянии шага . Нижние точки активных профилей лежат на пересечении окружностей и соответствующих профилей.

 

3.3 Проектирование планетарного механизма реверс-редуктора

 

Был дана схема планетарного редуктора с двумя внешними зацеплениями. При кинематическом синтезе многосателлитной планетарной передачи заданной схемы была решена задача подбора чисел зубьев колес, которые будут удовлетворять следующим условиям:

- выполнение заданного передаточного отношения;

- отсутствия заклинивания передачи, среза и подреза профилей зубьев колес;

- соосность входного и выходного валов;

- соседства;

- сборки.

Для данного двухрядного планетарного механизма с двумя внешними зацеплениями передаточное отношение вычисляется по формуле:

где U^H₄₁ – передаточное отношение планетарного редуктора при остановленном водиле Н.

Условие соосности имеет вид:

где r_Wi – радиус начальной окружности зубчатого колеса Z_i.

Зубчатые колеса планетарного редуктора были приняты без смещения, т.е. r_i=r_Wi. Из чего получено:

где r_i – радиус делительной окружности зубчатого колеса Z_i.

Учитывая, что r_i=m*Z_i/2, было получено условие соосности, выраженное через количество зубьев колес Z_i:

Условие соседства:

где k – количество сателлитов.

Условие сборки:

где p – целое число от 1 до 10,

Ц – целое число.

Для определения чисел зубьев использовался метод простых сомножителей.

 

1)Для a=1, c=1, b=2, d=1, q=9 получено:

2) Для a=1, c=2, b=1, d=4, q=9 получено: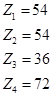

 

Выберем вариант 1) т.к. он наиболее подходящий, в силу своих геометрических размеров и полного удовлетворения всем необходимым условиям проектирования планетарных редукторов.

Радиусы делительных окружностей для полученных чисел зубьев колес:

Для графического определения передаточного отношения редуктора (метод профессора Смирнова) была вычерчена схема планетарного редуктора в масштабе μ_l=250мм/м.

Для построения прямой распределения скоростей точек звена необходимо знать скорость двух точек. Для звена 1 это точки O и A: ось O неподвижна, и ее скорость равна нулю. Скорость точки A направлена по касательной к колесу Z₁. Вектор скорости точки A изображается отрезком AA', направление которого совпадает с вектором скорости . Прямая OA' образует угол y₁ с вертикалью и является линией распределения скоростей точек на радиусе колеса Z₁. Колесо Z₄ является неподвижным и через точку C проходит ось мгновенного вращения блока сателлита Z₂-Z₃. Прямая CA' образует угол y₂₃ с вертикалью и является линией распределения скоростей точек блока сателлитов. Скорость оси B блока колес выражается отрезком ВВ'. Прямая ВВ' является линией распределения скоростей точек водила и образует угол y_Н с вертикалью.

Передаточное отношение планетарной передачи находится на основе выполненных графических построений по соотношению:

;

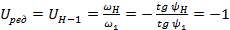Передаточное отношение редуктора верное.

Все расчеты производились при помощи программы Mathcad. Расчеты и результаты расчетов представлены в Приложении 3.

Результаты проектирования зубчатой передачи сведены в таблицу 2:

		m, мм
		10.0	0.5	0.5	27.193	0.847	158.47	1.15	2.606	0.934	0.621	0.47	0.67

 

Результаты проектирования планетарной передачи сведены в таблицу 3:

-1