Гфункцияның жабайы қасиеттері.

ИНСТИТУТЫ

Жаратылыстану факультеті.

Физика-математика кафедрасы

КУРСТЫҚ ЖҰМЫС

 

Тақырыбы: Эйлер интегралдары.

Пәні: Математикалық талдау

Мамандығы: 5В010900- Математика

Орындаған: Иса И.

Қабылдаған: доцент Абдрахманов Қ.

Комиссия мүшелері: _____________________________

 

_____________________________

 

_____________________________

 

 

Шымкент 2016

Ф 7.02-19 курстық жұмыс

 

Оңтүстік Қазақстан мемлекеттік педагогикалық институты

Жаратылыстану факультеті.

БЕКІТЕМІН

Кафедра меңгерушісі

Кадирбаева Р.И

«____»__________20__ж.

Студенттің курстық жұмысына берілетін

ТАПСЫРМА

1.Эйлер интегралдары.

2.Жұмыстың аяқталу уақыты: «29»қараша 2016 ж.

3.Жұмыстың мазмұны (Эйлердің бірінші және екінші текті интегралы,олардың қасиеттері,есептер шығару, қорытынды)

Кіріспе

I.Эйлердің бірінші текті интегралы.

II.Эйлердің екінші текті интегралы, олардың қасиеттері.

Қорытынды.

Пайдаланған әдебиеттер тізімі. 1. Фихтенгольц Г.М., Математикалық анализ негіздері, II-том, Алматы, Мектеп 1972,440б. 2.Ибрашев Х.И., Еркеғұлов Ш.Т Математикалық анализ курсы, II-том,Алматы,Мектеп 1970,527 б.

4. Кестелік және графикалық материалдардың тізімі: 1

5.Әдебиеттер тізімі:5

6.Тапсырманың берілген уақыты: 10.10. 2016ж.

7.Курстық жұмыстың жетекшісі: Абдрахманов Қ.

8.Тапсырманы алған студент: Иса Индира Бақытқызы.

 

 

Ф 7.02-19 курстық жұмыс

 

Мазмұны

 

Кіріспе….................................................................................................................4

І-тарау. Эйлердің бірінші текті интегралы..........................................................6

 

1.1.Алмастыруды, бөлшектеп интегралдауды, басқа аналитикалық өрнекпен көрсетуді қолдану...................................................................................................6

ІІ –тарау. Эйлердің екінші текті интегралы, олардың қасиеттері...............................................................................................................9

2.1 Гамма функцияның қасиеттері.....................................................................10

2.2.Екі шекті алмастыру жөнінде тарихи ескертулер.......................................17

III-тарау. Есептер...............................................................................................21

Қорытынды..........................................................................................................24

 

Пайдаланылған әдебиеттер...............................................................................25

Кіріспе.

Эйлер Леонард (Euler Leonhard) 1707 - 1783 математик, философ, физик.

Эйлер интегралдары – (бірінші текті Эйлер интегралдары не бета-функция) және (екінші текті Эйлер интегралдары не гамма-функция) түріндегі интегралдар. Бұл интегралдар француз математигі А.Лежандрдың ұсынысы бойынша Эйлер интегралдары деп аталған.

IX – XV-ғасырларда Орта және Таяу Шығыс ғалымдары Архимед еңбектерін араб тіліне аударып, ежелгі математиканың табыстарын кейінгі ұрпақтарға жеткізді. Бірақ оларды одан әрі дамыта алмады. Тек XVI – XVII-ғасырларда ғана табиғаттану ғылымдарының жетістіктері интегралдық есептеудің одан әрі дамуын қажет етті. Интегралдық есептеудің негізгі ұғымдары мен идеялық жүйесін бір-біріне тәуелсіз түрде Исаак Ньютон мен Готфрид Лейбниц жасады. «Интегралдық есептеу» термині мен интеграл таңбасы Лейбництен бастап қолданылып келеді. Интегралдық есептеудің әрі қарай дамуы швейцариялық математик Иоганн Бернуллидің, әсіресе, Леонард Эйлердің есімдерімен тығыз байланысты.XIX-ғасырдың басында француз математигі Огюстен Луи Коши шектер теориясы негізінде интегралдық есептеу мен дифференциалдық есептеуді қайта құрды. Интегралдық есептеуді дамытуға XIX-ғасырда орыс ғалымдары Михаил Остроградский, Виктор Буняковский және Пафнутий Чебышев үлкен үлес қосты. XIX-ғасырдың аяғында және XX-ғасырдың басында жиын теориясының дамуы интегралдық есептеудің негізгі ұғымдарының тереңдеуіне және кеңеюіне себеп болды.

XVI тарау («Функциялық тізбектер және қатарлар») ең алдымен осы қарастырылып отырған типті тап осы мәселелерге арналған болатын. Ондағы зерттелген мәселелері: шектеусіз қатарды қосындылау операциясын дағдылы шекке көшумен алмастыруға болатындығының,дифференициалдаудың, және интегралдаудың шарттары зерттелген.Ақырында осы тараудың негізгі мазмұны жөнінде де осыны айтуға болады; жалғыз-ақ бұл жолы алмастыратын екі операцияның біреуі ылғи интегралдау операциясы болып отырады. Оны біз белгілі шарттар орындалғанда басқа шектік операциялармен алмастырып отырдық.Осы қарастырылып отырған операциялардың «шектік» операциялар екендігін жете түсінуден көп бұрын мұндай екі операцияны алмастыру математикалық практикаға кеңінен енген. Тіпті анализдің негізін салушылардың өздері іс жүзінде қолданған. Ньютонның, Лейбництің және олардың замандастары қолданған мүшелеп дифференциалдау үшін «Лейбниц ережесін» еске түсірейік. Осындай алмастыруды XVIII ғасыр бойы қолданып келгенін көреміз. Онда көбінесе оның орындылығы дәлелденбеген, ал кейде дәлелденген болса, оның дәлдігі сол тұстағы түсінікке сәйкес қана болған. Мысал үшін екі дифференциалдауды алмастыруды дәлелдегендегі (1739ж) Эйлер мен Клероның пайымдауларын еске түсіреміз. Математикалық анализ тарихында екі шектік операцияны алмастрыу тәсілі көптеген жалпы қабылдауларды және жеке математикалық фактілерді тауып алу үшін өте күшті құрал деп табылған. Бірақ теріс қолданғандықтан, оның өзі қате мен парадокстардың көзі болған. Екі шектік операцияны алмастыру ылғи дұрыс бола бермейтіндігі туралы пікірдің өзі қателерді зерттеу негізінде барып айқындалған. Тек XIX ғасырдың орта кезінде ғана жалпының игілігіне айналған. Мұндай алмстыру кездесетін анализдің әдеткі жағдайлары үшін оның дұрыстығының дәл дәлелдемесі ғасырдың аяқ кезінде аяқталған. Бәрінен бұрын екі шектік көшуді алмастыру мәселесі айқын шешілген. XVIII және XIX ғасырдың өліарасында (15) теңдіктің кейде дұрыс болмай шығатындығы жай мысалдармен көрсетілген, яғни қайталанған шек кейде көшу ретінде тәуелді болатындығы көрсетілген. 1815 жылғы Кошидің бір мақаласында (1827 ж. жарияланған) осы мәселе дұрыс және жүйелі баяндалған.

Егер интеграл астындағы функция үзілісті болса (мысалы, шексіздікке айналатын болса), онда қайталанған интегралда интегралдау ретін сөзсіз өзгертуге болмайтындығы, Коши сияқты, Гауссқа да белгілі болған. Бірақ бұдан екі шектік операцияны жалпы алмастыру мәселесінің айқындалмағанын байқаймыз.Үздіксіз функциялардан құрылған қатардың қосындысының үздіксіздігін және осындай қатарды мүшелеп интегралдауға болатындығын дәлелдемек болып Коши жасаған әрекеттің сәтсіз аяқталғанын жоғарыда ескерткен болатынбыз. Бұл пікірдің алдыңғысының теріс екенін Абель бірден көрсеткен, ал екіншісіне кейінірек Чебышёв қарсы болды. Бұрын айтылғандарға енді мынаны қосамыз: 1823 ж. Коши интегралды параметр бойынша дифференциялдауға қатысты «Лейбниц ережесін сөзсіз қолдануға болатындығының сондай теріс дәлелдемесін берген. Бұл тұста ол ереженің қолданылуға болмайтындығын анық көрсететін мысалдардың ешқайсысын да ескермеген. Интеграл астындағы функция шексіздікке айналатын жағдайда интеграл астында дифференциялдау мүмкін болмай қалатындығын Остроградский 1828 ж анық түсінген. Кейінгі кезде бұл жағдайды басқа авторлар да көрсеткен.

 

ЭЙЛЕР ИНТЕГРАЛДАРЫ

1.Эйлердің бірінші текті интегралы. Интеграл(лат. іnteger – бүтін) –математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан – туындысы бойынша функцияны іздеу (мысалы, қозғалған нүктенің жүріп өткен жолын өрнектейтін функцияны сол нүктенің жылдамдығы бойынша табу), екінші жағынан – аудан, көлем және доға ұзындығын өлшеу, күштің белгілі бір уақыт ішінде атқарған жұмысын табу, т.б. қажеттіліктерден пайда болды. Осыған қатысты интеграл анықталмаған интеграл және анықталған интеграл болып ажыратылады. Міне, осыларды есептеу интегралдық есептеудің міндеті болып саналады. «Интеграл» сөзін алғаш рет (1690) швейцариялық ғалым Якоб Бернулли қолданған.Интеграл анықтамасын басқаша өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама деп те атай аламыз.

Эйлердің бірінші текті интегралы (Лежандрдың ұсынысы бойынша) мына түрдегі

(1)

 

интеграл осылай аталады, мұнда a,b 0. Бұл интеграл а және b айнымалы параметрлердің В («Бета») функциясы болады.

Бұл қарастырылып отырған интеграл a және b- нің оң мәндерінде (кемінде бірден кіші мәндеріне) жинақты ) болатынын бұрыннан білеміз. Сондықтан, расында оны В функцияны анықтауға негіз етіп алуға болады. Осы функцияның қасиеттерін анықтайық.

1.1. Алдымен, тікелей дерлік (х=1-t алмастыруды қолданып)

теңдікті тауып аламыз. Сол себепті В функция a және b –ге қатысты симмЕнді Г функцияның пайдаланылуы жөнінен бірнеше жай мысалдар келтіреміз.

 

Бөлшектеп интегралдауды қолданып, (1) формуладан b 1 болғанда мынаны табамыз

 

Осыдан мына формула табылады:

(2)

b саны 1-ден артық болып қалып отырғанда оны кеміту үшін осы формуланы қолдануға болады. Сонымен қашанда екінші аргумент ≤1 болатындай етуге болады.

Алайда, осы айтылғанды бірінші аргумент жөнінде де істеуге болады. В симметриялы функция болғандықтан, басқа келтіру формуласы да болады:

(2)

Егер b натурал санына тең болса, онда (2) формуланы біртіндеп қолданып, мынаны табамыз:

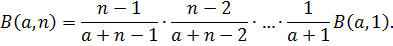
Бірақ

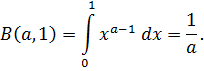
Сондықтан В және бірден В үшін де мынадай ақтық өрнек табылады

(3)

Егер a да натурал m санына тең болса, онда

 

болады. Егер 0! символды 1 деп түсінетін болсақ, бұл формуланы 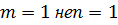болғанда да қолдануға болады.

1.3. В функциясын басқа аналитикалық өрнекпен көрсетейік. Мұның пайдасы көбірек. Егер (1) интегралда алмастыруды қолдансақ, онда

(4)

болады. Мұндағы y-0- ден -ке дейін өзгертіп жаңа айнымалы. Мұнда b=1-a деп алып (0< a <1 деп ұйғарып), табатынымыз

Бұл интеграл бұрын есептелінген және Эйлердің есімімен байланысты аталады, оны оқушы байқаған болу керек. Бұның мәнін орнына қойып, мына формулаға келеміз

(5)

Егер, дербес жағдайда,

деп алсақ, мынаны табамыз:

«Бета» функцияның осы аздаған қасиеттерімен біз қанағаттанамыз. Себебі бұл функция тіпті жай түрде басқа «Гамма» функциямен өрнектелетіндігін төменде көреміз және ол функцияға толығырақ тоқтап өтеміз.

2.Эйлердің екінші текті интегралы. Бұл атауды Лежандр мына тамаша интегралға қойған:

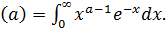(6)

Бұл интеграл кез келген a <0 болғанда жинақты және Г («Гамма») функцияны анықтайды. Г функция анализ бен оның қолданулары үшін элементар функциялардан кейінгі маңызды функцияның бірі болады. Бұның (6) интегралдық анықтамасына сүйеніп отырып, Г функцияның қасиеттерін зерттеу деген параметрге тәуелді интегралдардың жоғарыда баяндалған теориясының қолдануларының тамаша мысалы болып табылмақ.

Егер (6)-да

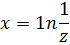
деп алсақ, онда мынаны табамыз:

*) а ≤0 болғанда интеграл жинақсыз.

 

Ал

теңдік бізге белгілі және де өрнегі өскенде өзінің шегіне өсе отырып*) ұмтылады. Мұндай жағдайда

болады немесе, егер алмастыруды қолдансақ,

 

болады. Бірақ (3) бойынша

Сонымен, ақырында, Эйлер – Гаусстың атақты формуласына келеміз:

Г

Бұл формуланы Эйлер тіпті 1729ж. Гольдбахқа жолдаған хатында жазған, бірақ кейін ұмыт болған. Ақырында бұл формуланы Гаусс ІІ (а)=Г(а+1) функциясының анықтамасына негіз етіп алады. Г функциясымен Лежандр мен Лобачевский көп шұғылданған. Және де Лобачевский ол функцияның шектеусіз қатарлар пайдаланылып берілетін анықтамасына сүйенген.

Гфункцияның жабайы қасиеттері.

1˚. Г(а)функция барлық а>0 мәндерінде үздіксіз және оның барлық ретті үздіксіз туындылары болады. Тек туындыларының бар екендігін дәлелдеу жеткілікті. (6) интегралды интеграл астында дифференциалдап,

(7)

тауып аламыз. Лейбниц ережесінің дұрыс қолданылып отырғандығын мына екі интегралдың

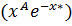а-ға қатысты бір қалыпты жинақтылығынан көреміз: біріншісі х =0 болғанда a≥a₀>0 үшін мажорантасы), ал екіншісі х= болғанда а≤А< үшін мажорантасы).

Осылайша

(7*)

екінші туындының және барлық жоғарғы туындыларының бар екендігіне көз жеткізуге болады.

2˚. (6)-ны бөлшектеп интегралдап бірден табатынымыз:

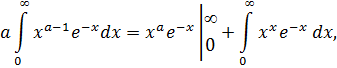
яғни

(8)

Бұл формуланы қайталап қолданғанда шығатыны

(8*)

Осы жолмен а аргументтің кез келген мәнінде Г- ны есептеуді 0<а≤1 ( не қажет болса 1<а≤2 үшін де) болғанда Г-ны есептеуге келтіруге болады.

Егер (8*)-де а=1 деп алынса және

(9)

теңдік еске алынса, онда мына теңдік табылады:

(10)

Сонымен Г функциясы тек -нің натурал мәндерінде анықталған функциясының – аргументтің, кез келген оң мәндерінің облысына табиғи қолданылуы болып шығады.

3˚. Г функцияның өзгеру жолы. Енді біз 0-ден -ке дейін а өскендегі Г (а) функциясының сипаты жөнінде жалпы түсінік бере аламыз.

(9) және (10) бойынша: Г (1)=Г (2) =1 болады. Сондықтан, Ролль теоремасы бойынша, 1-мен 2-нің арасында Г’ (а) туындының а₀ түбірі жату керек. Бұл туынды ылғи да өседі, өйткені Г” (а) екінші туындының әрқашан оң болатындығы оның (7*) өрнегінен көрініп тұр. Сөйтіп, 0<а<а₀ болғанда Г’ (а)<0 және Г (а) функциясы кемиді, ал а₀<а< болғанда Г’ (а)>0, сондықтан Г (а) өседі; а = а₀ болғанда минимум болады. Біз бұл жерде оның есептеуін келтірмейміз, тек ақырғы нәтижесін жазамыз:

а- ның 0-ге немесе ұмтылғандағы (а) функцияның шегін анықтау қызғылықты. (8) –ден (және 1˚-ден) а→0 жағдайда

 

екені айқын. Екінші жағынан, (10) бойынша, тек қана а> 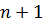болысымен, (а)> яғни а→ жағдайда болады.

Г (а) функцияның графигі 5-суретте келтірілген.

4˚. В және Г функцияларының арасындағы байланыс. Бұл байланысты анықтау үшін біз x=ty (t>0) алмастыруды қолданып, (6)-ны мына түрге түрлендіреміз:

 

 

(11)

Мұнда а- ны а+ -мен ауыстырып және сонымен бірге t-ні 1+ t- ге ауыстырып, мынаны табамыз:

Енді осы теңдіктің екі жағын 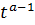-ге көбейтеміз және t бойынша 0-ден -ке дейін интегралдаймыз:

Сол жақтағы интеграл өзімізге белгілі В (a, b) функциясы [(4)-ті қараңыз]; оң жақта интегралдардың орнын алмастырамыз. Нәтижесінде [(7) және (6)-ны ескере отырып] мынаны табамыз:

Осыдан, ақырында,

(12)

өрнегі табылады.

Осы қатыста Эйлердің келтірілген әп-әсем қорытындысын Дирихле жасаған. Дегенмен, бұл қорытындыны толық дәлелді ету үшін әлі де интегралдарды алмастырудың орындылығын көрсету керек болады.

Мұны біз әуелі a>1, b>1 деп алып көрсетпекпіз. Сонда

функциясы үшін 5-теоремасының барлық шарттары орындалатын болады. Бұл функция y≥0 және t≥0 үшін үздіксіз (және де оң), ал мына интегралдар да

және

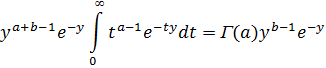
үздіксіз болады: біріншісі t≥0 үшін t –нің функциясы да, екіншісі y≥0 үшін y –тің функциясы. Теоремаға сүйенгенде интегралдардың орнын ауыстырудың, ал сонымен бірге (12) формуланың a>1, b>1 жағдайда дұрыс екендігін көреміз.

Егер де тек a>0, және b>0 белгілі болса, онда дәлелденген бойынша,

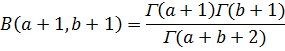
болады. Ал осыдан В функция үшін (2), (2’) келтіру формулаларын және Г функция үшін (8)-ді пайдаланып керексіз шарттарды қоймастан, қайтадан (12) формуланы табу оңай.

5˚. Толықтыру формуласы. Егер (12) формулада b=1-a десек (0< a<1 деп) онда, (5) және (9) бойынша, мына қатыс табылады

(13)

бұл толықтыру формуласы деп аталады.

Ал болғанда осыдан (Г (a)>0 себепті)

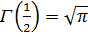(14)

формуласы шығады.

интегралда ауыстыруды орындап, біз бұрыннан белгілі интегралды қайтадан табамыз:

6˚.Лежандр формуласы. Егер

интегралда 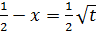ауыстыруды орындасақ, онда

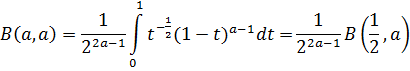
теңдігі шығады.

Екі жағдайда да В функцияны (12) өрнек бойынша Г функциямен алмастырамыз:

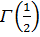Г -ға қысқартып және орнына оның мәнін қойып [(14)-ті қараңыз], Лежандр формуласына келеміз:

 

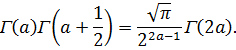
Г функциясының терең қасиеттерін ашып көрсететін көптеген басқа да формулалар бар. Бұл жерде оларға тоқтауға біздің мүмкіндігіміз жоқ. Сонымен бірге Г функцияның өзінің мәндерін және оның логарифмдерін жуық есептеу тәсілдеріне де тоқтай алмаймыз. Лежандр Г функцияның қасиеттерін және шектеусіз қатарлар аппаратын пайдаланып -ның 1-мен 2-нің арасында 0,001 аралықпен алынған мәндері үшін функцияның логарифмдерінің таблицасын алдымен 7 ондық, ал соңынан 12 ондық таңбамен жасағанын ескертіп, осыған доғарамыз.

Бұл жаңа элементтер емес, Г функция өзіміз элементар деп атап үйренген функциялар сияқты болып табылады.

Мысалдар.

Енді Г функцияның пайдаланылуы жөнінен бірнеше жай мысалдар келтіреміз.

 

1) (p,q,m>0)

интеграл ауыстыруды қолданғанда бірден Эйлердің бірінші текті интегралына келтіріледі:

2) Мына интегралды есептеп шығарайық

Егерx=sin𝜑 десек, онда мына

интегралға келеді. Алдыңғы мысалды пайдаланып, мынаны табамыз:

Дербес жағдайда, b=1 болғанда, осыдан

формуласы табылады. Осы бір формулаға (5) формуланың екеуі бірдей енетінін тексеру оңай.

Егер де бастапқы интегралда деп алсақ (мұнда ), онда толықтыру формуласын қолданып мына формуланы табамыз:

3) Ақырында мына

интегралды қарастырамыз. Мұнда p және q- өз ара жай тақ натурал сандар.

Интеграл мына түрде

қайта жазып, оған Лобачевскийдің жалпы формуласын қолданамыз. Бұл формуланың дұрыс болу шарттары

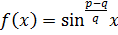
функциясы үшін орындалған. Сонымен [2)-ні қараңыз]

теңдігі табылады.

Г функциясын енгізгеннен кейін белгілі функциялар арқылы интегралдарды шектеулі түрде өрнектеу мүмкіндігінің қаншалықты кеңіп отырғандығын осы келтірілген мысалдардан –ақ оқушы айқын көріп отыр. Кейде ең ақырғы нәтижеге Г функциясы кірмегеннің өзінде де ол нәтиже осы функцияның қасиеттерін пайдаланғанда оңай табылады.

2.2 Екі шектік операцияны алмастыру жөнінде тарихи ескертулер. Бұл соңғы параграфтың көздейтін мақсаты екі шектік операцияны алмастыру жөнінде айтылғандардың бәрін тарихи мағлұмат беру тұрғысынан салғастыру болмақ. «Шектік операция» деп біз бұл жерде қарастырылып отырған функцияның бір аргументі бойынша тікелей шекке көшуді ғана емес, ақтығында осындай шекке көшуге әкеп тірейтін басқа оперцияларды да түсінетін боламыз. Ол операциялар мыналар: шектеусіз қатарды қосындылау, функцияны дифференциалдау және ақырында, тұрақты шектер аралығында функцияны интегралдау (меншікті не меншіксіз мағынада). Қайталанған екі шектің

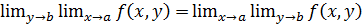(15)

өз ара теңдігі туралы сөз болған. Мұндай теңдіктің ылғи дұрыс бола бермейтінін біз көргенбіз және мұның дұрыс болуын қамтамасыз ететін кейбір шарттарды анықтағанбыз.Осыған ұқсас мәселе аралас екі туындының

(16)

өз ара теңдігі жөнінде болғанды.

XVI тарау («Функциялық тізбектер және қатарлар») ең алдымен осы қарастырылып отырған типті тап осы мәселелерге арналған болатын. Ондағы зерттелген мәселелері: шектеусіз қатарды қосындылау операциясын дағдылы шекке көшумен алмастыруға болатындығының,дифференициалдаудың, және интегралдаудың шарттары зерттелген.

Ақырында осы тараудың негізгі мазмұны жөнінде де осыны айтуға болады; жалғыз-ақ бұл жолы алмастыратын екі операцияның біреуі ылғи интегралдау операциясы болып отырады. Оны біз белгілі шарттар орындалғанда басқа шектік операциялармен алмастырып отырдық.Осы қарастырылып отырған операциялардың «шектік» операциялар екендігін жете түсінуден көп бұрын мұндай екі операцияны алмастыру математикалық практикаға кеңінен енген. Тіпті анализдің негізін салушылардың өздері іс жүзінде қолданған. Ньютонның, Лейбництің және олардың замандастары қолданған мүшелеп дифференциалдау үшін «Лейбниц ережесін» еске түсірейік. Осындай алмастыруды XVIII ғасыр бойы қолданып келгенін көреміз. Онда көбінесе оның орындылығы дәлелденбеген, ал кейде дәлелденген болса, оның дәлдігі сол тұстағы түсінікке сәйкес қана болған. Мысал үшін екі дифференциалдауды алмастыруды дәлелдегендегі (1739ж) Эйлер мен Клероның пайымдауларын еске түсіреміз. Математикалық анализ тарихында екі шектік операцияны алмастрыу тәсілі көптеген жалпы қабылдауларды және жеке математикалық фактілерді тауып алу үшін өте күшті құрал деп табылған. Бірақ теріс қолданғандықтан, оның өзі қате мен парадокстардың көзі болған. Екі шектік операцияны алмастыру ылғи дұрыс бола бермейтіндігі туралы пікірдің өзі қателерді зерттеу негізінде барып айқындалған. Тек XIX ғасырдың орта кезінде ғана жалпының игілігіне айналған. Мұндай алмстыру кездесетін анализдің әдеткі жағдайлары үшін оның дұрыстығының дәл дәлелдемесі ғасырдың аяқ кезінде аяқталған.

Бәрінен бұрын екі шектік көшуді алмастыру мәселесі айқын шешілген. XVIII және XIX ғасырдың өліарасында (15) теңдіктің кейде дұрыс болмай шығатындығы жай мысалдармен көрсетілген, яғни қайталанған шек кейде көшу ретінде тәуелді болатындығы көрсетілген. 1815 жылғы Кошидің бір мақаласында (1827 ж. жарияланған) осы мәселе дұрыс және жүйелі баяндалған.

Егер интеграл астындағы функция үзілісті болса (мысалы, шексіздікке айналатын болса), онда қайталанған интегралда интегралдау ретін сөзсіз өзгертуге болмайтындығы, Коши сияқты, Гауссқа да белгілі болған. Бірақ бұдан екі шектік операцияны жалпы алмастыру мәселесінің айқындалмағанын байқаймыз.

Үздіксіз функциялардан құрылған қатардың қосындысының үздіксіздігін және осындай қатарды мүшелеп интегралдауға болатындығын дәлелдемек болып Коши жасаған әрекеттің сәтсіз аяқталғанын жоғарыда ескерткен болатынбыз. Бұл пікірдің алдыңғысының теріс екенін Абель бірден көрсеткен, ал екіншісіне кейінірек Чебышёв қарсы болды. Бұрын айтылғандарға енді мынаны қосамыз: 1823 ж. Коши интегралды параметр бойынша дифференциялдауға қатысты «Лейбниц ережесін сөзсіз қолдануға болатындығының сондай теріс дәлелдемесін берген. Бұл тұста ол ереженің қолданылуға болмайтындығын анық көрсететін мысалдардың ешқайсысын да ескермеген. Интеграл астындағы функция шексіздікке айналатын жағдайда интеграл астында дифференциялдау мүмкін болмай қалатындығын Остроградский 1828 ж анық түсінген. Кейінгі кезде бұл жағдайды басқа авторлар да көрсеткен.

Шектеусіз аздардың анализі бойынша оқу нұсқаларында қырқыншы жылдарға дейін осы қарастырылған мәселелерге қатысты теріс пікірлер жиі кездесіп келді. Осыған орай бұл мәселелерде сақтықтың керектігін көптеген мысалдар байқатты. Біз олардың Фурье көрсеткен тек алдыңғыларының біреуін келтіреміз:

 

Мынаның

 

 

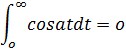
Қай типті шектік операциялар болса да алмастыру жасаудың мумкін юолу шарттарын дәл анықтау керектігі айқын анықтала бастады.Қырқыншы жылдардың аяғындаенгізілген қатардың бір қалыпты жинақтылық ұғымы және онымен түптес интегралдың бір қалыпты жинақтылық ұғымы осыны дәл анықтауға мүмкіндік туғызады.Алайда біздің осы шұғылданып отырған мселелеріміздің тиісті дәлдікпен пайымдау процесіне тағы бірнеше ондаған жылдар керек болды.Мысалы (16) формуланың бірінші дәл дәлелдемесін біз тек 1873 ж. Шварцтың еңбегінен табамыз.

түріндегі интегралы берілген болсын, бұндағы а≠ 0.

Бұл типтегі интегралдар үшін мына үш жағдай болуы мүмкін:

1˚. а >0 болған жағдай. Бұл жағдайда айнымалыны

деп ауыстырамыз. Бұны Эйлердің бірінші ауыстырмасы деп атайды. Сонда:

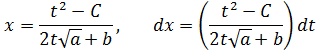
, яғни берілген айнымалыны t- нің рационалдық функцияның интегралына келеді.

 

2˚. с>0 болған жағдай. Бұл жағдайда айнымалыны

деп ауыстыру керек. Бұны Эйлердің екінші ауыстырмасы деп атайды. Осыдан х-ті және dx-ті тауып, берілген интегралдағы орындарына апарып қою керек.

3˚. квадрат үшмүшелігінің нақты түбірлері бар болсын. Сонда:

болады. Бұл жағдайда ауыстыруды

деп енгізу керек. Бұны Эйлердің үшінші ауыстырмасы деп атайды.

 

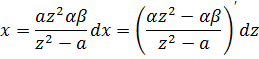
Есептер

1.

 

 

 

=

 

 

 

 

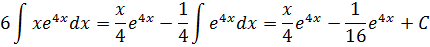
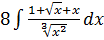анықталмаған интегралын есептеу керек.

Шешу: Интеграл астындағы бөлшекті бөліміне жеке – жеке бөліп, қатынас түрінде жазып аламыз.

 

 

 

анықталмаған интегралын есептеу керек, мұндағы а, в,с – тұрақтылар және с≠1

Шешу:

 

интегралын есептеу керек.

Шешу:

 

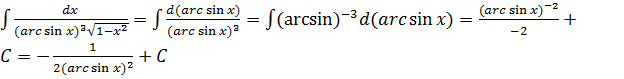
интегралын есептеу керек.

Шешу:

 

Қорытынды.

Қорыта айтқанда,Осы курстық жұмыстың мақсаты Эйлер интегралының (бірінші текті Эйлер интегралдары не бета-функция) және (екінші текті Эйлер интегралдары не гамма-функция) нақты қасиеттерін зерттеу болып табылады.Эйлер интегралын негізінен гамма функциясы,гамма функциясының зерттелген қасиеттері және бета функцияларды қамтиды.Математиканың кейбiр жеке тарауларының болсын тарихын бiлу мұғалімнің кейбiр оқушы қателiктерiн болжауына, кейде тiптi болдырмауына да жол ашады. Сонымен қатар бiраз әдiстемелiк қателiктерге жол бермеуге көмектеседi. Өз пәнiнiң тарихын жақсы бiлу, мұғалімге өтiлiп жатқан тақырып пен ұғымдардың орнын бiлiктiлiкпен бағалауға, терең бiлiм беруге көмектеседi. Егер мұғалім математиканың тарихын бiлсе, осы бiлiмiн пайдалана отырып, ол оқу үрдiсiн реттеп, математиканы оқушылар үшiн түсiнiктiрек етiп үйлестiре алады. С.П.Капица ғылым тарихының маңызы туралы былай деген: “Ғылымды оның тарихына мүлде тиiспей-ақ оқуға болатыны жақсы белгiлi. Бірақ оның тарихына бармай ғылымның әдiсiн түсiну қиын және бiздiң мәдениетiмiзден алатын орнын дұрыс анықтау мүлде мүмкiн емес”. Ғылымның тарихынан мәлiмет беру, жоғарыда айтылғандай, танымдық тұрғысынан өте пайдалы, өйткенi ол оқушыларда диалектикалық–материалистiк дүниетаным қалыптастыруға ықпал етедi. Сонымен қатар ол әр тарауды немесе тақырыпты өту барысында оқушыларға математиканың кеңiстiктiк пiшiндердiң ғылымы ретiнде адамның практикалық қызметiмен байланысты пайда болған және дамығанын көрсетуге мүмкiндiк бередi.

 

 

 

Пайдаланылған әдебиеттер тізімі:

 

1. Фихтенгольц Г.М., Математикалық анализ негіздері, II-том, Алматы, Мектеп 1972,440б.

2.Ибрашев Х.И., Еркеғұлов Ш.Т Математикалық анализ курсы, II-том,Алматы,Мектеп 1970,527 б.

3.Фихтенгольц Г.М. Дифференциялдың және интегралдың есептеу курсы. I-II том,Алматы,1970,63 бет.

4.Тілеубердиев Б. Математикалық талдау негіздері,Шымкент: «Нұрлы Бейне»,2015,291б

5. Қазақстан»: Ұлттық энцклопедия / Бас редактор Ә. Нысанбаев – Алматы «Қазақ энциклопедиясы» Бас редакциясы, 1998 ISBN 5-89800-123-9, X том;