Каждый этап задания приносит новую информацию о графике функции, поэтому в ходе решения удобно использовать своеобразный МАКЕТ. Изобразим на черновике декартову систему координат. Что уже точно известно? Во-первых, у графика нет асимптот, следовательно, прямые чертить не нужно. Во-вторых, мы знаем, как функция ведёт себя на бесконечности. Согласно проведённому анализу, нарисуем первое приближение:
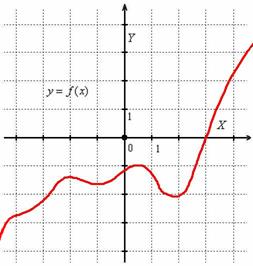
Заметьте, что в силу непрерывности функции на 
и того факта, что 
, график должен, по меньшей мере, один раз пересечь ось 
. А может быть точек пересечения несколько?
3) Нули функции и интервалы знакопостоянства.
Сначала найдём точку пересечения графика с осью ординат. Это просто. Необходимо вычислить значение функции при 
:
Полтора над уровнем моря.
Чтобы найти точки пересечения с осью 
(нули функции) требуется решить уравнение 
, и тут нас поджидает неприятный сюрприз:
В конце притаился свободный член, который существенно затрудняет задачу.
Такое уравнение имеет, как минимум, один действительный корень, и чаще всего этот корень иррационален. В худшей же сказке нас поджидают три поросёнка. Уравнение разрешимо с помощью так называемых формул Кардано, но порча бумаги сопоставима чуть ли не со всем исследованием. В этой связи разумнее устно либо на черновике попытаться подобрать хотя бы один целый корень. Проверим, не являются ли оными числа 
:
– не подходит;
– есть!
Здесь повезло. В случае неудачи можно протестировать ещё 
и 
, а если и эти числа не подошли, то шансов на выгодное решение уравнения, боюсь, очень мало. Тогда пункт исследования лучше полностью пропустить – авось станет что-нибудь понятнее на завершающем шаге, когда будут пробиваться дополнительные точки. И если таки корень (корни) явно «нехорошие», то об интервалах знакопостоянства лучше вообще скромно умолчать да поаккуратнее выполнить чертёж.
Однако у нас есть красивый корень 
, поэтому делим многочлен 
на 
без остатка:
Алгоритм деления многочлена на многочлен детально разобран в первом примере урока Сложные пределы.
В итоге левая часть исходного уравнения раскладывается в произведение:
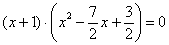
А теперь немного о здоровом образе жизни. Я, конечно же, понимаю, что квадратные уравнения нужно решать каждый день, но сегодня сделаем исключение: уравнение 
имеет два действительных корня 
.
На числовой прямой отложим найденные значения 
и методом интервалов определим знаки функции:
Таким образом, на интервалах 
график расположен
ниже оси абсцисс 
, а на интервалах 
– выше данной оси 
.
Полученные выводы позволяют детализировать наш макет, и второе приближение графика выглядит следующим образом:
Обратите внимание, что на интервале 
функция обязательно должна иметь хотя бы один максимум, а на интервале 
– хотя бы один минимум. Но сколько раз, где и когда будет «петлять» график, мы пока не знаем. К слову, функция может иметь и бесконечно много экстремумов.
4) Возрастание, убывание и экстремумы функции.
Найдём критические точки:
Данное уравнение имеет два действительных корня 
. Отложим их на числовой прямой и определим знаки производной:
Следовательно, функция возрастает на 
и убывает на 
.
В точке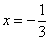 
функция достигает максимума: 
.
В точке 
функция достигает минимума: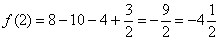 
.
Установленные факты загоняют наш шаблон в довольно жёсткие рамки:
Что и говорить, дифференциальное исчисление – штука мощная. Давайте окончательно разберёмся с формой графика:
5) Выпуклость, вогнутость и точки перегиба.
Найдём критические точки второй производной:
Определим знаки 
:
График функции является выпуклым на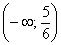 
и вогнутым на 
. Вычислим ординату точки перегиба: 
.
Практически всё прояснилось.
6) Осталось найти дополнительные точки, которые помогут точнее построить график и выполнить самопроверку. В данном случае их мало, но пренебрегать не будем:
Выполним чертёж:
Зелёным цветом отмечена точка перегиба, крестиками – дополнительные точки. График кубической функции симметричен относительно своей точки перегиба, которая всегда расположена строго посередине между максимумом и минимумом.
